4.5: Nominal GDP, Real GDP & the GDP Deflator
- Page ID
- 11806
We have discussed real GDP briefly in the beginning of this chapter, and then nominal GDP in some detail. Now we need to look carefully at both concepts and the relationship between them, which is the GDP deflator.
Nominal GDP measures output and incomes based on current market prices for goods and services and factors of production. As a result, changes in nominal GDP from one period to the next might be the result of changes in prices of final outputs and factor inputs, or the result of changes in the quantities of final outputs and factor inputs, or some combination of the two.
Since it is physical quantities of goods and services that yield satisfaction or utility, it can be misleading to judge the economy’s performance by looking at nominal GDP. For that purpose we need real GDP, as we discussed earlier in this chapter. Real GDP, or GDP in constant prices, measures the value of goods and services produced in any given year using the prices of a base year. In this way, real GDP adjusts changes in GDP for changes in prices by measuring GDP in different years in constant prices.
To illustrate this important point, Table 4.6 shows a simple economy that produces both consumer goods, blue jeans, and capital goods, solar panels. In this economy nominal GDP rises from $300,000 to $570,000 between 2000 and 2014, a 90 percent increase measured in current prices as a result of changes in both quantities and prices. If we take 2000 as the base year, we can measure real GDP in 2014 by valuing output quantities in 2014 using 2000 prices. This gives real GDP in 2014 of $525,000 in prices of the base year. In the example in the table, quantities of both products rise over the period but the price of blue jeans rises while the price of solar panels falls. As a result the rise of about 75 percent in real GDP gives a truer picture of the extra quantity of goods available in the economy in 2014 compared with 2000. It eliminates the change in GDP that was the result of the changes in prices by 8.6 percent between 2000 and 2011.
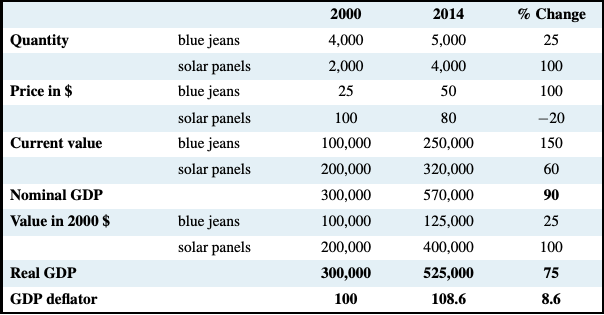
Table 4.6: Nominal and Real GDP
The GDP Deflator
The Canadian economy is obviously more complex than this economy. We have seen that GDP includes expenditures by households, governments, businesses, and residents of other countries who supply us with imports and buy our exports. To convert nominal GDP to real GDP we need to use an index that includes what is happening to the prices of all these different goods and services. This index is called the GDP deflator.
GDP deflator: index of current final output prices relative to base year prices.
If we have data for both nominal and real GDP, we can calculate the GDP deflator as the ratio of nominal GDP to real GDP expressed as an index with a value of 100 in the base year.
\[\text{GDP deflator} = \displaystyle\frac {\text{Nominal GDP}}{\text{Real GDP}} \times \:100\]
The GDP deflator differs from the consumer price index (CPI) illustrated in Example Box 4.1 and used to measure inflation in consumer prices and the cost of living. First, the CPI is based on a “representative basket” of goods and services that consumers buy, while the GDP deflator is comprehensive and covers all the goods and services included in national accounts. Second, the CPI changes over time with changes in the prices of the basket of consumer goods and services. The GDP deflator, by contrast, is built on the base year prices. It changes over time as the current prices change relative to base year prices. In other words the GDP deflator is used to “deflate” the dollar value of current 2011 output to what it would be in value would be in 2000 prices, while the CPI measures the increase in the cost of the “basket” of consumer goods and services.
But why does the GDP deflator change over time? The accounting data on nominal and real GDP do not provide an explanation. From our earlier discussion of the national income accounting framework, we can see that costs of production and net indirect taxes are include in the general level of market prices measured by the GDP deflator. Nominal GDP measured by the income approach is reported in Table 4.5. It is the sum of incomes paid to factor inputs to production, plus depreciation allowances and net indirect taxes. These components of nominal GDP are the costs of production, gross profits, and taxes that are built into the market prices of the goods and services. We can write:
Nominal GDP=employment income+profit, business, and investment income+capital consumption allowance+net indirect taxes
or
\[\text{Nominal GDP} = W + BI + CCA + T_{IN}\]
Alternatively, using the expenditure approach as illustrated in Table 4.5, using Y to denote real GDP and P for the weight average price level we have:
\[\text {Nominal GDP} = P \times \:Y = P \times (C + I + G + X - IM)\]
Our national accounting framework and procedures tell us that nominal GDP will be the same whether measured by the income approach or the expenditure approach. This means we can define the general price level as:
\[P = \displaystyle\frac {W}{Y} + \displaystyle\frac {BI + CCA}{Y} + \displaystyle\frac {T_{IN}}{Y}\]
The general price level in the economy, in accounting terms is equal to the sum of:
1. employee compensation per unit of output, W/Y;
2. gross business income per unit of output, (BI +CCA)/Y; and
3. net indirect tax per unit of output TIN/Y.
Changes in the sum of these three components of the price level must change both price and nominal GDP, whether we measure nominal GDP by the income or the expenditure approach. The GDP deflator is an index of this price level in any particular year relative to a chosen base year. However, the accounting framework does not explain the causes of change in the price level. That requires explanations of changes in unit labour costs, of producer output and pricing decisions and information on the net indirect tax rate. Those explanations are parts of an economic model of the supply side of the economy.
Now consider the empirical importance of the distinction between real and nominal GDP. Table 4.7 gives Canadian data over the period 2001 to 2013. Nominal GDP rose from 1,134.8 billion in 2001 to $1879.5 billion in 2013. Without knowing what happened to prices of goods and services in general, we cannot judge what happened to the quantity of output over that period. To answer this question we use the GDP deflator to convert nominal GDP to real GDP in the prices of the base year 2007 as follows:
\[\text{Real GDP}_{yeart} = \displaystyle\frac {\text{GDP}_t}{\text{GDP deflator}} \times \:100\]

Table 4.7: Canadian Nominal and Real GDP 2001-2013
Source: Statistics Canada CANSIM Tables 380-0064 and 380-0066 and
author's calculations.
For example, in 2013, nominal GDP was $1,879.5 billion and the GDP deflator (2007=100) was 110.9. Real GDP measured in constant 2007 dollars was then:
\(\text {Real GDP}_{2013} = \displaystyle\frac{1879.5}{110.9} \times \:100 = \text{1694.8 in 2007 dollars}\)
When converted to constant dollars, the change in real GDP is much smaller than the change in nominal GDP. Over the 2001-2013 period, real GDP increased by 26.3 percent compared to a 65.6 percent increase in nominal GDP. On average, prices in 2013 were 31.1 percent higher than in 2001. Clearly, it is important to distinguish between nominal and real GDP.


