5.3: An Economic Analysis of Charity
- Last updated
- Save as PDF
- Page ID
- 58458
The phrase "an economic analysis of" is code for "using the framework of optimization and comparative statics to study observed behavior." In this case, we use the Endowment Model from the Theory of Consumer Behavior to study charitable giving.
How can economics have anything to say about giving away money? Isn’t charity something really nice people do, not the selfish, rational maximizers that inhabit economics? Doesn’t this mean that thinking like an economist is useless for studying charity?
These questions are based on a common misunderstanding that economics applies only to a subset of the world. So, the mistaken thinking goes, you can use economics to study certain things like banking or unemployment, but not war or marriage. This is wrong because modern economics is not defined by content, but by method. Anything involving choice, like going to war or getting married or brushing your teeth or joining a church can be analyzed with the tools of economics.
We will see that the economic approach offers a different view of charitable giving. By casting the problem as a choicehow much to give is the key endogenous variablewe can apply the optimizing and comparative statics framework of economics. We do not claim this is the only or even the best perspective, but it does provide another way to understand charity.
Basic Facts about Giving
Each year, people all around the world give away a lot of money, goods, and time (as volunteers). Humans are sympathetic when people close to them are in distress. All religions encourage charity and caring for people less fortunate.
Giving USA provides data on philanthropy in the United States. Figure 5.10, from the 2018 Annual Report, shows the breakdown of the $410 billion that were contributed to charities in 2017. To help understand what this number means, we can compare total contributions to the size of the economy and we find a giving rate of about 2.1% of GDP.
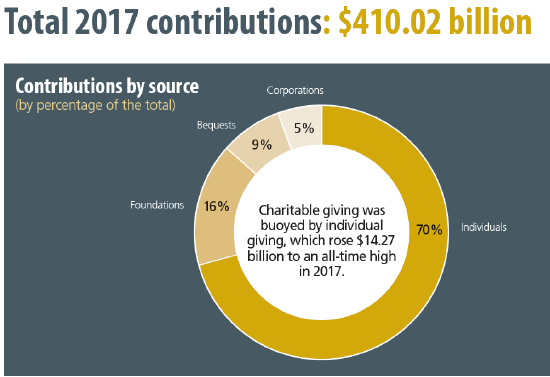
Figure 5.10: Charitable giving by source of contribution. Source: Giving USA 2018 Annual Report
The 2018 Annual Report contextualizes total giving by tracking giving over time, shown in Figure 5.11. Total giving jumped in the mid 1990s and reached its highest level in 2017. That is good news.
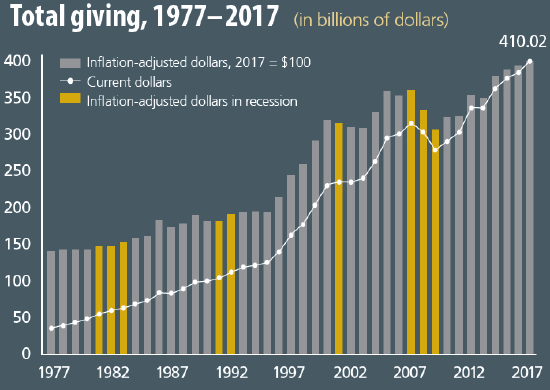
Figure 5.11: Charitable giving over time. Source: Giving USA 2018 Annual Report
The Internal Revenue Service is another source of data on charitable giving because taxpayers claim deductions when they give to charity to lower the tax owed. The IRS also collects data on non-profit organizations which do not pay tax, but they have to file Form 990. IRS data can be found at www.irs.gov/statistics.
Charitable giving data shows that it not only varies over time, there is also tremendous individual variation. Many people give nothing, others give a little, and a few people donate a lot. Religions encourage members to tithe, giving 10% of their income. Upon death, some people give substantial fractions of their estates to charity, while others hand it all to their heirs.
There are many questions we can ask about charitable giving, but our top three are:
- Why do people give to charity?
- What determines how much they give?
- How can charitable giving be stimulated?
Because this is an economic analysis of charity, we are going to answer these questions by using the method of economics. We will set up and solve an optimization problem. This will provide the economic explanation for why people give and what determines how much they give. We will see that charitable giving can be stimulated by changing exogenous variables, ceteris paribus.
Our model will do the usual stripping away of realistic details, making incredible simplifying assumptions, to enable us to solve the model and play comparative statics games. Keep your eye on the procedure as we set up, solve, and compute our key measurethe tax break elasticity of giving.
An Endowment Model of Giving
As usual, we begin with the budget constraint, then we model preferences, and we use both to find the initial solution to the problem of maximizing satisfaction subject to the budget constraint.
The optimization problem is entirely from the donor’s point of view. It is the donor, the giver, who decides how much, if any, to grant to the beneficiary, the recipient.
Figure 5.12 depicts the donor’s budget constraint in this application. The initial endowment is the coordinate pair that represents the donor’s consumption (on the y axis) and the beneficiary’s consumption (on the x axis). There is only one good (which represents consumption of all goods) and its price is $1/unit. So, if the donor has $100 and the beneficiary only $10, we know the initial endowment is at the point 10,100.
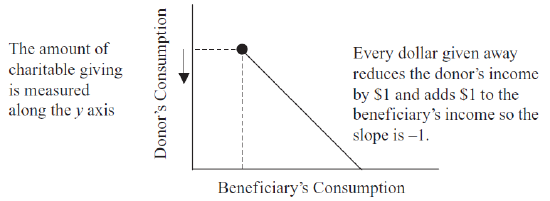 Figure 5.12: The budget constraint.
Figure 5.12: The budget constraint.Giving is modeled as moving down the budget line in Figure 5.12. If the donor gives $20 away, then she will have $80 and the beneficiary will have $30. Of course, the donor could give all of her money away, choosing to be at the x intercept. It is easy to see that the donor decides how much, if any, to give, by choosing a point on the budget line which determines both the donor’s own consumption and the beneficiary’s consumption.
Thus, at any point on the budget line, we can compute the amount of giving as simply the vertical distance (along the y axis) from the initial endowment to the point on the budget line. If the donor decides to stay on the initial endowment point, then they give nothing to the beneficiary.
The slope of the budget line is \(-1\) because there is a dollar-for-dollar exchange from the donor to the beneficiary.
Notice that this budget line does not extend left or northwest from the initial endowment because that would imply taking money from the beneficiary. The donor cannot do that.
Finally, because we will (of course) be doing comparative statics analysis, we point out that a tax break for those who donate money means that the budget line will have a shallower slope. If the donor gives $1 and is rewarded, for example, with a 30decrease in taxes, then the recipient gets $1, but the donor actually gave only 70. The slope is not \(-1\), but \(-(1 - TaxBreak)\). By adjusting the tax break, we can see how the agent responds.
This is too abstract. It is time to go to Excel to understand how the tax break really works.
STEP Open the Excel workbook Charity.xls and read the Intro sheet, then go to the MovingAround sheet.
All you see is a single point at 20,80this is the initial endowment. The donor gives nothing and there is no tax break.
STEP Change cell C5, the amount the donor gives, to 20. The beneficiary gets the 20, adding it to his initial 20, and new red dot is at 40,60. The slope of the constraint is \(-1\), displayed in I5.
Without a tax break, every dollar given is subtracted from the donor and added to the beneficiary. But the tax code incentivizes giving by lowering the donor’s tax liability.
STEP Change E5, the amount of the tax break, to 40%. The red dot jumped up. Hit ctrl-z a few times to move back forth between zero and a 40% tax break.
With or without the tax break, the beneficiary still gets 20, but a tax break on charitable donations affects how much the donor actually gave up. With a 40% tax break, the sheet shows that the donor really gave up only 12 because taxes are lowered by 8 (40% of 20). Thus, the slope of the constraint is \(-0.6\).
Wait, if the donor gives 12 and the recipient gets 20, who makes up the difference? The government. The beneficiary gets the full donation, but the donor pays less tax to the government. Clearly, by manipulating the tax break, the government can make charitable giving less expensive to donors.
So, if the tax break increases, what happens to the budget line? Think it through. You can check yourself when we get to the OptimalChoice sheet.
But before we get there, we have to consider the donor’s preferences. The constraint is only about possibilities. To know what the donor will do, we need to know the donor’s utility function.
The neat trick here is to enable the beneficiary’s consumption to affect the donor’s satisfaction. The way we model giving is to have the self-interested agent care about others.
The usual Cobb-Douglas functional form will represent the donor’s satisfaction derived from her own consumption and the beneficiary’s consumption. \[U=BeneficiaryCon^cDonorCon^d\] As usual, the exponents allow us to model different preferences. If c and d are equal, the donor gets as much satisfaction from her own consumption as the beneficiary’s consumption. She is a saint. Although possible, this is unlikely. Most people get more satisfaction from their own consumption and, thus, d is greater than c.
We will use the OptimalChoice sheet with different exponent values to see the effect on the graph, but it is worth thinking through two scenarios. What would happen to the indifference curves, starting from \(c=d\) as we lowered c? What would happen to the indifference curves if c fell all the way to zero? Again, thinking this through and testing yourself is good way to learnyou can check your answer in the OptimalChoice sheet.
It is worth remembering that preferences are not right or wrong. We take them as given and we model the agent as maximizing based on given preferences. It can be difficult to do thiswe naturally disapprove of someone who doesn’t care about others.
Another source of confusion is that preferences can and do change, but that is not to say that they are chosen by the agent. Changes to preferences are like shocks to other exogenous variablesthey are imposed by forces outside the agent’s control and then the agent re-optimizes in the new environment.
STEP Proceed to the OptimalChoice sheet to see how the donor’s optimization problem can be implemented in Excel.
The sheet shows a mathematical expression of the constrained utility maximization problem. The constraint is different than usual. If we write the constraint as an equation, we need to compute the y intercept and incorporate the fact that the donor cannot take from the recipient (the empty space in the northwest corner of Figure 5.12).
We cannot use the usual Lagrangean method to deal with this complicated constraint because it only works with equality constraints. There is an analytical method called Kuhn-Tucker that can be used, but it is beyond the scope of this book.
Fortunately, the numerical method is still available. For Excel and Solver, the complicated constraint is easily handled by adding a second constraint (cell B26) and incorporating it as an inequalitythis allows the donor to choose \(m_1\) or greater for the beneficiary. The usual budget line constraint is in cell B25. Applying both constraints gives Solver the equivalent of Figure 5.12 and it has no trouble finding the optimal solution.
Figure 5.13 shows the starting position. The endogenous variables are consumption by beneficiary and donor. These are chosen by the donor to maximize utility subject to the budget constraint.
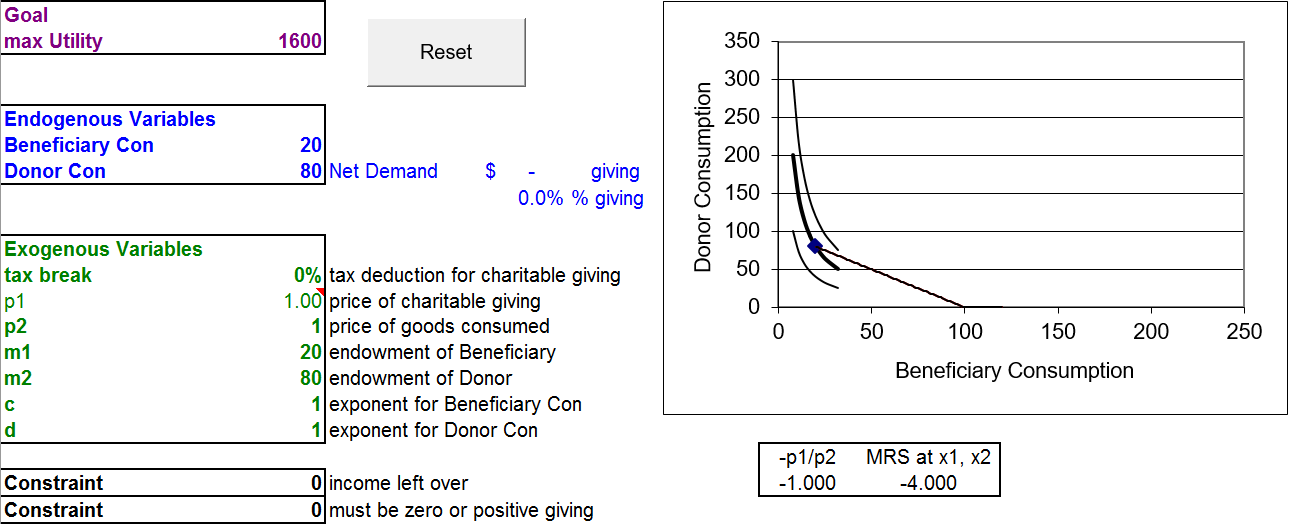
Figure 5.13: Donor with \(c=d\) opening position. Source: Charity.xls!OptimalChoice
The exogenous variables include the amount of the tax break (initially set at zero so the slope of the budget constraint is \(-1\)), prices normalized to one, the initial endowment, and the impact of donor and beneficiary consumption on the donor’s utility.
With \(c=d\), the donor cares as much about the beneficiary as herself and the MRS \(> \frac{p_1}{p_2}\) at the initial endowment. We know the donor can increase her satisfaction by traveling down the budget line. For example, suppose the agent decided to donate $10. How would this affect the chart?
STEP Change cell B11 to 30 and B12 to 70.
The MRS is now closer to the price ratio and utility has risen (from 1600 to 2100). The agent has moved down the budget line and is on a higher indifference curve.
STEP Run Solver to find the initial optimal solution.
The agent chooses the point 50,50 to maximize utility (at 2500), which means she donates $30 to the beneficiary. The net demand is the amount of giving and we express it as a dollar amount and as a percentage of the donor’s income (cell D13).
This is one mighty nice donor. She has an incredibly high giving rate of 37.5%. Because \(c = d\), she cares as much about the beneficiary as she does herself. It makes common sense that she picks an equal 50,50 split as her optimal solution.
Comparative Statics
There are several shocks to consider. We start with preferences.
STEP Change the exponent for the beneficiary’s consumption to 0.2.
This answers the earlier question about the effect of c on the indifference curves: they become much flatter as c falls, ceteris paribus. With \(c=0.2\), the donor does not care as much about the beneficiary as before.
The shape of the indifference curve is tied to the MRS. With \(c=0.2\), the MRS at 50,50 has fallen to 0.2 (in absolute value). The low MRS and flat indifference curve mean that the donor is willing to trade only a little of her consumption for a lot of additional beneficiary consumption.
The culmination of lowering c is a donor who does not care about the beneficiary at all. With \(c=0\), the indifference curves became horizontal, MRS is zero, and beneficiary consumption is a neutral good.
It is obvious that the donor with \(c=0.2\) is not going to be as generous as before when \(c=1\), but how much will they give?
STEP Run Solver. Figure 5.14 displays the result.
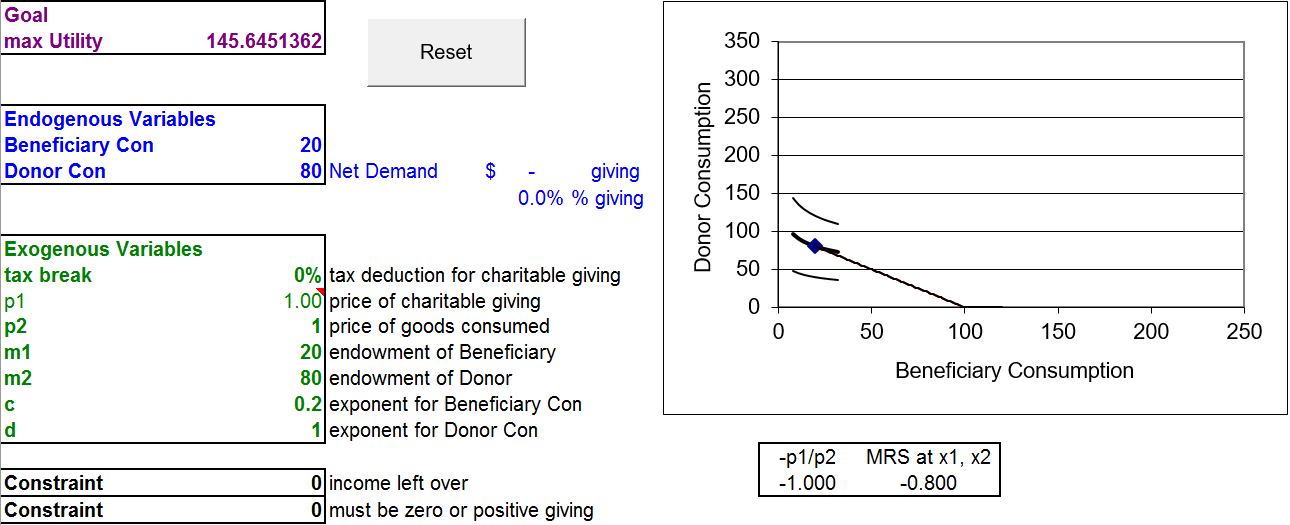
Figure 5.14: Donor with \(c=0.2\) corner solution. Source: Charity.xls!OptimalChoice
The result is a surprise. The best the agent can do is to donate nothing so that is what she does. Even though the MRS does not equal the price ratio, this donor is optimizing. This is a corner solution.
Our work thus far provides answers to two of the three questions we initially asked.
- Why do people give to charity? To maximize satisfaction. A donor gives because the consumption of others affects his or her utility. Notice that giving is perfectly compatible with self-interest. The economic model says that the donor feels good when she gives and that is why she gives.
- What determines how much they give? Clearly preferences matter. How much the donor cares about others (the exponent c in the donor’s utility function) plays a major role. Of course, the constraint also matters. Donor’s income, beneficiary’s income, and the slope of the constraint affect the amount of giving.
- How can charitable giving be stimulated?
Let’s work on the third question. We could try to convince people to care more about others, increasing c (certainly this is a primary goal of religion), but a way to stimulate giving is to lower the price of giving.
As we saw earlier, dollars given to charity reduce the donor’s taxable income and reduce tax owed. If the donor is in a 30% tax bracket, every dollar donated to charity saves the donor 30 cents in taxes. Thus, the beneficiary receives the dollar, but the donor is actually paying only 70 centswith Uncle Sam picking up the remaining 30 cents.
What effect will a 30% tax break have on the budget constraint and charitable giving of a donor with \(c=0.2\)? Apply the shock in Excel and find out.
STEP Change the tax_break variable (B16) to 30% and note that \(p_1\) becomes 0.70 and the budget line swings out.
The new red budget line is flatter than the original because of the tax break. This answers the earlier question about the effect of a tax break on the budget constraint: the bigger the tax break, the more the line swings and flattens out. This is just like lowering \(p_1\) in the Standard Model.
Notice that the MRS is greater than the slope of the new budget line. This agent can improve her utility by traveling down the constraint. This means she will donate to the beneficiary, as shown in Figure 15.15.
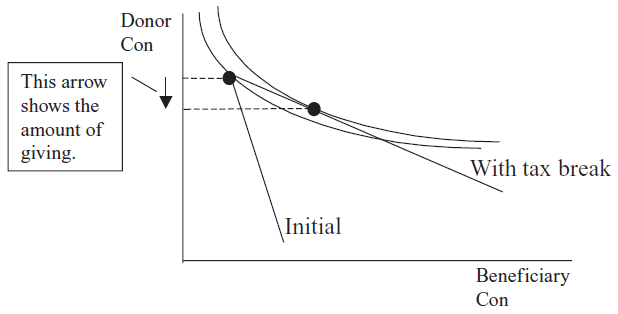 Figure 5.15: The effect of a tax break on giving.
Figure 5.15: The effect of a tax break on giving.But exactly how much giving does the tax break generate? Let’s find out.
STEP With \(c=0.2\) and \(tax\textunderscore break=30\%\), run Solver.
In this case, the tax break has induced charitable giving. It is hard to see on the graph, but the MRS \(= \frac{p_1}{p_2}\) condition (under the chart) tells you the indifference curve is now tangent to the budget line. Figure 15.5 shows what happened.
With a tax break of 30%, we get $1.67 of giving which is 2.1% of the donor’s income (the American giving rate in 2018).
We can also explore how responsive our donor would be to further shocks in the taxbreak. We will compute the tax break elasticity of giving.
STEP Change the tax_break cell to 40%.
That’s a 10 percentage point change in the tax break and a rather hefty 33% change. The budget line swings out a little bit more, but it is hard to see the change in the chart. We know, however, since MRS does not equal \(\frac{p_1}{p_2}\), that we need to re-optimize.
STEP Run Solver.
Charity increased from $1.67 to $3.33. That is a big responsea doubling or 100% increase in giving was generated from a 33% increase in the tax break. That is a tax break elasticity of giving of 3.
STEP Proceed to the CS1 sheet to see a more detailed comparative statics analysis.
Notice that the shock was 1% point, not 10. Notice also that the elasticity from a tax break of 30% to 31% is about 2.87 (H17), not 3. Even though we do not have a reduced form expression, the fact that the measured elasticity depends on the size of the shock tells us that giving is a non-linear function of the tax break.
But regardless of whether it is 3 or 2.87, that high an elasticity is really good news, right? If giving is super-responsive to a tax break, little tweaks in the tax break will generate big increases in giving.
But we need to be careful in how we interpret our result. We do not know whether these preferences and other exogenous variables are representative of many donors. That is an empirical question that requires real-world data. For example, with \(c = 0.5\), tax break increases are much less effective in stimulating more giving.
STEP Click the  button, change c to 0.5 and the tax break to 30%, and run Solver. Charitable giving is at $17.33.
button, change c to 0.5 and the tax break to 30%, and run Solver. Charitable giving is at $17.33.
This makes sense since giving is much higher than it was when \(c=0.2\) and \(tax\textunderscore break=30\%\). But what is the tax break elasticity of giving?
STEP Change the tax break cell to 40% and run Solver. Charitable giving rises to $18.67.
Ponder the computation for a moment. There are a lot of numbers floating around. How would you compute the tax break elasticity of giving?
It is the percentage change in giving divided by the percentage change in the tax break. The numerator is \(\frac{18.67-17.33}{17.33} \approx 7.7\%\). The denominator is 33% (\(\frac{0.4-0.3}{0.3}\)notice that it doesn’t matter if you use the percents version, \(\frac{40\%-30\%}{30\%}\)). Thus, the tax break elasticity is \(\frac{7.7\%}{33\%} = 0.23\).
This result is much less favorable for a policymaker looking to increase charitable giving by manipulating the tax break. For this donor, giving is insensitive to tax break increases.
The Theory of Consumer Behavior can explain a wide variety of giving outcomes. Unfortunately, theory alone does not tell us about the magnitude of a particular effect in the real world. By changing c, we see that the tax break elasticity of giving is drastically affected, ranging from extremely elastic (3) to quite inelastic (0.23). We must gather data and employ econometric techniques to estimate the responsiveness of giving as the tax break changes in the real world. Theory does, however, give us a framework for analyzing the problem.
The Economic Approach Is Widely Applicable
Charitable giving can be viewed through the lens of an Endowment Model using the Theory of Consumer Behavior. The initial endowment is the consumption of the donor and the beneficiary. The donor can choose to give part, all, or none of her endowment to the beneficiary. The amount she gives is determined by that point that maximizes her satisfaction subject to the budget constraint.
We can stimulate giving by lowering the price of giving. This rotates the budget line and yields a new optimal solution. The amount of the increase in giving is an empirical question that cannot be answered by theory alone.
If we view giving as the solution to an optimization problem, we are doing an economic analysis of giving. “An economic analysis” is a phrase often used to communicate that the behavior under consideration will be cast in the framework of optimization and comparative statics.
Many people think economics is about stocks, business, and money. This content-based definition of economics is too limited. Economics is a method of analysis and it can be applied to such “non-economic” issues as charity and many, many other areas.
Seeing charitable giving through the lens of economics does not mean that this is the only way to study charity. The hope is that it provides insight and furthers understanding of what is surely a multifaceted, complex process.
Exercises
- The total change in charitable giving can be explained via the income and substitution effects for giving. For \(c = 0.5\), compute the income and substitution effects when the tax break changes from 30% to 40%. Describe your procedure.
- Use Word’s Drawing Tools to draw a rough sketch of the income and substitution effects for giving, labeling points A, B, and C and using arrows to show the income, substitution, and total effects. Do not include the indifference curves to reduce clutter.
- Income and substitution effects were originally used to explain Giffen goods. If the tax break increase leads to a decrease in charitable giving, is this Giffen behavior? Why or why not?
References
The epigraph is a hadith, which the website islam.uga.edu/hadith.html explains is "a saying of Muhammad or a report about something he did." It would have been easy to find a quotation on charity from any religion because a primary purpose of religion is to encourage us to treat each other with kindness.
If you are thinking of giving to a charitable organization, you can do some background research at www.guidestar.org/ (free registration required to access basic reports) and www.givewell.org/.
Kiva.org is a microcredit organization that allows you to make loans to low-income entrepreneurs all around the world.
If you liked the food stamps application and understand the concept that cash is as good as or better than in-kind (the Carte Blanche Principle), check out www.givedirectly.org.


