The budget constraint
In the preceding section, we assumed that utility is measurable in order to better understand how consumers allocate their budgets, and how this process is reflected in the market demands that are observed. The belief that utility might be measurable is not too extreme in the modern era. Neuroscientists are mapping more and more of the human brain and understanding how it responds to positive and negative stimuli. At the same time, numerous sociological surveys throughout the world ask individuals to rank their happiness on a scale of one to ten, or something similar, with a view to making comparisons between individual-level and group-level happiness – see Application Box 6.2. Nonetheless, not every scientist may be convinced that we should formulate behavioural rules on this basis. Accordingly we now examine the economics of consumer behaviour without this strong assumption. We assume instead that individuals are able to identify (a) different combinations of goods and services that yield equal satisfaction, and (b) combinations of goods and services that yield more satisfaction than other combinations. In contrast to measurable (or cardinal) utility, this concept is called ordinal utility, because it assumes only that consumers can order utility bundles rather than quantify the utility.
Ordinal utility assumes that individuals can rank commodity bundles in accordance with the level of satisfaction associated with each bundle.
The budget constraint
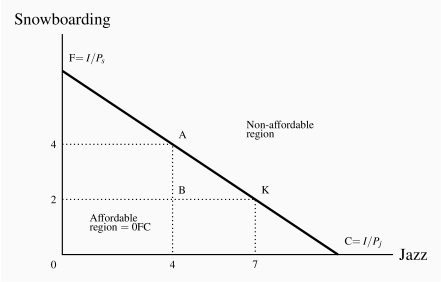
Neal's monthly expenditure limit, or budget constraint, is $200. In addition, he faces a price of $30 for lift tickets and $20 per visit to jazz clubs. Therefore, using S to denote the number of snowboard outings and J the number of jazz club visits, if he spends his entire budget it must be true that the sum of expenditures on each activity exhausts his budget or income (I):
Since many different combinations of the two goods are affordable, it follows that the budget constraint defines all bundles of goods that the consumer can afford with a given budget.
The budget constraint defines all bundles of goods that the consumer can afford with a given budget.
The budget constraint, then, is just what it claims to be—a limit on behaviour. Neal's budget constraint is illustrated in Figure 6.6, where the amount of each good consumed is given on the axes. If he spends all of his $200 income on jazz, he can make exactly ten jazz club visits 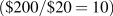 . The calculation also applies to visits to Whistler. The intercept value is always obtained by dividing income by the price of the good or activity in question.
. The calculation also applies to visits to Whistler. The intercept value is always obtained by dividing income by the price of the good or activity in question.
In addition to these affordable extremes, Neal can also afford many other bundles, e.g., (S=2,J=7), or (S=4,J=4), or (S=6,J=1). The set of feasible, or affordable, combinations is bounded by the budget line, and this is illustrated in Figure 6.6.
The affordable set of goods and services for the consumer is bounded by the budget line from above; the non-affordable set lies strictly above the budget line.
The slope of the budget line is informative. As illustrated in Chapter 1, it indicates how many snowboard visits must be sacrificed for one additional jazz visit; it defines the consumer's trade-offs. To illustrate: Suppose Neal is initially at point A (J=4,S=4), and moves to point K (J=7,S=2). Clearly, both points are affordable. In making the move, he trades two snowboard outings in order to get three additional jazz club visits, a trade-off of 2/3. This trade-off is the slope of the budget line, which, in Figure 6.6, is AB/BK=–2/3, where the negative sign reflects the downward slope.
Could it be that this ratio reflects the two prices ($20/$30)? The answer is yes: The slope of the budget line is given by the vertical distance divided by the horizontal distance, OF/OC. The points F and C were obtained by dividing income by the respective price—remember that the jazz intercept is 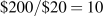 . Formally, that is I/PJ. The intercept on the snowboard axis is likewise I/PS. Accordingly, the slope of the budget constraint is:
. Formally, that is I/PJ. The intercept on the snowboard axis is likewise I/PS. Accordingly, the slope of the budget constraint is:
Since the budget line has a negative slope, it is technically correct to define it with a negative sign. But, as with elasticities, the sign is frequently omitted.
Tastes and indifference
We now consider how to represent a consumer's tastes in two dimensions, given that he can order, or rank, different consumption bundles, and that he can define a series of different bundles that all yield the same satisfaction. We limit ourselves initially to considering just "goods," and not "bads" such as pollution.
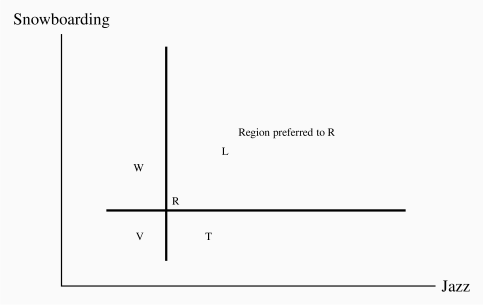
Figure 6.7 examines the implications of these assumptions about tastes. Each point shows a consumption bundle of snowboarding and jazz. Let us begin at bundle R. Since more of a good is preferred to less, any point such as L, which lies to the northeast of R, is preferred to R, since L offers more of both goods than R. Conversely, points to the southwest of R offer less of each good than R, and therefore R is preferred to a point such as V.
Without knowing the consumer's tastes, we cannot be sure at this stage how points in the northwest and southeast regions compare with R. At W or T, the consumer has more of one good and less of the other than at R. Someone who really likes snowboarding might prefer W to R, but a jazz buff might prefer T to R.
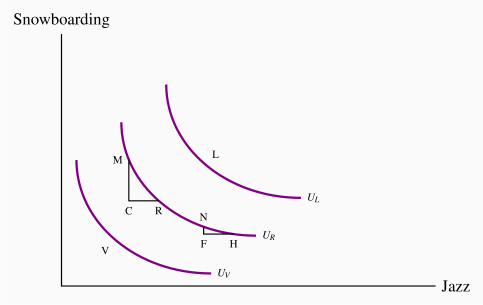
Let us now ask Neal to disclose his tastes, by asking him to define several combinations of snowboarding and jazz that yield him exactly the same degree of satisfaction as the combination at R. Suppose further, for reasons we shall understand shortly, that his answers define a series of points that lie on the beautifully smooth contour UR in Figure 6.8. Since he is indifferent between all points on UR by construction, this contour is an indifference curve.
An indifference curve defines combinations of goods and services that yield the same level of satisfaction to the consumer.
Pursuing this experiment, we could take other points in Figure 6.8, such as L and V, and ask the consumer to define bundles that would yield the same level of satisfaction, or indifference. These combinations would yield additional contours, such as UL and UV in Figure 6.8. This process yields a series of indifference curves that together form an indifference map.
An indifference map is a set of indifference curves, where curves further from the origin denote a higher level of satisfaction.
Let us now explore the properties of this map, and thereby understand why the contours have their smooth convex shape. They have four properties. The first three follow from our preceding discussion, and the fourth requires investigation.
- Indifference curves further from the origin reflect higher levels of satisfaction.
- Indifference curves are negatively sloped. This reflects the fact that if a consumer gets more of one good she should have less of the other in order to remain indifferent between the two combinations.
- Indifference curves cannot intersect. If two curves were to intersect at a given point, then we would have two different levels of satisfaction being associated with the same commodity bundle—an impossibility.
- Indifference curves are convex when viewed from the origin, reflecting a diminishing marginal rate of substitution.
The convex shape reflects an important characteristic of preferences: When consumers have a lot of some good, they value a marginal unit of it less than when they have a small amount of that good. More formally, they have a higher marginal valuation at low consumption levels—that first cup of coffee in the morning provides greater satisfaction than the second or third cup.
Consider the various points on UR, starting at M in Figure 6.8. At M Neal snowboards a lot; at N he boards much less. The convex shape of his indifference map shows that he values a marginal snowboard trip more at N than at M. To see this, consider what happens as he moves along his indifference curve, starting at M. We have chosen the coordinates on UR so that, in moving from M to R, and again from N to H, the additional amount of jazz is the same: CR=FH. From M, if Neal moves to R, he consumes an additional amount of jazz, CR. By definition of the indifference curve, he is willing to give up MC snowboard outings. The ratio MC/CR defines his willingness to substitute one good for the other. This ratio, being a vertical distance divided by a horizontal distance, is the slope of the indifference curve and is called the marginal rate of substitution, MRS.
The marginal rate of substitution is the slope of the indifference curve. It defines the amount of one good the consumer is willing to sacrifice in order to obtain a given increment of the other, while maintaining utility unchanged.
At N, the consumer is willing to sacrifice the amount NF of boarding to get the same additional amount of jazz. Note that, when he boards less, as at N, he is willing to give up less boarding than when he has a lot of it, as at M, in order to get the same additional amount of jazz. His willingness to substitute diminishes as he moves from M to N: The quantity NF is less than the quantity MC. In order to reflect this taste characteristic, the indifference curve has a diminishing marginal rate of substitution: A flatter slope as we move down along its surface.
A diminishing marginal rate of substitution reflects a higher marginal value being associated with smaller quantities of any good consumed.
Optimization
We are now in a position to examine how the consumer optimizes—how he gets to the highest level of satisfaction possible. The constraint on his behaviour is the affordable set defined in Figure 6.6, the budget line.
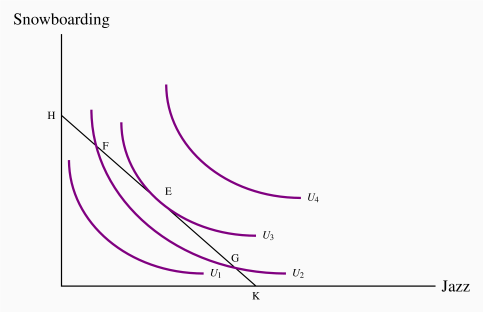
Figure 6.9 displays several of Neal's indifference curves in conjunction with his budget constraint. We propose that he maximizes his utility, or satisfaction, at the point E, on the indifference curve denoted by U3. While points such as F and G are also on the boundary of the affordable set, they do not yield as much satisfaction as E, because E lies on a higher indifference curve. The highest possible level of satisfaction is attained, therefore, when the budget line touches an indifference curve at just a single point—that is, where the constraint is tangent to the indifference curve. E is such a point.
This tangency between the budget constraint and an indifference curve requires that the slopes of each be the same at the point of tangency. We have already established that the slope of the budget constraint is the negative of the price ratio (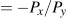 ). The slope of the indifference curve is the marginal rate of substitution MRS. It follows, therefore, that the consumer optimizes where the marginal rate of substitution equals the slope of the price line.
). The slope of the indifference curve is the marginal rate of substitution MRS. It follows, therefore, that the consumer optimizes where the marginal rate of substitution equals the slope of the price line.
Optimization requires:
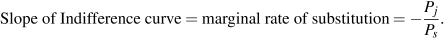 |
(6.3) |
A consumer optimum occurs where the chosen consumption bundle is a point such that the price ratio equals the marginal rate of substitution.
Notice the resemblance between this condition and the one derived in the first section as Equation 6.2. There we argued that equilibrium requires the ratio of the marginal utilities be same as the ratio of prices. Here we show that the MRS must equal the ratio of prices. In fact, with a little mathematics it can be shown that the MRS is indeed the same as the (negative of the) ratio of the marginal utilities: 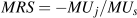 . Therefore the two conditions are in essence the same! However, it was not necessary to assume that an individual can actually measure his utility in obtaining the result that the MRS should equal the price ratio in equilibrium. The concept of ordinal utility is sufficient.
. Therefore the two conditions are in essence the same! However, it was not necessary to assume that an individual can actually measure his utility in obtaining the result that the MRS should equal the price ratio in equilibrium. The concept of ordinal utility is sufficient.
Adjusting to income changes
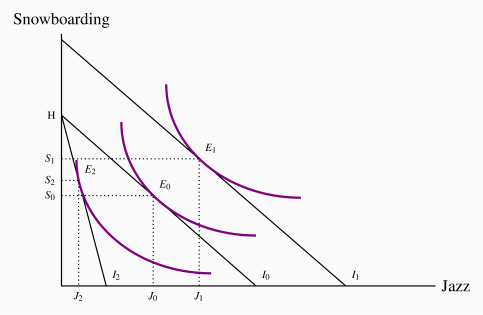
Suppose now that Neal's income changes from $200 to $300. How will this affect his consumption decisions? In Figure 6.10, this change is reflected in a parallel outward shift of the budget constraint. Since no price change occurs, the slope remains constant. By recomputing the ratio of income to price for each activity, we find that the new snowboard and jazz intercepts are 10 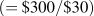 and 15
and 15 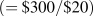 , respectively. Clearly, the consumer can attain a higher level of satisfaction—at a new tangency to a higher indifference curve—as a result of the size of the affordable set being expanded. In Figure 6.10, the new equilibrium is at E1.
, respectively. Clearly, the consumer can attain a higher level of satisfaction—at a new tangency to a higher indifference curve—as a result of the size of the affordable set being expanded. In Figure 6.10, the new equilibrium is at E1.
Adjusting to price changes
Next, consider the impact of a price change from the initial equilibrium E0 in Figure 6.10. Suppose that jazz now costs more. This reduces the purchasing power of the given budget of $200. The new jazz intercept is therefore reduced. The budget constraint becomes steeper and rotates around the snowboard intercept H, which is unchanged because its price is constant. The new equilibrium is at E2, which reflects a lower level of satisfaction because the affordable set has been reduced by the price increase. As explained in Section 6.2, E0 and E2 define points on the demand curve for jazz (J0 and J2): They reflect the consumer response to a change in the price of jazz with all other things held constant. In contrast, the price increase for jazz shifts the demand curve for snowboarding: As far as the demand curve for snowboarding is concerned, a change in the price of jazz is one of those things other than own-price that determine its position.
Philanthropy
Individuals in the foregoing analysis aim to maximize their utility, given that they have a fixed budget. Note that this behavioural assumption does not rule out the possibility that these same individuals may be philanthropic – that is, they get utility from the act of giving to their favourite charity or the United Way or Centre-aide. To see this suppose that donations give utility to the individual in question – she gets a 'warm glow' feeling as a result of giving, which is to say she gets utility from the activity. There is no reason why we cannot put charitable donations on one axis and some other good or combination of goods on the remaining axis. At equilibrium, the marginal utility per dollar of contributions to charity should equal the marginal utility per dollar of expenditure on other goods; or, stated in terms of ordinal utility, the marginal rate of substitution between philanthropy and any other good should equal the ratio of their prices. Evidently the price of a dollar of charitable donations is one dollar.