Price impacts: Complements and substitutes
The nature of complements and substitutes, defined in Chapter 4, can be further understood with the help of Figure 6.10. The new equilibrium E2 has been drawn so that the increase in the price of jazz results in more snowboarding—the quantity of S increases to S2 from S0. These goods are substitutes in this picture, because snowboarding increases in response to an increase in the price of jazz. If the new equilibrium E2 were at a point yielding a lower level of S than S0, we would conclude that they were complements.
Cross-price elasticities
Continuing with the same price increase in jazz, we could compute the percentage change in the quantity of snowboarding demanded as a result of the percentage change in the jazz price. In this example, the result would be a positive elasticity value, because the quantity change in snowboarding and the price change in jazz are both in the same direction, each being positive.
Policy: Income transfers and price subsidies
Government policies that improve the purchasing power of low-income households come in two main forms: Pure income transfers and price subsidies. Social Assistance payments ("welfare") or Employment Insurance benefits, for example, provide an increase in income to the needy. Subsidies, on the other hand, enable individuals to purchase particular goods or services at a lower price—for example, rent or daycare subsidies.
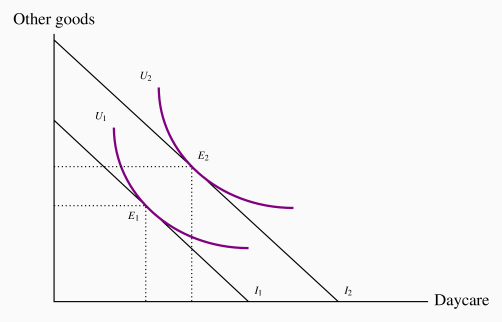
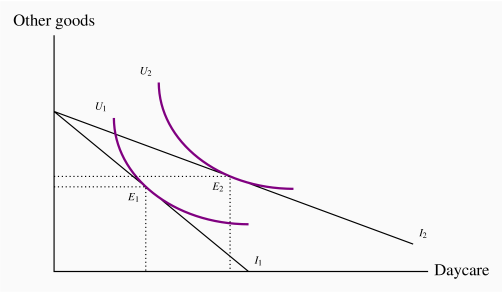
In contrast to taxes, which reduce the purchasing power of the consumer, subsidies and income transfers increase purchasing power. The impact of an income transfer, compared with a pure price subsidy, can be analyzed using Figures 6.11 and 6.12.
In Figure 6.11, an income transfer increases income from I1 to I2. The new equilibrium at E2 reflects an increase in utility, and an increase in the consumption of both daycare and other goods.
Suppose now that a government program administrator decides that, while helping this individual to purchase more daycare accords with the intent of the transfer, she does not intend that government money should be used to purchase other goods. She therefore decides that a daycare subsidy program might better meet this objective than a pure income transfer.
A daycare subsidy reduces the price of daycare and therefore rotates the budget constraint outwards around the intercept on the vertical axis. At the equilibrium in Figure 6.12, purchases of other goods change very little, and therefore most of the additional purchasing power is allocated to daycare.
Let us take the example one stage further. From the initial equilibrium 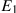 in Figure 6.12, suppose that, instead of a subsidy that took the individual to
in Figure 6.12, suppose that, instead of a subsidy that took the individual to 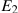 , we gave an income transfer that enabled the consumer to purchase the combination
, we gave an income transfer that enabled the consumer to purchase the combination 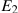 . Such a transfer is represented in Figure 6.13 by a parallel outward shift of the budget constraint from
. Such a transfer is represented in Figure 6.13 by a parallel outward shift of the budget constraint from 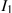 to
to 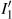 , going through the point
, going through the point 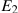 . We now have a subsidy policy and an alternative income transfer policy, each permitting the same consumption bundle (
. We now have a subsidy policy and an alternative income transfer policy, each permitting the same consumption bundle (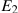 ). The interesting aspect of this pair of possibilities is that the income transfer will enable the consumer to attain a higher level of satisfaction—for example, at point
). The interesting aspect of this pair of possibilities is that the income transfer will enable the consumer to attain a higher level of satisfaction—for example, at point 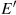 —and will also induce her to consume more of the good on the vertical axis. The higher level of satisfaction comes about because the consumer has more latitude in allocating the additional real income.
—and will also induce her to consume more of the good on the vertical axis. The higher level of satisfaction comes about because the consumer has more latitude in allocating the additional real income.
Application Box 6.3 Daycare subsidies in Quebec
The Quebec provincial government subsidizes daycare heavily. In the public-sector network called the "Centres de la petite enfance", families can place their children in daycare for less than $10 per day, while families that use the private sector are permitted a generous tax allowance for their daycare costs. This policy is designed to enable households to limit the share of their income expended on daycare. It is described in Figure 6.13.
The consequences of strong subsidization are not negligible: Excess demand, to such an extent that children are frequently placed on waiting lists for daycare places long before their parents intend to use the service. Annual subsidy costs amount to almost $2 billion per year. At the same time, it has been estimated that the policy has enabled many more parents to enter the workforce than otherwise would have.
The price of giving
Imagine now that the good on the horizontal axis is charitable donations, rather than daycare, and the government decides that for every dollar given the individual will see a reduction in their income tax of 50 cents. This is equivalent to cutting the 'price' of donations in half, because a donation of one dollar now costs the individual half of that amount. Graphically the budget constraint rotates outward with the vertical intercept unchanged. Since donations now cost less the individual has increased spending power as a result of the price reduction for donations. The price reduction is designed to increase the attractiveness of donations to the utility maximizing consumer.
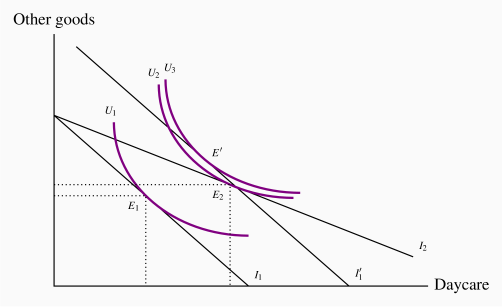
 ; but it also permits him to attain a higher level of satisfaction, denoted by
; but it also permits him to attain a higher level of satisfaction, denoted by 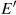 on the indifference curve U3.
on the indifference curve U3.

