15: Theories of Financial Markets
- Last updated
- Save as PDF
- Page ID
- 46263
Goals and Objectives:
In this chapter, we will do the following:
- Explain how the rate of interest is defined and measured
- Explore the relationship between the bond market and the loanable funds market
- Analyze a neoclassical general equilibrium model of interest rate determination
- Incorporate the stock market into the neoclassical theory of interest rate determination
- Investigate an Austrian theory of interest rate determination
- Examine a Marxian theory of interest rate determination
Prior to this chapter, our exploration of macroeconomic theory has been focused on theories of the business cycle. That is, we have concentrated mostly on factors that influence the overall amount of economic activity, the total production of commodities, and the amount of unemployment. In this chapter, we turn to theories of financial markets. The financial markets have an important role to play in market capitalist economies and if we are to gain a deeper understanding of macroeconomic policy in later chapters, we must first learn to think about how the financial markets work and how they interact with the rest of the economy. Once we have developed a more complete understanding of interest rates, bonds, and stocks, we will then be able to explore in detail the neoclassical, Austrian, and Marxian theories of interest rate determination.
The Definition and Measurement of the Rate of Interest
The rate of interest, or the interest rate, is simply an amount of money paid to a lender by a borrower for the use of money during a specific period, expressed as a percentage of the amount borrowed. For example, if a lender receives $5 in payment for the use of a $100 loan during a year, then the annual interest rate is 5% (= $5/$100). In this case, the $100 is referred to as the principal amount of the loan, and the $5 is the dollar amount of the interest. If the principal is returned at the end of one year, then that will be the end of the transaction. The lender will have received $105. This growth of the principal is captured in the simple diagram in Figure 15.1.

On the other hand, if the loan is renewed, then a situation of compound interest arises. That is, the lender leaves the $105 with the borrower at the end of the year, and then the lender expects to receive a 5% interest payment at the end of the second year calculated using the entire $105 loaned at the beginning of the second year. The calculation of the future value (FV) of the original loan amount of $100 at time t = 2 is as follows:
The growth of the principal using compound interest in this scenario is captured with the diagram in Figure 15.2.
 If the period of the loan is three years, then the future value will be even larger, again as a result of compound interest. The calculation of the future value in time t = 3 is as follows:
If the period of the loan is three years, then the future value will be even larger, again as a result of compound interest. The calculation of the future value in time t = 3 is as follows:
The growth of the principal using compound interest in this scenario is captured with the diagram in Figure 15.3.
 In general, if the annual interest rate is i, the present value amount (or the initial loan amount) is PV, and the loan is made for n years, then the calculation of the future value is as follows:
In general, if the annual interest rate is i, the present value amount (or the initial loan amount) is PV, and the loan is made for n years, then the calculation of the future value is as follows:
In the examples we just considered, a sum of money was loaned out and we explored how much it would be worth at the end of the loan period. That is, we considered the sum’s future value. It is often the case, however, that we are confronted with different information. For example, we might know the future payment that is to be received in a known number of years. If we also know the interest rate, then we can calculate the present value of that sum by simply rearranging the future value formula as follows:
To use our earlier example, suppose that a lender knows she will receive $115.76 at the end of three years. If she knows that the annual interest rate is 5%, then she can arrive at the present value in the following way:
In other words, it is possible to equate future dollars with present dollars using the interest rate. The idea is rather intuitive. It means that future dollars are worth less than present dollars to a person. Wouldn’t you rather have $100 today than in three years? Of course, you would. How large would the future sum need to be before you would consider it equivalent to the $100 today? According to the information reflected in the current rate of interest, the answer is $115.76.
When this method of determining the present value of a future sum is used, it is said that the future sum has been discounted to the present using the interest rate. The present value formula and the method of discounting are especially useful when we wish to know the present value of a specific financial asset. For example, a creditor (or lender) might purchase an asset, such as a bond. A bond is really just a financial contract between a lender and a borrower, much like an IOU. When a creditor purchases a newly issued bond, she hands over a sum of money to a borrower. The borrower agrees to repay the amount borrowed when the bond matures. In the case of coupon bonds, the borrower also agrees to make periodic payments of interest to the lender until the bond matures. If we know what the future payments will be, then we can discount each payment back to the present and then simply sum them up to determine the present value of the bond.
For example, suppose that a bond pays $100 in interest annually for the next five years. This situation is depicted in the diagram in Figure 15.4.
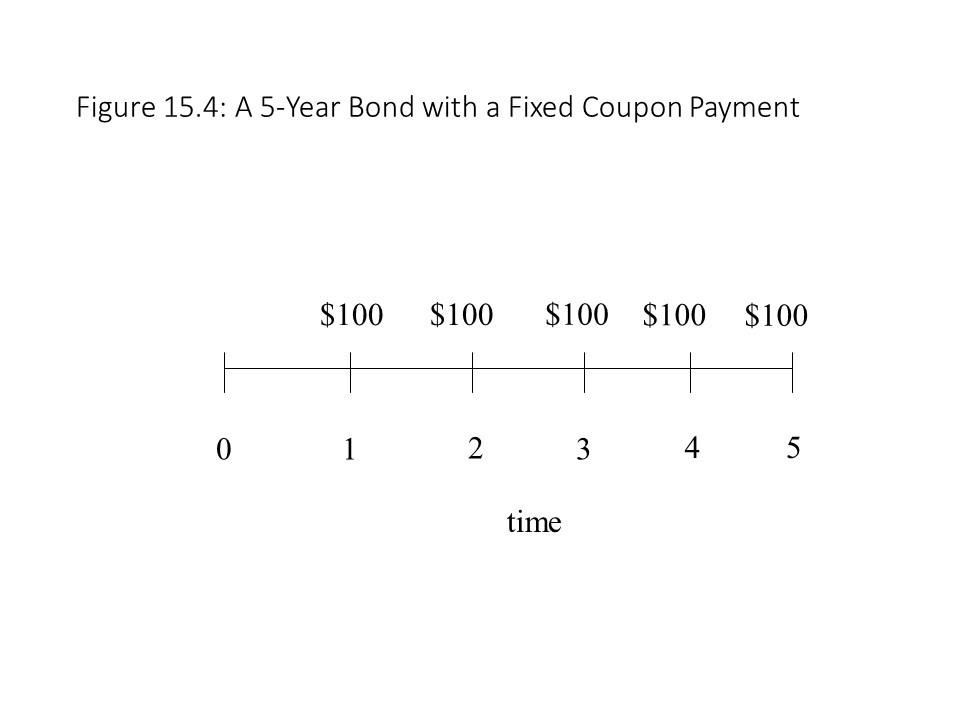 If we know that the interest rate is 5% and we ignore the repayment of principal for simplicity, then we can calculate the present value of the bond as follows:
If we know that the interest rate is 5% and we ignore the repayment of principal for simplicity, then we can calculate the present value of the bond as follows:
For this calculation, the reader should notice that each future payment of $100 is being discounted back to the present before being summed up. Furthermore, each future payment is being discounted according to how many years will pass before it is received. That is, the final payment in year 5 is discounted the most (5 times). The payment at the end of year 1 is discounted the least (once). Finally, the reader should notice that the straightforward sum of the future payments is $500, but the present value is only $432.95. The reason, of course, is that the future payments are not worth $500 today due to the existence of discounting.
The important point to notice is that we can determine the present value of a bond or any financial asset if we know the future payments associated with the asset, the rate of interest, and the term to maturity (i.e., the number of years to maturity). Imagine that an investor is considering the purchase of several different assets, each with a different number of years to maturity and a different periodic payment. The only rational way to compare these different assets is to use the current interest rate to discount the future payments associated with each asset back to the present. Once the values of the different assets are determined for the present period, their values can be easily compared.
In these examples, we have been assuming that the interest rate is a known quantity. It is possible that an investor might be considering the purchase of a bond, but he only knows the amount of the periodic interest payments, the term to maturity, and the price of the bond. For example, suppose that the periodic payment is $100, the term is 5 years, and the price of the bond is $400. The investor would like to know the interest rate associated with the bond, which is also referred to as the yield to maturity (YTM). To calculate the yield, it is only necessary to determine the interest rate that will equate the current price of the bond with the present value of its future payments as follows:
This calculation is difficult without a financial calculator. It can be obtained through a trial and error method. The solution is approximately a 7.93% rate of interest. Using this method, it is possible to measure the rate of interest that applies to a specific financial asset.
The reader should also notice that because the price of the bond is below $432.95, the yield on the bond is above 5%. That is, when an investor pays a lower price for the bond, with the periodic interest payments fixed, the yield is necessarily higher. This result is consistent with the widely reported relationship between interest rates and bond prices that one hears in the financial news: Interest rates and bond prices are always inversely related.
Economists of all persuasions tend to refer to the rate of interest as though it is a single entity. In reality, many different interest rates exist in market capitalist economies. Each corresponds to a different loan or asset. Interest rates exist for 12-month certificates of deposit, online savings accounts, 15-year mortgage loans, 30-year mortgage loans, 10-year Treasury bonds, 2-year auto loans, and so on. The reason that economists often refer to a single interest rate is that the many different interest rates that exist tend to move together. Economists do have theories as to how and why interest rates differ from one another, but frequently they are interested in explaining the overall movement of interest rates instead. In the latter case, they refer simply to “the interest rate.”[1]
We are now in possession of a clear definition and method of measurement of the rate of interest. We have also learned how to calculate the future value of a present sum and the present value of a future sum. These tools will be very useful as we consider linkages between different financial markets in the next several sections of this chapter.
The Relationship b etween the Bond Market and the Loanable Funds Market
We are now in a position to identify the linkage between two key financial markets that exist in capitalist economies: the bond market and the loanable funds market. Although we discuss these markets as though they are two separate markets, each can be thought of as the mirror reflection of the other and so they are really one and the same.
The loanable funds market is the market for financial loans. Like any market, it has both a supply side and a demand side. On the supply side of the market are the lenders who possess loanable funds that they wish to lend to borrowers for a period of time in exchange for interest. The supply curve of loanable funds is upward sloping as shown in Figure 15.5 (a). That is, as the rate of interest increases, the quantity of loanable funds that lenders are willing and able to provide increases. The rate of interest may be thought of as the price paid for the use of these funds, and so the supply curve is upward sloping, as it is in most product markets. The demand curve for loanable funds is downward sloping, which is also shown in Figure 15.5 (a). It slopes downward because as the interest rate falls, more investment projects become profitable for businesses, and so businesses are willing and able to borrow more loanable funds.
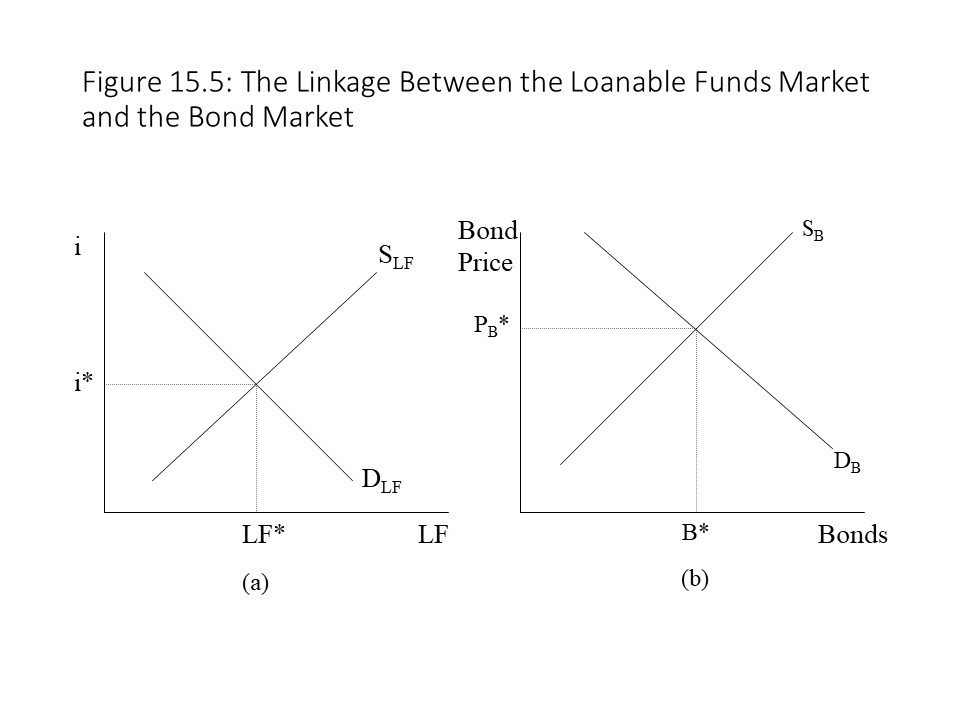 It should be clear that an equilibrium interest rate exists in this market. That is, the interest rate that occurs at the intersection of the two curves represents the interest rate that clears the market for loanable funds of both surpluses and shortages. If the interest rate is above the equilibrium interest rate, i*, then an excess supply or a surplus of loanable funds exists. In that case, more suppliers wish to lend than borrowers wish to borrow due to the high interest rate. As a result, competition among lenders will drive the interest rate down towards the equilibrium level. Alternatively, if the interest rate is below the equilibrium interest rate, i*, then an excess demand or a shortage of loanable funds exists. In that case, more borrowers wish to borrow than lenders wish to lend at the low interest rate. As a result, competition for the limited funds available will drive the interest rate up towards the equilibrium level. It should also be noted that an equilibrium quantity of loanable funds, LF*, is determined as well when the market is in equilibrium.
It should be clear that an equilibrium interest rate exists in this market. That is, the interest rate that occurs at the intersection of the two curves represents the interest rate that clears the market for loanable funds of both surpluses and shortages. If the interest rate is above the equilibrium interest rate, i*, then an excess supply or a surplus of loanable funds exists. In that case, more suppliers wish to lend than borrowers wish to borrow due to the high interest rate. As a result, competition among lenders will drive the interest rate down towards the equilibrium level. Alternatively, if the interest rate is below the equilibrium interest rate, i*, then an excess demand or a shortage of loanable funds exists. In that case, more borrowers wish to borrow than lenders wish to lend at the low interest rate. As a result, competition for the limited funds available will drive the interest rate up towards the equilibrium level. It should also be noted that an equilibrium quantity of loanable funds, LF*, is determined as well when the market is in equilibrium.It is interesting to note that the suppliers in the one market are the demanders in the other market. Similarly, the demanders in the one market are the suppliers in the other market. For example, if I wish to borrow funds in the loanable funds market, then I am on the demand side of that market. At the same time, I can only obtain loanable funds by selling bonds in this scenario, and so I am on the supply side in the bond market. Similarly, if I wish to lend funds in the loanable funds market, then I am on the supply side of that market. At the same time, I can only lend loanable funds by buying bonds in this scenario, and so I am on the demand side in the bond market. To summarize:
- Demanders of loanable funds = Suppliers of bonds ⇒ Borrowers
- Suppliers of loanable funds = Demanders of bonds ⇒ Lenders
Because of this logical connection between the two markets, we regard the loanable funds market as the mirror reflection of the bond market. It follows that if one of the markets is in equilibrium, the other market must also be in equilibrium. A natural question to ask then is whether a definite relationship exists between the equilibrium bond price and the equilibrium interest rate.
The answer to this question is that the equilibrium bond price will equal the present value of the bond calculated using the equilibrium interest rate. For example, suppose that we know the term to maturity for a bond to be 5 years, the initial loan amount to be A, and the equilibrium interest rate to be i*. Using this information, it is possible to calculate the present value of the bond when the loanable funds market is in equilibrium. It is this present value calculation that also yields the equilibrium price of the bond, PB*, as shown below:
It might not be obvious why the price of the bond has an inherent tendency to move towards this level, PB*. The argument must be made, however, if the claim is to be defended that this bond price is an equilibrium one. To understand why this bond price represents the equilibrium bond price, consider what will happen if the price of the bond is different from this level. For example, suppose the price of the bond is above the present value as calculated here. In that case, investors will not want to purchase the bond. Who would pay more for a bond than its present value? The demand for the bond will fall, which places downward pressure on the bond price. Similarly, bondholders will be eager to sell the bond. Who will want to hold a bond when it can be sold at a price that exceeds its present value? The increase in supply will also put downward pressure on the bond price. Hence, both factors push the price of the bond down towards the present value of the bond and towards PB*. To summarize:
If PB* > PV then demand falls and supply rises until PB*=PV.Alternatively, consider what will happen if the price of the bond is below the present value as calculated here. In that case, investors will want to purchase the bond. Who would not want to purchase a bond when its price is less than its present value? It’s a bargain. The demand for the bond will rise, putting upward pressure on the price of the bond. Similarly, bondholders will not want to sell the bond. Who would sell a bond when its price is below what it is worth in today’s terms? The reduction in supply will put upward pressure on the bond price. Hence, both factors push the price of the bond up towards the present value of the bond and towards PB*. To summarize:
If PB* < PV then demand rises and supply falls until PB*=PV.Overall, we see that the equilibrium interest rate and the equilibrium bond price are related in a precise manner as reflected in the present value formula.
Finally, it is helpful to consider what will happen when equilibrium is disrupted in these markets. Suppose that the demand for loanable funds rises as a result of businesses becoming more optimistic about the health of the economy. A rightward shift of the demand curve for loanable funds will cause a rise in the equilibrium interest rate as shown in Figure 15.6 (a).
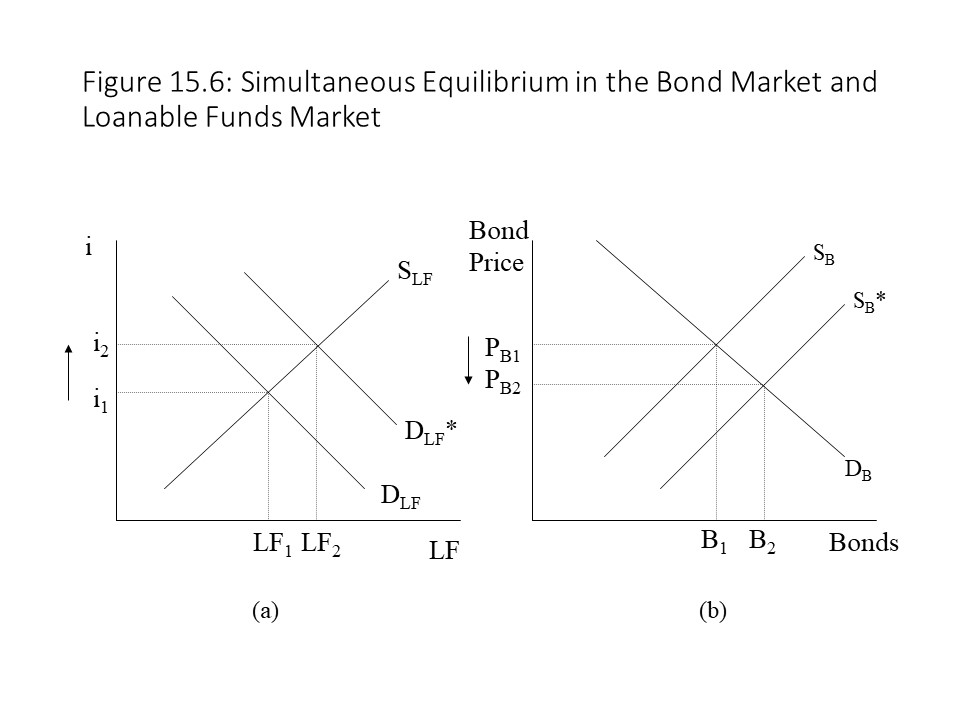 At the same time, because the demanders of loanable funds are also the suppliers of bonds, the supply curve of bonds will shift to the right in the bond market as shown in Figure 15.6 (b). The result will be a reduction in the equilibrium bond price. It is worth noting that this result of an inverse relationship between the interest rate and the bond price is consistent with the same conclusion drawn earlier from the present value formula.
At the same time, because the demanders of loanable funds are also the suppliers of bonds, the supply curve of bonds will shift to the right in the bond market as shown in Figure 15.6 (b). The result will be a reduction in the equilibrium bond price. It is worth noting that this result of an inverse relationship between the interest rate and the bond price is consistent with the same conclusion drawn earlier from the present value formula.
The Market for Money
In addition to the bond and loanable funds markets, mainstream economists typically also discuss a third financial market that is referred to as the money market. This concept can easily become the source of great confusion because of the different meanings of this phrase.[2] In the financial services industry, the money market refers to the market for short term securities. That is, assets with terms to maturity of less than one year are referred to as money market instruments. Three-month Treasury bills, six-month certificates of deposit, and commercial paper are all examples of assets that involve repayment of principal and interest to a lender in a period of less than one year. Investors purchase these assets to earn interest income using their short-term savings.
It is crucial to understand that the money market we will be discussing in this section is not the money market to which professionals in the financial services industry refer. Indeed, the money market to which financial services professionals refer is much closer to the bond market that we have been discussing, although many bonds have terms to maturity of much longer than one year. Instead, when mainstream economists refer to the money market, they have in mind a theoretical construct that derives from the work of John Maynard Keynes’s 1936 book The General Theory of Employment, Interest, and Money that we discussed in Chapter 13. Because this “market” is rather unusual, we will need to devote some space to this notion. Once the money market is completely understood, we can complete the picture of the neoclassical theory of interest rate determination.
Consider for a moment, the finances of a single household. The household has accumulated a large collection of assets, which includes a home, two automobiles, a savings account, some stocks, some bonds, a certificate of deposit, a checking account, some currency (paper money and coins), and a boat. At any one point in time, the total value of the household’s assets is divided into these different components, and it is possible to identify the dollar value that corresponds to each component, as shown in Figure 15.7.

Of all these different assets, neoclassical economists only consider the checking account and the currency to constitute money. Money, according to the neoclassical perspective, refers to anything that can be readily used for transactions. Only the most liquid assets qualify. Liquidity refers to the ease of conversion of an asset into currency. Currency is obviously the most liquid asset. Checking accounts are also extremely liquid. The funds are payable on demand and checks and debit cards can be easily used to engage in transactions. Savings deposits and certificates of deposit are less liquid because check writing is not possible and withdrawal restrictions apply to each. Stocks and bonds must be sold, which requires payment of a brokerage fee so they are not as liquid as currency or checkable deposits. The least liquid assets for the household are the home, the automobiles, and the boat. These must be sold, which takes time and is costly. Because currency and checkable deposits are the most liquid assets, neoclassical economists typically only consider them to be money.
Given this definition of money, the household’s actual money holdings consist of the sum of its currency holdings and its checkable deposits. On the other hand, this household’s demand for money refers to its desired money holdings, given its wealth. Of course, it is possible that the household’s desired holdings and its actual holdings do not agree. If the household wishes to hold the same amount of money that it is holding in Figure 15.7, however, then this amount constitutes the household’s demand for money.
It is important not to be confused by the concept of money demand. One might think that the demand for money should always be infinite because everyone always wants more of every good and asset, including money, according to the neoclassical way of thinking. This conclusion would be incorrect, however, because money demand only refers to desired money holdings given the assetsof the household. That is, how much of the household’s assets does it wish to hold in the form of money? It may wish to hold a lot of its assets in the form of money or only a little depending on the benefits it perceives to flow from the holding of money.
What are the benefits that flow from the holding of money? Why would a household hold any money? The classical economists considered this question and provided a helpful, albeit somewhat obvious answer. People hold money for the purpose of engaging in transactions. This transactions demand for money forms one part of the household’s money demand. That is, the household requires money if it is to pay for goods and services. A household cannot survive for very long in a market capitalist society if it refuses to use money. Bills must be paid and groceries must be purchased. Clearly, the transactions demand for money seems to be an important piece of the puzzle.
Why else might a household decide to hold some of its assets in the form of money? Keynes offered an additional reason why a household might choose to hold money. Even if the household is not interested in using the money for planned transactions, it might wish to hold some money strictly for precautionary reasons. That is, the fear of unplanned medical expenses might lead a household to maintain an emergency savings fund, just in case. Fear of an unanticipated job loss might be another reason to hold wealth in the form of money. Neoclassical economists refer to this type of money demand as the precautionary demand for money. This factor might also be contributing to the money demand represented in Figure 15.7.
If we wish to draw the demand curves representing the transactions demand (DT) and the precautionary demand (DP) for money, we can do so as in Figure 15.8.[3]

Figure 15.8 suggests that the sum of these two components of money demand (DT+DP) will be represented as a vertical line when the interest rate is placed on the vertical axis. That is, neither of these components of money demand depends on the interest rate. As the interest rate rises, the quantity of money demanded remains the same because households still wish to engage in the same volume of transactions and maintain the same precautionary balances in case of emergencies. When money income changes, however, the transactions demand and precautionary demand increase, and so these curves shift to the right. That is, households will want to purchase more goods and services, and they will prefer to hold more money in case of emergencies. A reduction in money incomes would lead to leftward shifts for similar reasons.
Finally, Keynes identified a third motive for holding money. He argued that a household might hold money purely for speculative reasons. That is, a household might wish to hold money so it might be used to purchase bonds if interest rates unexpectedly rise to higher-than-normal levels. Due to the inverse relationship between bond prices and interest rates, the drop in bond prices will make them attractive investments. Once interest rates fall and bond prices rise to their original, normal levels, the household will enjoy a capital gain. A capital gain is the difference between the selling price and the purchase price of an asset. This speculative demand for money offers a third way to understand the demand for money represented in Figure 15.7.
Although Keynes wrote about the speculative demand for money, neoclassical economists often think in terms of the asset demand for money, which is like the speculative demand for money.[4] If money is thought about as an asset, then it can be compared to the other assets the household owns. Initially, it might appear that money is a terrible asset. A home is a great long-term investment because home prices frequently increase over time at a rate greater than most prices. As a result, a homeowner might experience a capital gain when she finally sells the house, and in the meantime, the members of the household have been able to enjoy the benefits of living in the home. Stocks and bonds may also be sold to realize capital gains, and they pay dividends and interest, respectively, while they are owned. Even savings accounts and CDs pay interest to their owners. Money, however, generally pays no interest. Currency in your wallet and checkable deposits do not pay interest.
What does money have to recommend it then as an asset? The answer: its liquidity. Assets are not only evaluated on the basis of their expected return. Their degree of liquidity is also an important characteristic that is important to investors. Because money is the most liquid asset available, it is typically held as an asset. Remember, if this component of money demand exists, then a part of the total money held by the household is not for the purpose of making transactions or for precautionary reasons. It is held simply because money is one asset among several that the household considers to be worth holding. The asset demand for money depends on a household’s money (or nominal income), just like the transactions demand and the precautionary demand. As a household’s money income rises, its wealth increases, and it will choose to hold more of all assets, including money.
The asset demand for money also depends, however, on another key factor: the rate of interest. As the rate of interest rises, interest-bearing assets become relatively more desirable. That is, the opportunity cost of holding money as an asset increases. Households, therefore, wish to hold less money, and the quantity of money demanded declines. Alternatively, as the rate of interest declines, the quantity of money demanded increases because the opportunity cost of holding it falls. That is, interest-bearing assets become relatively less attractive, and the liquidity characteristic of money makes it seem like a relatively more attractive asset. If we place the rate of interest on the vertical axis and the quantity of money demanded on the horizontal axis, then the curve representing the asset demand for money (DA) is downward sloping, indicating an inverse relationship between the quantity of money demanded and the interest rate. This situation is depicted in Figure 15.9.
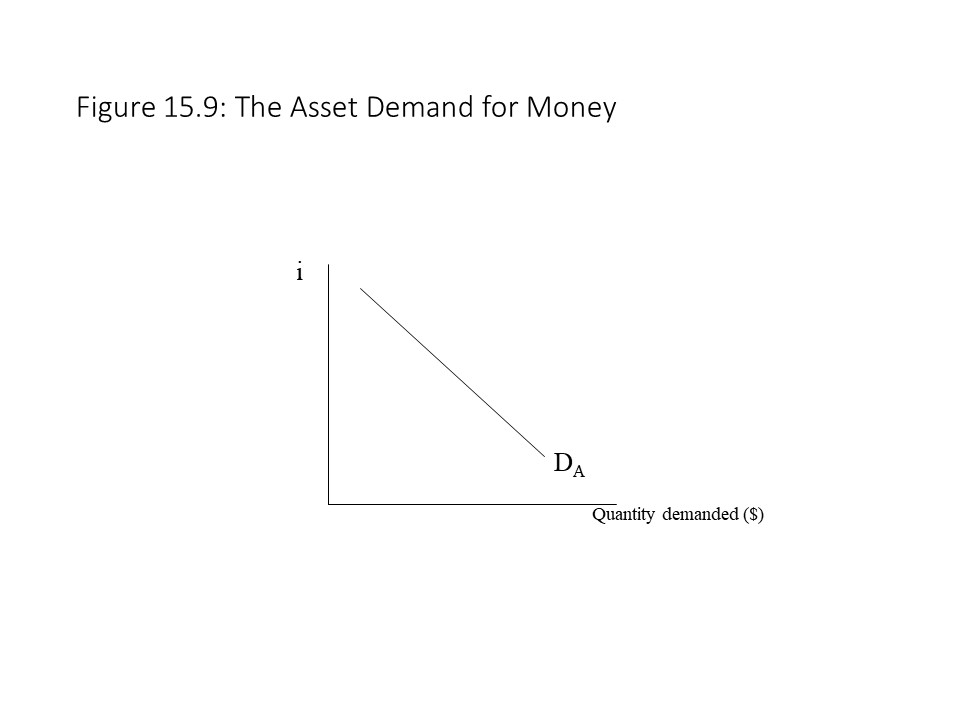 A rise in money income will shift the money demand curve to the right because of the positive affect on wealth and the demand for all assets. Its downward slope, however, is entirely the result of the negative relationship between money demand and the interest rate.
A rise in money income will shift the money demand curve to the right because of the positive affect on wealth and the demand for all assets. Its downward slope, however, is entirely the result of the negative relationship between money demand and the interest rate.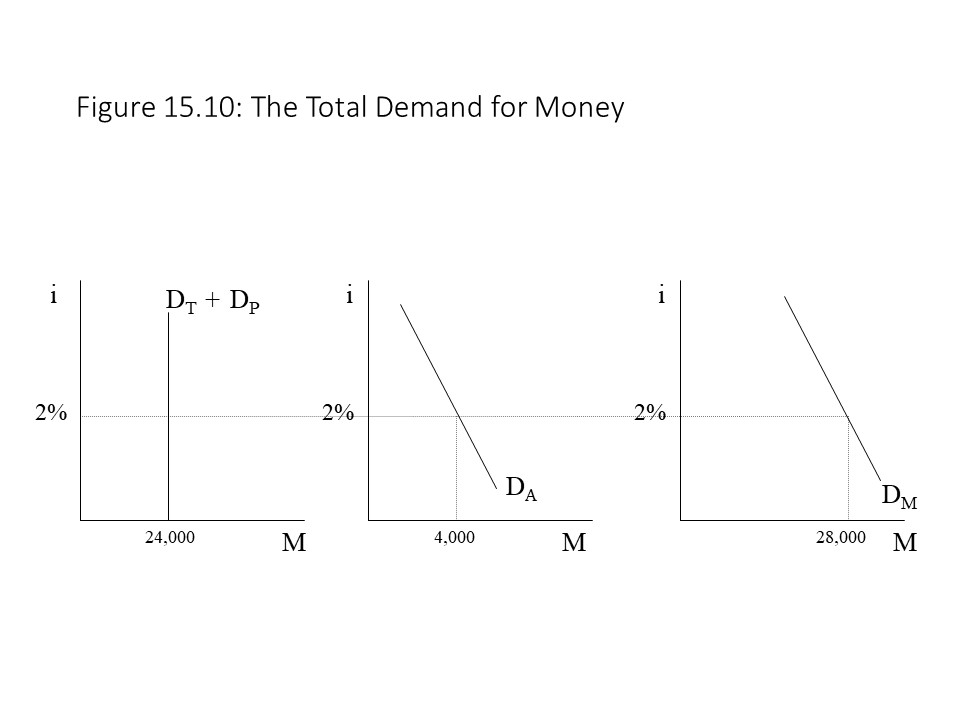 The total money demand curve will be downward sloping as a result of the downward slope of the asset money demand curve. Because it represents the sum of all three curves, it lies further to the right than any one of the curves taken individually. As before, a change in money income will shift the money demand curve in the direction of the change.
The total money demand curve will be downward sloping as a result of the downward slope of the asset money demand curve. Because it represents the sum of all three curves, it lies further to the right than any one of the curves taken individually. As before, a change in money income will shift the money demand curve in the direction of the change.
Up until this point, we have been discussing the demand for money originating with a single household. Of course, each household will have its own money demand curve, reflecting its desire to hold money for transactions, for precautionary reasons, and as an asset. If we aggregate all these individual households’ demands and all the firms’ demands for money (after all, businesses will desire to hold money as well for various reasons), then we obtain the aggregate money demand curve for the entire economy. It should also be downward sloping for the reasons described in this section. Using the aggregate money demand curve, we now have a completely developed notion of one side of the market that neoclassical economists call the money market.
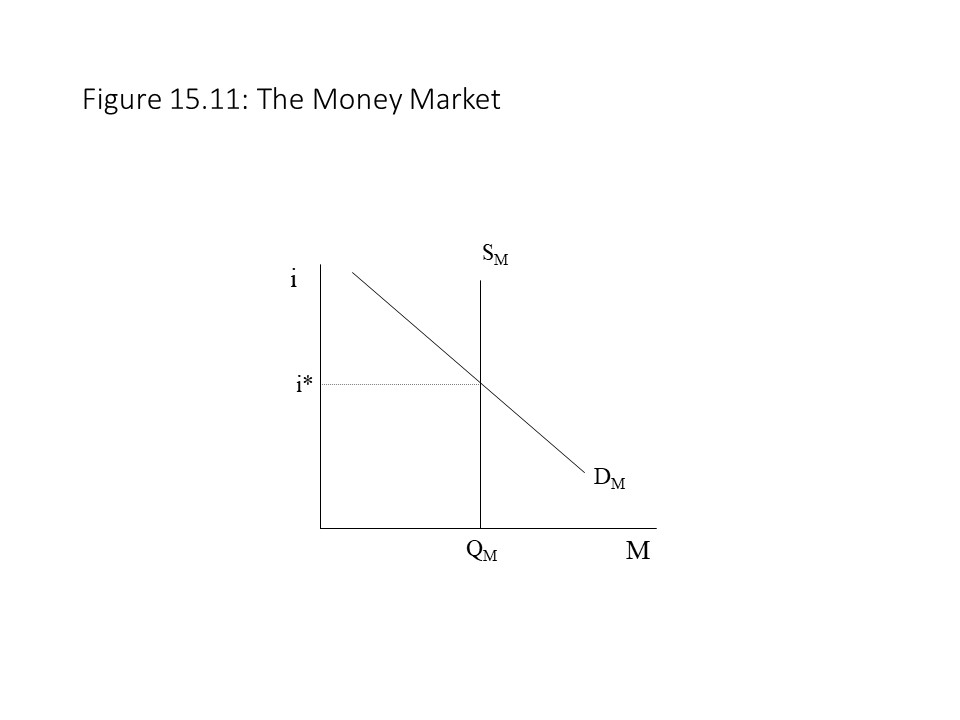
The demand side of the money market refers to desired money holdings. Actual money holdings, however, are reflected in the supply side of the money market. The supply of money is collectively determined by the nation’s central bank, the commercial banks, and the depositors. Among these three, the central bank has the greatest influence over the money supply. In the United States, the Federal Reserve (referred to as “The Fed”) serves as the central bank. It has the power to determine the quantity of checkable deposits and currency in circulation. In other words, the Fed determines the quantity of money supplied. At this stage, we assume that the money supply is exogenously determined. That is, the money supply is determined by central bankers, and it is independent of the interest rate. Therefore, the money supply curve (SM) is perfectly vertical as shown in Figure 15.11.
 If the Fed increases the money supply, then the money supply curve shifts to the right. If the Fed reduces the money supply, then the money supply curve shifts to the left.
If the Fed increases the money supply, then the money supply curve shifts to the right. If the Fed reduces the money supply, then the money supply curve shifts to the left.
It is also worth noting that the supply and demand curves intersect at a specific interest rate (i*) in the money market. At this interest rate, the quantity of money that households and firms actually hold equals the quantity that households and firms desire to hold. That is, actual money holdings equal desired money holdings. In this situation, households and firms have no reason to modify their behavior, and so this interest rate represents the equilibrium rate of interest. What is not clear at this stage is how equilibrium is achieved in this market. We provide the answer to this question in the next section.
A Neoclassical General Equilibrium Model of Interest Rate Determination
In this section, we will consider a neoclassical general equilibrium model of interest rate determination. A general equilibrium model is a model that demonstrates how multiple markets simultaneously arrive at an equilibrium outcome. In earlier chapters, our focus was on partial equilibrium models. A partial equilibrium model demonstrates how a single market reaches an equilibrium outcome. Because partial equilibrium models are very easy to explain, neoclassical economists are fond of using such models at the introductory level. When discussing financial markets, however, it is helpful to use a general equilibrium framework that links together the loanable funds market, the bond market, and the money market. It can be shown that a change in any one market leads to the clearing of the other markets.
The first economist to rigorously develop a mathematical model of general equilibrium was the French economist Leon Walras. In the 1870s, Walras was one of the three economists to independently emphasize marginal changes as central to rational economic decision making. William Stanley Jevons in Britain and Carl Menger in Austria were the other two economists to participate in what would later be dubbed the marginalistrevolution. The new approach to economic analysis was considered significant enough that later economists would regard this change as an event separating old-fashioned classical economics from modern neoclassical economics. Walras’s work was unique, however, in that he also developed a theory of general economic equilibrium.
An important part of Walrasian general equilibrium theory is something called Walras’s Law. Walras’s Law states that if n markets exist and n – 1 markets are in equilibrium, then the nth market must also be in equilibrium. Technically, one market cannot be out of equilibrium while the other markets remain in equilibrium. To illustrate the concept of simultaneous equilibrium in multiple markets, however, we will consider the simultaneous adjustments that occur to restore general equilibrium when one market is thrown out of equilibrium in our simple model of three financial markets. To explore how these markets adjust, let’s consider what happens when all three markets begin in equilibrium, but then an exogenous shock causes equilibrium in the money market to be disrupted. For example, suppose that the Fed increases the money supply. In this case, the money supply curve shifts to the right, as shown in Figure 15.12 (b).
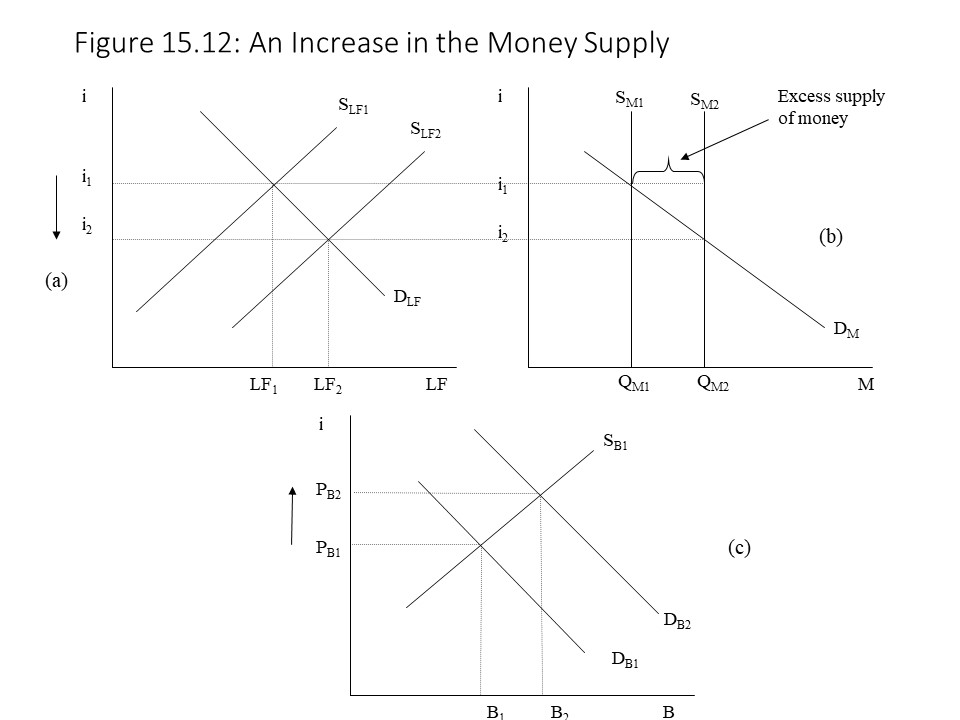
As the reader can see, the rightward shift of the money supply curve creates a surplus of money in the money market at the original interest rate, i1. That is, households and firms are now holding more money than they wish to hold at the current interest rate. As a result, they will use the surplus funds to buy bonds, thereby increasing the demand for bonds from DB1 to DB2 as shown in Figure 15.12 (c). The increased demand for bonds drives up the price of bonds towards its new equilibrium level. At the same time, the higher demand for bonds is equivalent to an increase in the supply of loanable funds, and so the supply of loans shifts from SLF1 to SLF2 as shown in Figure 15.12 (a). The interest rate falls towards its new equilibrium level of i2. As the interest rate falls in the loanable funds market, it also falls in the money market, and so an increase in the quantity demanded of money occurs, represented as a movement along the money demand curve. This movement continues until the money market is also in equilibrium. The result is simultaneous equilibrium in all three markets.
Now let’s return to the initial situation of equilibrium in all three markets, but this time let’s suppose that the Fed reduces the money supply, shifting the money supply curve to the left, as shown in Figure 15.13 (b).
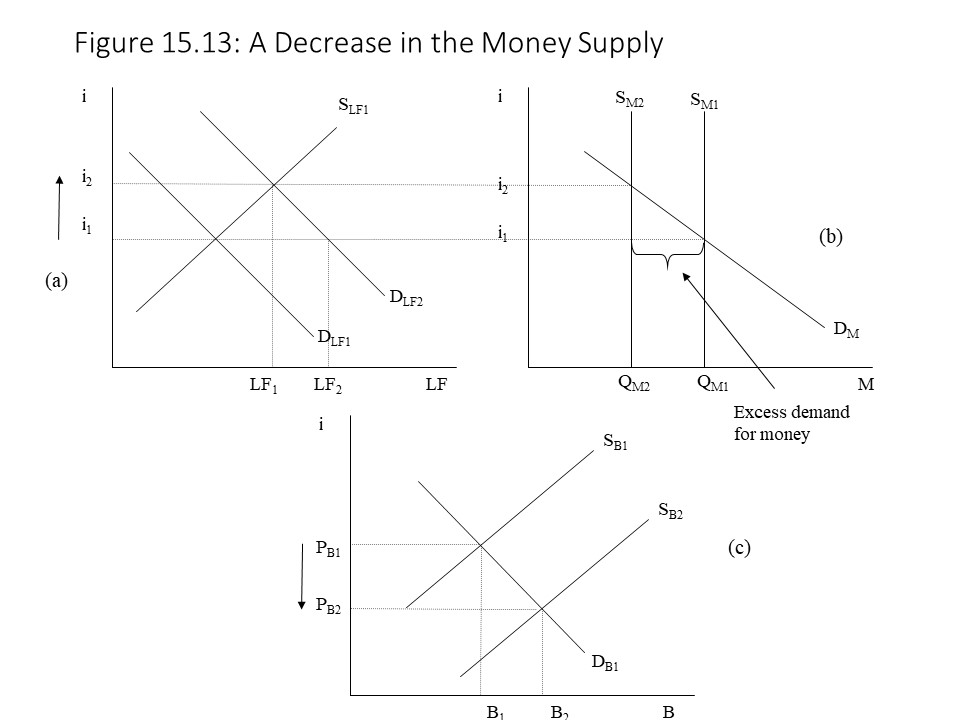
This time the leftward shift of the money supply curve creates a shortage of money in the money market at the original interest rate, i1. That is, households and firms are now holding less money than they wish to hold at the current interest rate. As a result, they will attempt to acquire funds by selling bonds, thereby increasing the supply of bonds from SB1 to SB2 as shown in Figure 15.13 (c). The increased supply of bonds drives down the price of bonds towards its new equilibrium level. At the same time, the higher supply of bonds is equivalent to an increase in the demand for loanable funds, and so the demand for loans shifts from DLF1 to DLF2 as shown in Figure 15.13 (a). The interest rate rises towards its new equilibrium level of i2. As the interest rate rises in the loanable funds market, it also rises in the money market and so a decrease in the quantity demanded of money occurs, represented as a movement along the money demand curve. This movement continues until the money market is also in equilibrium. Again, the result is simultaneous equilibrium in all three markets.
Once again, let’s return to the initial situation of equilibrium in all three markets, but this time let’s suppose that money incomes increase so that the demand for money rises. In this case, it is a rightward shift of the money demand curve that occurs as shown in Figure 15.14 (b).
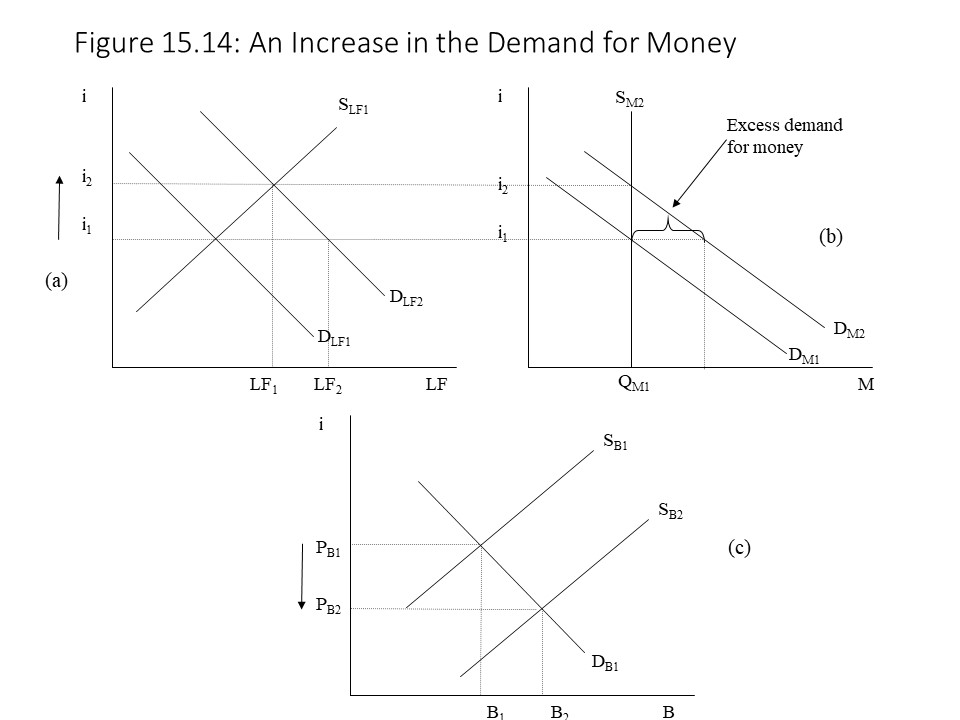
In this case, a rightward shift of the money demand curve creates a shortage of money in the money market at the original interest rate, i1. That is, households and firms are now holding less money than they wish to hold at the current interest rate. As a result, they will attempt to acquire funds by selling bonds, thereby increasing the supply of bonds from SB1 to SB2 as shown in Figure 15.14 (c). The increased supply of bonds drives down the price of bonds towards its new equilibrium level. At the same time, the higher supply of bonds is equivalent to an increase in the demand for loanable funds, and so the demand for loans shifts from DLF1 to DLF2 as shown in Figure 15.14 (a). The interest rate rises towards its new equilibrium level of i2. As the interest rate rises in the loanable funds market, it also rises in the money market, and so a decrease in the quantity demanded of money occurs, represented as a movement along the money demand curve. This movement continues until the money market is also in equilibrium. Again, the result is simultaneous equilibrium in all three markets.
Finally, let’s return to the initial situation of equilibrium in all three markets, but this time let’s suppose that money incomes decrease so that the demand for money falls. In this case, it is a leftward shift of the money demand curve that occurs as shown in Figure 15.15 (b).
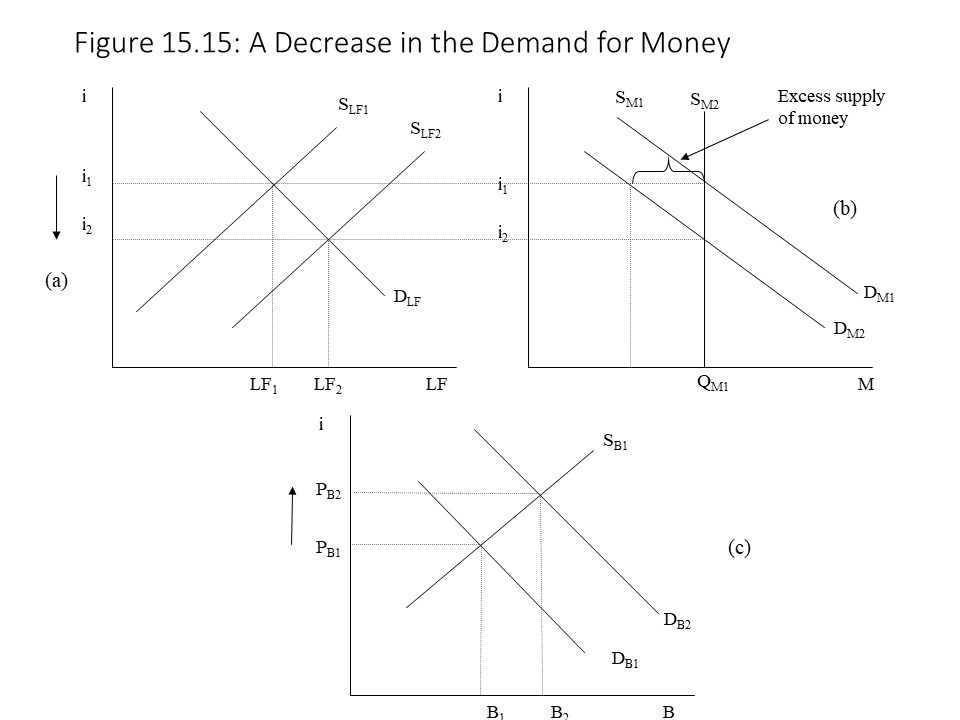
In this case, the leftward shift of the money demand curve creates a surplus of money in the money market at the original interest rate, i1. That is, households and firms are now holding more money than they wish to hold at the current interest rate. As a result, they will use their surplus funds to purchase bonds, thereby increasing the demand for bonds from DB1 to DB2 as shown in Figure 15.15 (c). The increased demand for bonds drives up the price of bonds towards its new equilibrium level. At the same time, the higher demand for bonds is equivalent to an increase in the supply of loanable funds, and so the supply of loans shifts from SLF1 to SLF2 as shown in Figure 15.15 (a). The interest rate falls towards its new equilibrium level of i2. As the interest rate falls in the loanable funds market, it also falls in the money market, and so an increase in the quantity demanded of money occurs, represented as a movement along the money demand curve. This movement continues until the money market is also in equilibrium. As before, the result is simultaneous equilibrium in all three markets.
All the cases considered clearly show that any disruption in the money market will lead to adjustments in the bond and loanable funds markets to restore equilibrium in all three markets. The analyses are also consistent with the general observation that bond prices and yields are inversely related, and with the money market in equilibrium, all firms and households are holding precisely the amount of money that they desire to hold, given their total assets.
Incorporating the Stock Market into the Analysis
At this stage, it should be clear how interest rates are explained within the neoclassical framework. Households and firms compare their actual money holdings with their desired money holdings and then buy or sell bonds when any discrepancies exist. Eventually, the rate of interest adjusts, which brings desired money holdings into line with actual money holdings. No surpluses or shortages exist in any of the financial markets, and the situation will persist unless an external shock disrupts the general equilibrium.
One financial market that has not been incorporated into the analysis thus far is the stock market. Just like with bonds, corporations issue shares of stock in order to raise funds. Unlike bonds, however, stocks are shares of ownership in the corporations that issued them. For example, Microsoft sells stock to the public. When a corporation sells stock to the public for the first time, it typically hires an investment bank, like Goldman Sachs or Morgan Stanley, to underwrite the stock issue. That is, it guarantees Microsoft a price per share and then sells it to the public in the primary market, pocketing a promoter’s profit in the process.
The buyer of Microsoft stock becomes a part-owner of the corporation and thus has a partial claim to the net income and assets of the firm. If the firm fails, the stockholder loses her investment. If the firm makes profits, then the stockholder may receive profit distributions in the form of dividends. The stockholder might also decide to sell the stock in the secondary market, such as the New York Stock Exchange. If the price of the stock has increased since the time it was purchased, then the stockholder will enjoy a capital gain upon selling it.
One of the benefits of stock ownership is the right to participate in shareholders’ meetings and to vote in elections that will decide the corporation’s board of directors. The possibility of large dividends and capital gains also makes stock ownership attractive, but losses may be considerable as well, and so stocks are generally rather risky. Another downside to stock ownership is that bondholders have a prior claim to the assets of the firm. If the firm fails, then the stockholders will be the last individuals to receive a share of the failing firm’s remaining assets.
Because many different companies issue their own stocks, when we refer to the stock market, we are referring to the market for many different financial assets. Just like we simplified our analysis in the previous section by referring to the bond market as the market for a single type of bond (even though many different types of bonds exist), we will discuss the stock market as the market for a single stock. Because bond prices tend to rise and fall together and stock prices tend to rise and fall together, many economists are comfortable developing theories without letting these differences stand in the way.
For simplicity, let’s suppose that a share of stock may be purchased at a price PS. To further simplify, let’s assume that annual dividend payments are expected for the next five years but that the firm will cease to exist at the end of that time period. If the annual expected dividend payments are D for the next 5 years, then we can write an equation that allows us to determine the discount factor (d) for the stock in the following way:[5]
A strong similarity exists between this formula and the one used to determine the yield on a five-year bond. The key difference here is that the dividend payments are not guaranteed but only expected. That is, a bondholder knows the interest payments that she will receive (if the corporation does not default on the payments, which means it fails to pay the bondholder). For the stockholder, the payments are much less certain. They may be higher or lower than D. They may be suspended if the Board of Directors decides that reinvestment of the firm’s profits is a superior move. Any number of factors might disrupt the payment of these expected dividends. As a result, stocks are inherently riskier than bonds and stockholders demand a premium to compensate them for this additional risk. The discount factor, is therefore, higher than the interest rate that we used to discount the interest payments associated with a bond. The discount factor applied to stocks (d*), in other words, will be the interest rate on bonds (i*) plus some additional amount to compensate for risk (i.e., a risk premium). That is, d* > i*. If the annual expected dividend payments (D) equal the fixed interest payments (A) on a bond issued by the same company (i.e., D = A), then the price of the stock will be lower than the price of the bond. That is, PS < PB. In other words, other factors the same, a stock should have a lower price than a bond due to its greater risk. The expected yield for the stock would then be higher than the yield on the bond. For this reason, stocks are generally viewed as potentially more lucrative than bonds.
To represent this situation graphically, we may consider the supply and demand for bonds and the supply and demand for stocks. Because stocks are riskier, having uncertain dividend payments, the demand for stocks will be lower than the demand for bonds. The equilibrium price of stocks (PS*) will, therefore, be lower than the equilibrium price of bonds (PB*), as shown in Figure 15.16, assuming other factors are the same, such as the expected payments associated with each asset.
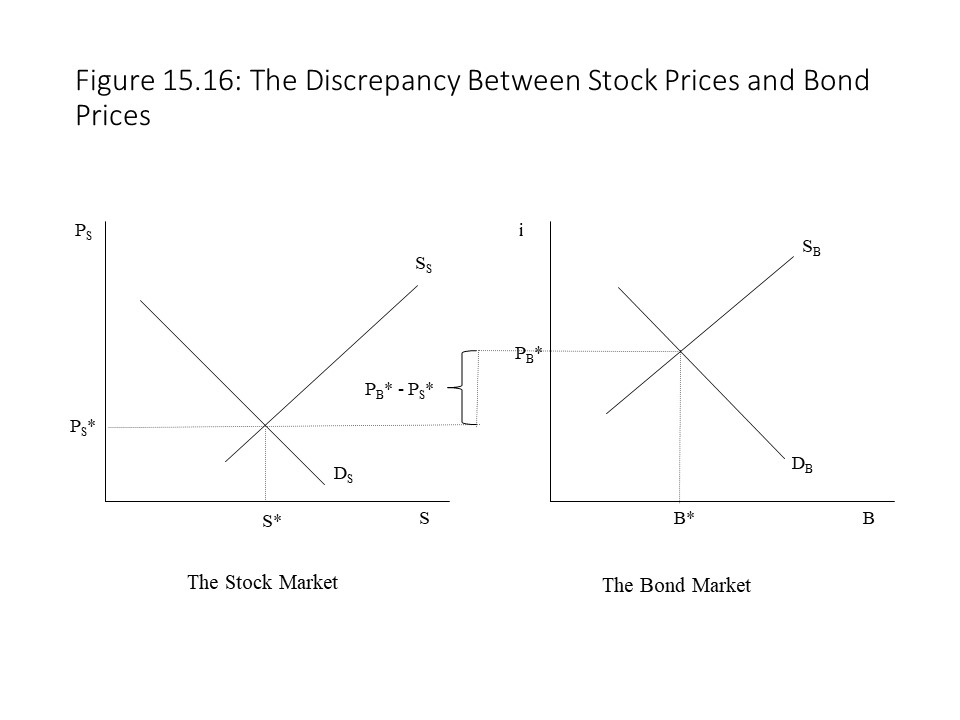
One might expect this situation to be temporary. If stocks are cheaper, then bondholders might be expected to sell their bonds and buy stocks instead. If bondholders behave in this way, then bond prices will fall and stock prices will rise until they are equal. This result will not occur, however, because the price differences are driven by the lower demand for stocks due to their greater perceived risk. The equilibrium is, therefore, stable, and the price discrepancy (PB* – PS*) will persist if the perceived degree of riskiness of the stock does not change.[6]
R eal Interest Rates v ersus Nominal Interest Rates
One additional aspect of the neoclassical theory of interest rates that deserves attention is the neoclassical distinction between nominal interest rates and real interest rates, which was introduced in Chapter 12. The nominal interest rate is the interest rate that is actually observed in the marketplace. As stated previously, many different interest rates are observed in the marketplace, and each interest rate is a nominal interest rate. Because these nominal interest rates tend to move together over time, economic theories frequently refer only to the nominal interest rate.
The real interest rate, on the other hand, refers to the interest rate corrected for inflation. For example, suppose that you lend $100 to someone at a 5% nominal rate of interest. In one year, your money will have grown to $105. If the prices of goods have increased in the meantime, however, then the purchasing power of your money may not have increased at all. The purchasing power of money refers to its real value, or the amount of actual goods it can purchase. The real interest rate then refers to the percentage increase in the purchasing power of a sum of money during the period of a loan.
To calculate the real interest rate, we assume that a sum of money (M) is loaned to an individual who is charged the nominal interest rate (i). We also assume that the general price level, as measured by the GDP Deflator or the Consumer Price Index (CPI), is denoted as P. The real value of M at the time the loan is made is M/P. For example, if M is equal to $10 and a specific type of apple priced at $0.50 each is the only good produced in the economy, then the real value of M is 20 apples (= $10/$0.50 per apple). Of course, when using a price index, the real value of the money will be stated in terms of constant base year dollars.
Now let’s suppose that M/P is loaned to a borrower. The real interest rate (r) will be the percentage change in M/P over the course of the year. The reader might know that when considering the percentage change in the ratio of two variables, it is possible to estimate the solution by subtracting the percentage change in the denominator from the percentage change in the numerator:
This shortcut method of calculating the real interest rate has a helpful interpretation. The percentage change in M is simply the nominal interest rate (i) that the borrower is charged. The percentage change in P is the rate of inflation (π). Therefore, the real interest rate may be calculated as follows:
That is, the real interest rate is simply the difference between the nominal interest rate and the inflation rate. Therefore, if $100 is loaned out for one year at a 5% nominal interest rate and the inflation rate for that year is also 5%, then the real interest rate is 0% (= 5% – 5%). That is, the rising price level completely wipes out the nominal increase in the sum of money, leaving the lender no better off and no worse off than before. Because of the tendency for inflation to wipe out the gains from lending, lenders will aim to charge a nominal interest rate that is high enough to cover the inflation rate and then allow for a positive real interest rate. Of course, the real interest rate will be determined competitively in the financial markets, as we have discussed.
The reader should note that it is possible for the real interest rate to be negative. Even if the nominal interest rate is 5%, the real interest rate will be -3% if the inflation rate is 8%. In that case, the lender will receive back a sum of money that is nominally larger than the amount originally loaned out (by 5%), but it will have 3% less purchasing power due to the high inflation rate.
An Austrian Theory of Interest Rate Determination
The neoclassical school of economic thought offers only one among several approaches to interest rate determination. The Austrian school of economics has also made important contributions to the theories of capital and interest. Eugene von Bohm-Bawerk developed a theory of capital in the late nineteenth century that served as a theory of interest rate determination. His theory was based on the physical productivity of capital whereas Ludwig von Mises in the early twentieth century focused more on the role of subjective preferences in the formation of the rate of interest. In this section, we will look at one way of representing Mises’s theory of interest within the context of a pure exchange economy. Because this theory can be developed without any reference to the theory of production, it serves as a straightforward introduction to the Austrian theory of interest.[7]
In developing his theory of interest, Mises relied heavily upon the concept of time preference. As described in Chapter 14, time preference refers to the fact that consumers have specific preferences regarding the time pattern of consumption. A consumer with a positivetime preference prefers to consume in the relatively near future as opposed to the relatively distant future. A consumer with a negativetime preference prefers to consume in the relatively distant future as opposed to the relatively near future. Finally, a consumer with a neutral time preference, or a time preference of zero, is indifferent between consuming in the relatively near future and the relatively distant future.[8] For example, suppose that three consumers have specific preferences regarding how many apples to consume in each of five periods of time. Table 15.1 represents the time preferences of the three consumers.
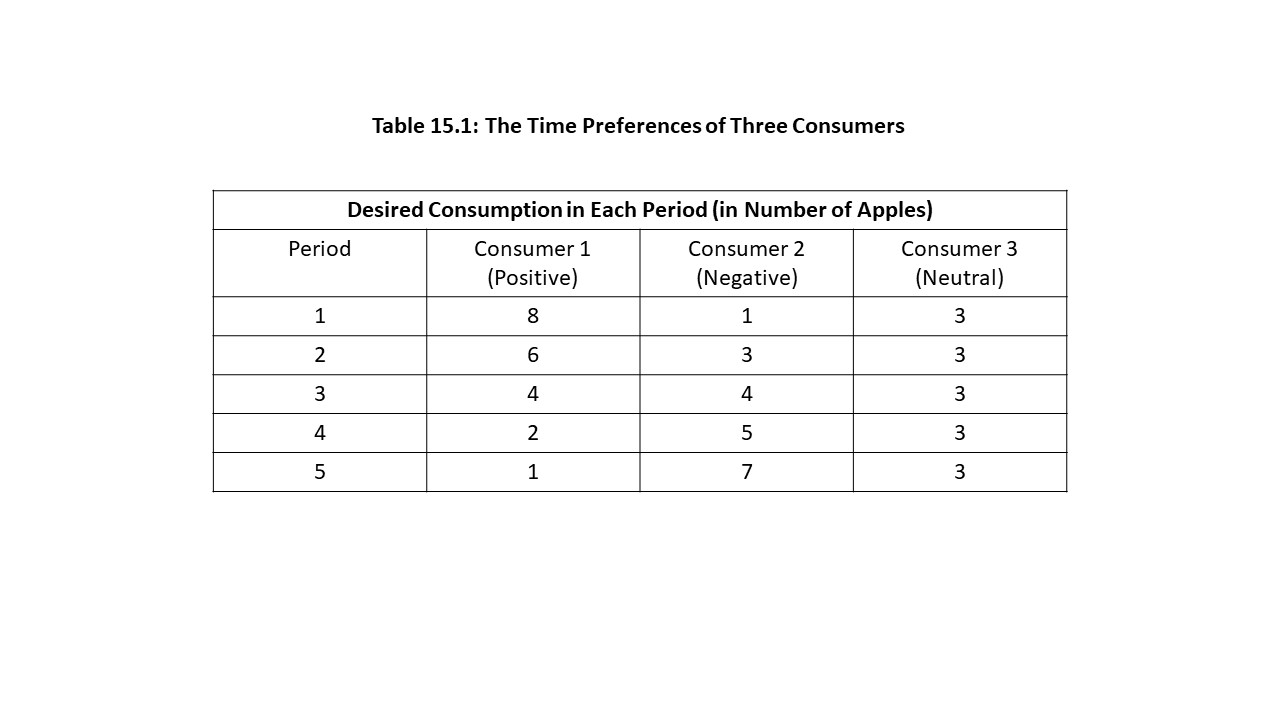
Clearly, consumer 1 has a positive time preference because she would like to consume more apples in the current period and in the relatively near future and fewer applies in the relatively distant future. Consumer 2 has a negative time preference. His desired consumption increases in the relatively more distant future periods. Finally, consumer 3 is comfortable consuming the same number of apples in every period regardless of when the apples will be consumed.[9] Although we can represent all of these cases, most consumers possess positive time preferences. That is, consumers prefer to consume now rather than later, but because these preferences are entirely subjective, negative and neutral time preferences are theoretically possible.
To further develop the Austrian theory of interest, let’s consider an example in which three consumers receive endowments of apples in each of seven periods with the first period representing the current period. Table 15.2 shows the time pattern of endowments for each of the three consumers over the course of the seven time periods.
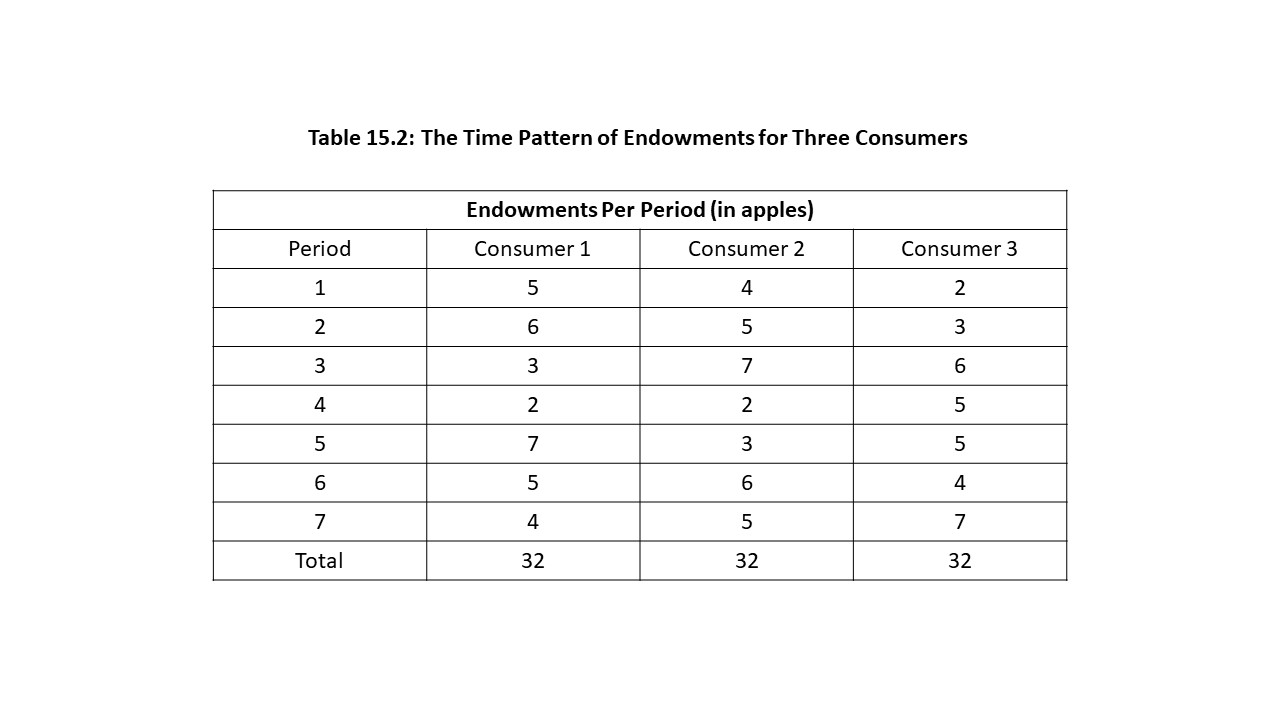
Of course, each consumer might have a time preference that differs substantially from their time pattern of endowments as shown in Table 15.3, which allows us to compare the time pattern of endowments with desired consumption for each consumer.

Rational people will try to bring their actual consumption into line with their desired consumption. If we assume zero storage costs, then a person with a negative time preference will be able to solve this problem herself. She simply needs to save her apples until later periods, assuming that the endowments are large enough in the periods closer to the present to allow for this plan to be executed. Since most people possess positive time preferences (like the three consumers in Table 15.3), however, consumers will typically want to transfer future apples to the time periods that are closer to the present. The problem is that apples cannot be transferred from the future to the present. A problem of time asymmetry exists. Time asymmetry means that present goods can be transferred to the future, but future goods cannot be transferred to the past.[10] The problem of time asymmetry means that consumers must find another method of increasing present consumption at the expense of future consumption. The way that consumers achieve this goal is by selling paper claims to their future apples to other consumers in the present. No consumer will pay one apple for a claim to one future apple because the consumer will gain nothing. A consumer will only give one apple in exchange for a paper claim to a future apple if the consumer is promised something extra as well. This something extra is called interest. Therefore, interest exists as a direct result of the presence of positive time preferences and the problem of time asymmetry. The market for paper claims to future production (i.e., the bond market) is also a direct result of subjective preferences for future goods.
To determine desired net borrowing for one consumer in a specific period, we only need to calculate the difference between her desired level of consumption and her endowment.[11] That is:
Desired Net Borrowing = Desired Consumption per Period – Endowment per Period
Table 15.4 shows the amount of desired net borrowing per period for each consumer. This amount of net borrowing is required for each consumer to achieve her desired consumption per period.

Table 15.4 shows that each consumer wishes to borrow in the current period and in the periods that are closer to the present time (for the most part). They would like to lend in the later periods as reflected in the negative desired net borrowings in the later periods. The problem that each consumer faces, however, is the constraint that the total consumption per period across all three consumers cannot exceed the total endowment per period for all three consumers. Trades of apples for paper claims can occur in a given period, but future apples cannot be received in the present. Any apples obtained above one’s endowment can only be the result of another consumer consuming an amount below her endowment. The situation depicted in Table 15.4 is impossible because the total desired consumption in period 1 is 27 apples, for example, but the total endowment in period 1 is only 11 apples. Therefore, this desired allocation is impossible. Another way of stating the same result is that the total actual net borrowing per period can never exceed zero. Any net borrowing must be balanced by net lending. In Table 15.4 desired net borrowing per period is positive for all three consumers. It is not possible for all three consumers to borrow in a specific period, and so these plans cannot be satisfied, and this ideal situation cannot arise.
The consumers resolve these difficulties to the best of their abilities by creating a bond market and supplying and demanding paper claims to future apples. The supply and demand for these paper claims will determine an equilibrium rate of interest. Let’s assume that this problem is resolved in all periods and that the interest rate is 100% in every period with all interest paid in the very last period. This assumption is a greatly simplifying assumption that allows us to represent one possible result. After all this haggling occurs, the actual consumption per period for each consumer will be determined as shown in Table 15.5.
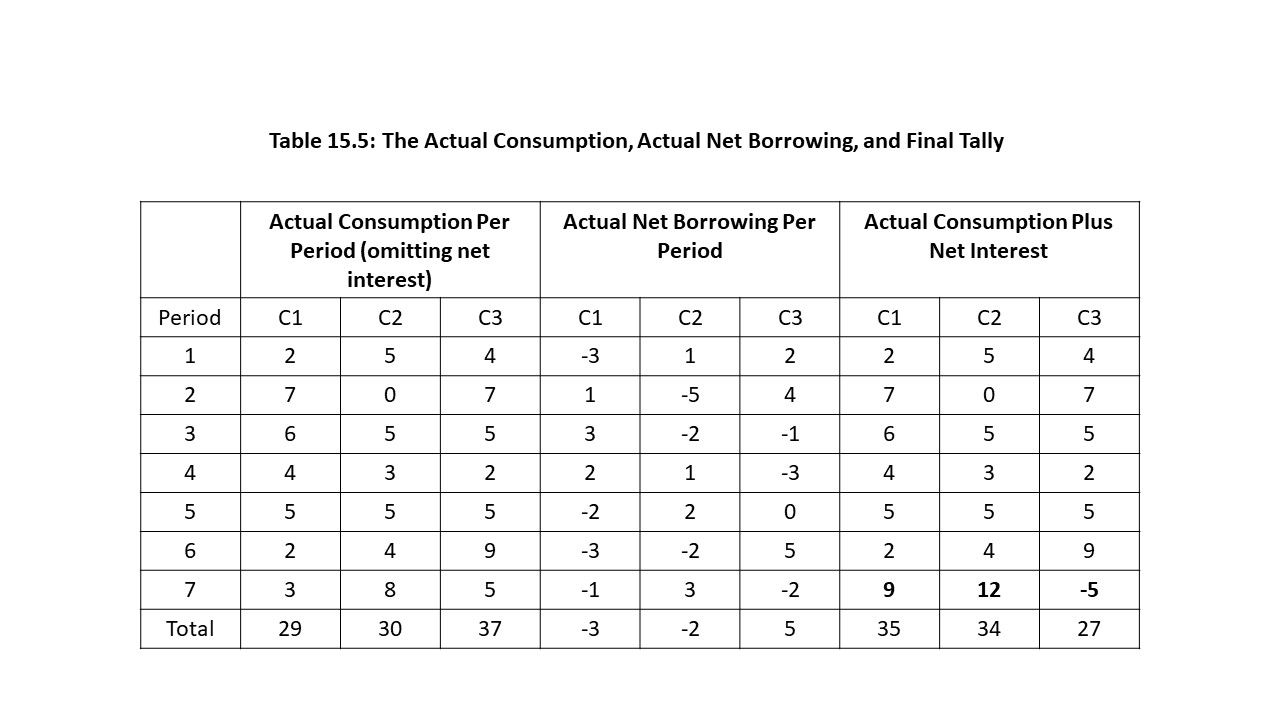
The actual consumption per period just represents a redistribution of the total endowment in each period across the three consumers. It is determined as the consumers decide whether to borrow or lend in each period. The actual net borrowing per period for each consumer can also be calculated as follows:
Actual Net Borrowing = Actual Consumption per Period – Endowment per Period
In this example, the total actual net borrowing per period is equal to zero in each period. Negative values for actual net borrowing indicate net lending and positive values indicate net borrowing. Table 15.2 shows that the aggregate endowment is 96 apples. In Table 15.5 the grand total for actual consumption is also 96 apples.[12] The final three columns of Table 15.5 also show how the receipt of net interest in the final period affects the final results. Because the interest and principal are paid in period 7, those numbers are indicated in bold. The bold numbers represent the only difference between actual consumption per period plus net interest and actual consumption per period omitting net interest, as shown in Table 15.5. Net interest is calculated as follows:
Net Interest = Principal and Interest Received – Principal and Interest Paid
For example, to calculate the net interest for consumer 1 in period 7, simply multiply 2 times 9 (=3+2+3+1) to obtain 18 apples. This amount is the principal and interest received. It is obtained by multiplying each apple loaned out by 2, shown as negative net borrowings for consumer 1. Remember the interest rate is assumed to be 100% and so the multiplication by 2 ensures that we account for principal and interest. Next determine the principle and interest paid by consumer 1. Multiply each apple borrowed by 2, shown as positive net borrowings for consumer 1. That is, multiply 2 times 6 (=1+3+2) to obtain 12 apples. Finally, using these results, add 3 apples of actual consumption (found in the column that omits net interest) to 18 apples (principal and interest received), and then subtract 12 apples (principal and interest paid). The result is 9 apples.
In the end, the total actual consumption plus net interest across all three consumers is equal to 96 apples. Hence, all apples in the initial endowment are reallocated across time to improve the situation of each consumer, although no consumer achieves their most desired allocation. It is also worth noting that consumers 1 and 2 experience negative net borrowings overall, which means they are net lenders. Consumer 3, on the other hand, is a net borrower with a positive total of actual net borrowings. What this means is that, once the net interest is paid, consumers 1 and 2 end up with a total number of apples in excess of their original endowments of 32 apples each. Consumer 3, on the other hand, ends up with 27 apples and thus consumes less than the total endowment.[13] The reason, of course, is that consumer 3 is a net debtor and must pay a fair amount in interest for consuming the most in the first three periods.
The model presented here takes certain liberties in extending Mises’s theory to illustrate a number of key points. The main point should be clear, however, which is that interest arises inevitably as a result of the different subjective time preferences of consumers. Because of the problem of time asymmetry, it is not possible for consumers to transfer future goods to the present. Hence, they engage in trade with one another in the present period and create a market for paper claims to future goods. A positive rate of interest is inevitable because otherwise no one would have an incentive to hand over present goods to another person. The rate of interest that results is determined competitively in the marketplace through a process of haggling. This representation of the Austrian theory of interest does not show how this process leads to the formation of a market rate of interest, but it does demonstrate that such a rate of interest arises because consumers seek to fulfill their consumption plans over time.
A Marxian Theory of Interest Rate Determination
Marxian economists also have ideas about how interest rates are determined. Karl Marx wrote about the formation of the rate of interest in Volume 3 of Capital, which was published after Marx’s death by his friend and collaborator Frederick Engels in 1894. In this section, we will examine one interpretation of Marx’s interest rate theory.[14]
In Marxian economics, the rate of interest is related in a logical way to the rate of profit (p) and another rate that Theodore Lianos calls the rate of profit of enterprise (re). To demonstrate the relationship between these three rates, it is necessary to begin with an identity. That is, aggregate profit (P) in the economy is identically equal to aggregate interest (I) plus aggregate profit of enterprise (Re) as follows:
In other words, capitalist enterprises possess a total amount of profit, part of which is used to pay interest for the use of borrowed money capital. The other part is profit kept by the enterprise for its own internal use or for distribution to shareholders. The next step is to divide both sides by the aggregate capital, which consists of variable capital (V) and constant capital (C) as follows:
Next we multiply each expression on the right hand side of the equation by ratios that are equal to 1, thus maintaining the equality. That is:
A in this equation refers to the total borrowed money capital. Therefore, C+V–A refers to the total non-borrowed money capital. Rearranging the terms a bit yields the following result:
In this case, A/(C+V) refers to the fraction of the total capital that is borrowed. Similarly, (C+V-A)/(C+V) refers to the fraction of the total capital that is not borrowed. If we set k = A/(C+V), then the equation may be written as follows:
As is explained in Chapter 4, P/(C+V) represents the rate of profit for the economy as a whole. In Chapter 4, we defined the rate of profit as the aggregate surplus value divided by the total capital advanced. However, if values have been transformed into production prices, then it is more appropriate to refer to the ratio of aggregate profit to aggregate capital advanced. The expression I/A is the rate of interest. It is simply the amount of interest paid (received) divided by the amount of capital borrowed (lent). Finally, the expression Re/(C+V-A) is the rate of profit of enterprise. It is the profit of enterprise divided by the amount of non-borrowed money capital. Finally, k refers to the fraction of the total capital that is borrowed. If we substitute the symbols p for the rate of profit, i for the rate of interest, and re for the rate of profit of enterprise, then we have the following result:
This final expression states that the rate of profit is equal to a weighted average of the rate of interest and the rate of profit of enterprise where k and 1-k serve as the weights.
If we assume that the rate of profit is given, we can then represent all the combinations of the interest rate and the rate of profit of enterprise that are possible in a two-dimensional space. To do so, we solve the above expression for re as follows:
This equation turns out to be linear with a vertical intercept of p/(1-k) and a constant slope of –k/(1-k). Given the rate of profit, we can graph the equation as in Figure 15.17.

It should be clear that the interest rate and the rate of profit of enterprise are inversely related. That is, as the interest rate rises, the rate of profit of enterprise must fall, and vice versa. This negative relationship is reflected in the downward slope of the line.
More can be stated about the relationship between the three rates that we are considering. For example, consider the point at which the rate of interest and the rate of profit of enterprise are equal (i.e., re = i). If we draw a line through all the combinations of re and i where these rates are equal, then we obtain a positively sloped line with the equation re = i. The reader should note that this line has a slope of 1 and will rise at a 45-degree angle relative to the horizontal axis. The point at which this 45-degree line intersects the line that shows the relationship between i and re represents the unique point where re and i are equal given this profit rate.
If we set i = re and plug it into the equation of the line relating the two variables, then we obtain the following result:
If p = i, then it necessarily follows that p = re as well since i = re. All these results are captured in Figure 15.18.
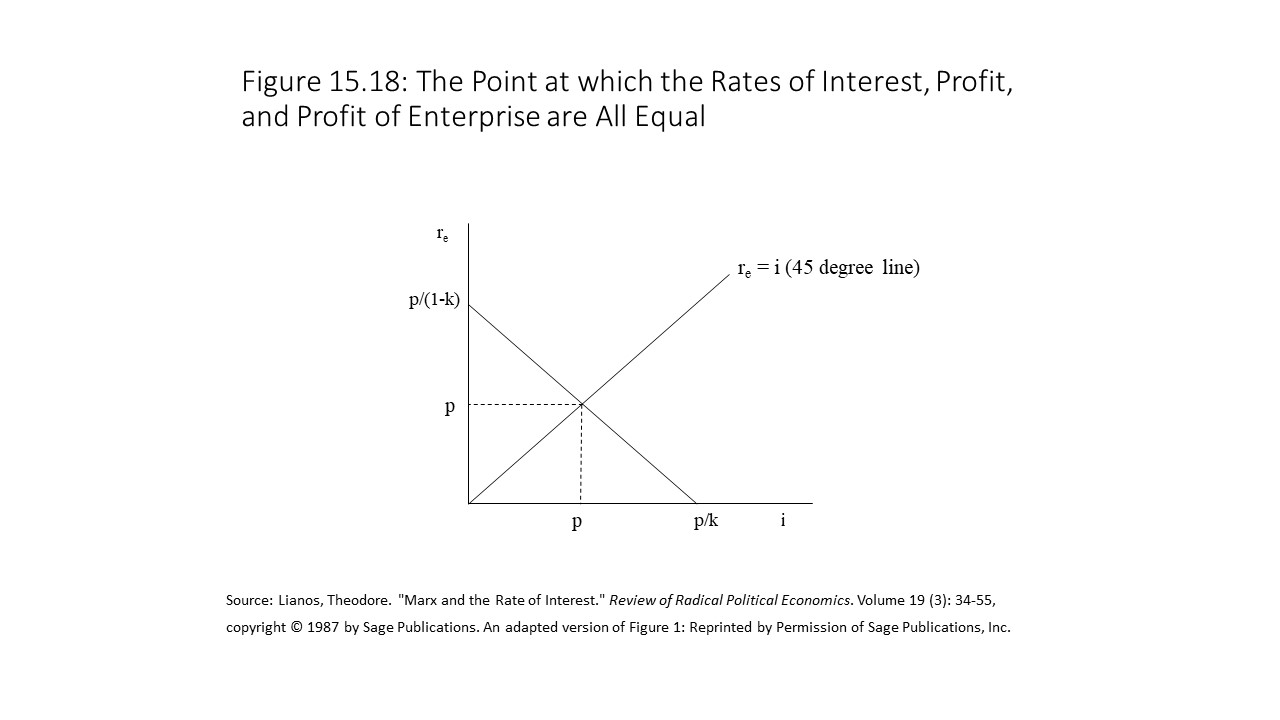
A few interesting results necessarily follow. If the economy is on the downward sloping line at a point above the intersection with the 45-degree line, then the following results must hold:
On the other hand, if the economy is on the downward sloping line at a point below the intersection with the 45-degree line, then the following results must hold:
This entire discussion has assumed a constant aggregate rate of profit (p). Over the course of the business cycle, however, the rate of profit fluctuates.[15] Because the vertical and horizontal intercepts of the downward sloping line depend on p, while the slope does not, it follows that parallel shifts to the right (during an expansion) and to the left (during a contraction) will occur over the course of the business cycle.[16]
If the rate of profit fluctuates in a way that can be explained, and the rate of interest fluctuates in a way that can be explained over the course of the business cycle, then fluctuations in the rate of profit of enterprise should be explainable as well using the equation of our downward sloping line.[17] That is, with the movements in two out of three variables explained, the third variable must be explained as well given the logical relationship between the three rates. In Chapter 14, we discussed the fluctuations in the rate of profit according to Marxian theory. Hence, our goal is to explain movements in the rate of interest, which will then complete the explanation of all three rates.
According to Marx, the rate of interest in a capitalist economy is competitively determined in the market for loan capital. This claim sounds rather similar to the neoclassical claim that the loanable funds market plays a central role in the determination of the rate of interest. A key difference exists, however, between Marx’s theory and the neoclassical theory. Unlike in neoclassical theory, changes in production are the key to interest rate fluctuations over the course of the business cycle. As output rises and falls, the demand for loan capital changes in response to the needs of industrial capitalists.[18] The degree of tightness in the money capital market then determines whether the interest rate rises and falls as well as the speed of the adjustments.[19]
To clarify the argument, let’s assume that the demand for loanable money capital is positively related to the level of production (i.e., output). Let’s also assume that the supply of loanable money capital is given or fixed. Both assumptions are reflected in Figure 15.19 (a).[20]

As output rises during an expansion, beginning at Q1, the quantity supplied exceeds the quantity demanded of loan capital. As a result, the interest rate declines as shown in Figure 15.9 (b). Because the gap becomes smaller between the two curves, the reduction in the interest rate is relatively slow. Once output rises beyond Q*, the demand for loan capital exceeds the supply, and the interest rate rises. Because the gap grows rapidly, the interest rate rises very quickly. After the level of output peaks at Q2, it begins to fall, indicating that a recession has begun. Since the quantity demanded still exceeds the quantity supplied, the rate of interest continues to rise but much more slowly because the gap is becoming smaller. Once output falls below Q*, the interest rate falls very quickly due to the rapid increase in the gap between the supply and demand for loanable funds. Once the trough of the recession is reached at Q1, it begins to rise once more with a new expansion, and the cycle begins again.[21]
Now that the movement of the rate of interest has been fully explained, this knowledge can be combined with what we know about the movement of the profit rate over the course of the business cycle and the identity that relates the profit rate, the interest rate, and the rate of profit of enterprise. All this information provides an explanation for the movement of the rate of profit of enterprise over the course of the business cycle. With the interest rate following the pattern in Figure 15.19 (b), we can expect the rate of profit of enterprise to fluctuate opposite the interest rate fluctuations given the negative relationship between the two rates.[22]
In closing, it is worth reflecting on the key differences between the Marxian and neoclassical theories of the rate of interest. First, the Marxian theory suggests that the level of production is the most important factor determining movements in the rate of interest, as opposed to the responses of borrowers and lenders to shortages and surpluses in the market for loanable funds.[23] Second, the Marxian theory is a disequilibrium theory of the rate of interest as opposed to its neoclassical counterpart. Even though a point exists (Q*) where both quantity supplied and quantity demanded are equal in the market for loan capital, the economy has no inherent tendency to move towards this point because the level of production is being driven by other factors.[24] Finally, the rate of interest in Marxian theory is linked to the rate of profit, and the rate of profit reflects how successful capitalists have been in terms of exploiting labor-power. That is, interest income is a portion of the aggregate profit, and aggregate profit is explained on the basis of the surplus labor performed by the working class. By contrast, in neoclassical theory, the rate of interest is the price paid for loanable funds, and the loanable funds market is the market that harmonizes the interests of savers who have a surplus of funds and borrowers who are short of funds. In other words, this market transfers funds from those who lack an efficient use for funds to those who have an efficient use for funds. In short, it is not only the mechanics of interest rate determination that differ across the two theories, it is also the social meaning of the interest rate and the market in which it is determined.
Following the Economic News [25]
In The Globe and Mail (Canada), Ian McGugan recently described changes in the Canadian and U.S. stock and bond markets. He describes the bond market as “gloomy” and the stock market as “still largely upbeat.” McGugan notes that the markets are sending signals that provide conflicting messages about the likelihood of a U.S. recession. The high share prices, for example, suggest optimism about future economic prospects. The gloomy bond market suggests the opposite. McGugan explains that the bond market has recently become much more pessimistic. The pessimism, McGugan argues, is reflected in a recent increase in bond prices and falling bond yields due to “investors’ newfound eagerness to buy bonds.” That is, a higher demand for bonds has pushed up the prices of U.S. Treasury bonds and pushed down the interest rates on U.S. Treasury bonds. This “flight to safety” is expected when investors are pessimistic about the future and anticipate a recession and a falling stock market. McGugan explains that this shift in investor sentiment is occurring on a global scale. Citing Bloomberg data, McGugan explains that “[n]early US$11 trillion worth of bonds around the world are now yielding below zero per cent,” which represents the largest volume of bonds with negative interest rates since 2016. The negative interest rates suggest that the demand for these safe-haven bonds is so high that their market prices are producing negative yields. For example, a Treasury bill with a negative interest rate would sell for a price that exceeds its face value. An investor would purchase it at a price that is higher than the amount received in the future, which translates into a negative interest payment. As McGugan explains, “an enormous amount of money is now being bet on the proposition that it’s better to own bonds, even at negative rates, than to take on stock market risk in a slowing global economy.” Due to strong recent corporate earnings, however, McGugan argues that the relative calmness of the stock market makes sense. Nevertheless, McGugan explains that eventually “stocks will feel the pain if the bond market is right about slowing economic growth.” In that scenario, the demand for stocks will fall as the demand for bonds continues to rise. Bond prices will rise relative to stock prices as our supply and demand models of the stock and bond markets indicate.
Summary of Key Points
- To calculate the future value (FV) of a sum of money, it is necessary to multiply the present sum by (1+i)n. To calculate the present value (PV) of a sum of money, it is necessary to divide the future sum by (1+i)n.
- To calculate the present value of a bond, it is necessary to add up the present value of each future payment associated with the bond.
- Interest rates and bond prices are always inversely related.
- The demand for loanable funds is equivalent to the supply of bonds, and the supply of loanable funds is equivalent to the demand for bonds.
- In equilibrium, the price of a bond is equal to its present value.
- The money market is not the market for short-term securities but the market in which discrepancies between actual money holdings and desired money holdings influence the rate of interest.
- The three components of money demand are the transactions demand, the precautionary demand, and the asset demand for money.
- In the neoclassical model of interest rate determination, competition causes the loanable funds market, the bond market, and the money market to all clear simultaneously, leading to a general equilibrium.
- Other factors the same, an equilibrium stock price will be lower than an equilibrium bond price due to the greater risk and uncertainty of dividend payments associated with the stock.
- The real interest rate is calculated as the nominal interest rate minus the rate of inflation.
- In Austrian theory, a positive rate of interest emerges because consumers have different time preferences and because the problem of time asymmetry exists.
- In Marxian theory, changes in the level of production lead to changes in the degree of tightness in the loan capital market, which then lead to fluctuations in the rate of interest.
List of Key Terms
Rate of interest
Principal
Compound interest
Future value
Present value
Discounted
Bond
Coupon bonds
Term to maturity
Yield to maturity
Loanable funds market
Equilibrium interest rate
Equilibrium quantity of loanable funds
Bond market
Equilibrium bond price
Equilibrium quantity of bonds
Money market
Money market instruments
Money
Liquidity
Actual money holdings
Demand for money
Transactions demand for money
Precautionary demand for money
Capital gain
Speculative demand for money
Asset demand for money
General equilibrium model
Partial equilibrium model
Marginalist revolution
Walras’s Law
Stocks
Underwriting a stock issue
Primary market
Promoters’ profit
Dividends
Secondary market
Default
Nominal interest rate
Real interest rate
Purchasing power
Time preference
Positive time preference
Negative time preference
Neutral time preference
Time asymmetry
Profit of enterprise
Rate of profit
Rate of profit of enterprise
Problems for Review
- Suppose you lend $250 for two years at an annual interest rate of 6.5%. What is the future value of your loan at the end of year 2?
- Suppose you purchase an asset that will pay you $1000 in three years. If the annual interest rate is 3.5%, then what is the present value of your asset?
- Suppose you buy a bond that will pay you $300 per year for the next four years. If the annual interest rate is 4%, then what is the price of your bond if the market is in equilibrium?
- Suppose you purchase a stock that is expected to pay a dividend of $300 per year for the next four years. If the discount rate is 5.5%, then what is the stock price in this case? Is this result the one you would expect when comparing this answer to the one you obtained in question 3? Why or why not?
- Assume that the loanable funds market, the bond market, and the money market are all in equilibrium. What will happen if the central bank reduces the money supply? Explain what occurs in the money market and how these changes lead to additional changes in the bond and loanable funds markets.
- Suppose that you lend money at an annual interest rate of 12% and the annual inflation rate is 7%. What is the real interest rate that you earn?
- What is the actual net borrowing of a consumer if the actual consumption in a period is 6 apples and the endowment in that same period is 8 apples? What does the sign of your answer imply?
- Suppose the rate of profit is 50% and the proportion of capital borrowed by industrial capitalists is 75%. Write the equation of the line that relates the rate of profit of enterprise to the rate of interest. Next draw a graph of this line in a space with the rate of profit of enterprise on the vertical axis and the rate of interest on the horizontal axis. Label the horizontal and vertical intercepts as well.
- See Mankiw (1997), p. 58, for a justification of references to “the interest rate.” ↵
- Mishkin (2006), p. 105, footnote 4, emphasizes this point. ↵
- McConnell and Brue (2008), p. 260, present the transactions demand for money as a vertical line. This presentation adds the precautionary demand as a second source of money demand that is independent of the interest rate. ↵
- For example, Samuelson and Nordhaus (2001), p. 520-521, and McConnell and Brue (2008), p. 259-261, focus on the transactions demand and the asset demand for money only. Mishkin (2006), p. 521-522, on the other hand, concentrates on the transactions, precautionary, and speculative motives for holding money. ↵
- Mishkin (2006), p. 143, includes a similar formula for the calculation of a stock price. Mishkin, however, includes a final term representing the final sales price of the stock at the end of the holding period. It is omitted here just as the face value of the coupon bond (i.e., the return of the principal) was omitted in our discussion of how to calculate the present value of a coupon bond. ↵
- A similar argument can be used to explain the risk structure of interest rates. See Mishkin (2006), p. 120-127. ↵
- The model presented in this section uses as a starting point the interpretation of Mises’s theory of interest as presented in Moss (1978), p. 157-166. Nevertheless, certain liberties have been taken for ease of exposition. ↵
- Moss (1978), p. 161, attributes the distinction between positive, negative, and neural time preferences to economists Irving Fisher and Gary Becker. ↵
- See Moss (1978), p. 161, where he states that “an individual satisfied with an equal number of apples in each time period is said to display neutral or zero time preference.” ↵
- See Moss (1978), p. 163-164, for an explanation of the asymmetry in the time market. ↵
- Moss (1978), p. 160, defines net borrowing as the difference between desired consumption and the endowment. ↵
- Moss (1978), p. 163, states that “total apple consumption for the entire society must equal total apple endowment when both totals are summed over all individuals and all periods.” ↵
- Moss (1978), p. 163, explains that it is possible “for a single individual’s total n-period consumption to be greater or less than his total aggregate apple endowment. Whether it will be greater or less depends, of course, on whether over the n periods he was a net interest payer or receiver.” ↵
- The interpretation that is discussed in this section was developed by Lianos (1987). Aside from a few notational changes, the mathematical presentation in this section is found in Lianos’s original article. The original source for this material is: Lianos, Theodore. "Marx and the Rate of Interest." Review of Radical Political Economics. Volume 19 (3): 34-55, copyright © 1987 by Sage Publications. Adapted versions of Figures 1, 4, and 5 with equations 1-6: Reprinted by Permission of Sage Publications, Inc. ↵
- Lianos (1987), p. 36. ↵
- Lianos (1987), p. 37, shows these parallel shifts in his Figures 1 and 2. ↵
- Lianos (1987), p. 38, shows how the rate of profit of enterprise and the rate of interest fluctuate relative to one another in his Figure 3. ↵
- Lianos (1987), p. 45. ↵
- Lianos (1987), p. 45-46. ↵
- The graphs in Figure 15.19 have been re-created using Figures 4 and 5 in Lianos (1987), 46-47. ↵
- Ibid. p. 46-47. ↵
- Lianos (1987), p. 37-38, describes the complicated relationship between the two rates throughout the business cycle. ↵
- As Lianos (1987), p. 52, puts it, “the real sector dominates the monetary sector.” ↵
- Lianos (1987), p. 52, states that the “differences between demand and supply create equilibrating tendencies but they do not lead to equilibrium and stability of the interest rate, because the moving force in this model is the process of accumulation and income growth.” ↵
- McGugan, Ian. “Opinion; With bond market gloomy, why are stocks still near record levels?” The Globe and Mail (Canada), Ontario Edition. 30 May 2019. ↵


