16: Money Supply Measures and Theories of Commercial Bank Behavior
- Last updated
- Save as PDF
- Page ID
- 46264
Goals and Objectives:
In this chapter, we will do the following:
- Identify what most economists consider to be the traditional functions of money.
- Define several different types of money
- Distinguish between the Neoclassical and Austrian Measures of the Money Supply
- Examine the difference between 100% reserve banking and fractional reserve banking
- Explore the different items on a commercial bank’s balance sheet
- Investigate the neoclassical theory of banks and its link to the theory of financial markets
- Develop a Marxist theory of banks and link it to the theory of financial markets
In Chapter 15, we explored three theories of financial markets. Our focus was on the way in which financial markets determine the rate of interest and cause fluctuations in the rate of interest over time. Our purpose in this chapter is to incorporate the role of money into our neoclassical and heterodox analyses. Therefore, this chapter explores the topic of money, including its functions, major types, and most important measures. How to measure money is somewhat tricky, and neoclassical and Austrian economists do not agree on the best method of measuring its total quantity. This chapter also discusses the banking system, which is closely connected to the subject of money and its amount. A financial statement known as a balance sheet is introduced in this chapter so that it is easier to explore the way commercial banks’ activities alter their financial positions and affect the quantity of money in the economy. This background makes it possible to compare two competing theories of how commercial banks operate and how they influence the financial markets. The final part of the chapter, therefore, contrasts the neoclassical and Marxist theories of commercial bank behavior and how those theories connect to the neoclassical and Marxist theories of financial markets discussed in Chapter 15.
The Traditional Functions of Money [1]
When neoclassical economists define money, they do not associate it with any specific object but rather with the functions that it fulfills. In other words, if an object fulfills certain functions, then it is regarded as money. If it does not fulfill these functions, then it is not money. The first function of money is medium of exchange. To understand this function, it helps to think about a barter economy. A barter economy is an economy in which no money exists and commodities are exchanged for other commodities. For example, five textbooks might exchange for one desk. Barter economies allow owners of commodities to trade for the commodities that they want, but they face one major problem that is referred to as the double coincidence of wants problem. For example, suppose that I have five textbooks and would like to purchase one desk. To make this trade, I need to find someone who has a desk to sell. The problem that arises for me, however, is that this person must also want my textbooks if the trade is to occur. For our wants to exactly coincide in this manner would require a double coincidence: the desk owner wants what I have and I want what the desk owner has. If money is introduced into this economy, then the problem is solved. Why? Money by its nature is universally regarded as valuable. Even if the desk owner does not want my textbooks, the desk owner will be pleased to accept my money because it can be used to purchase something else that the desk owner wants, such as a painting, from someone else. That is, money serves as a medium of exchange. It facilitates exchange by making possible the exchange of the desk for the painting, even though this exchange does not occur directly. With money regarded as universally valuable, now I only need to find someone with the commodity that I wish to buy (assuming I have sufficient money to pay the price), and the double coincidence of wants problem is solved.
It should now be clear why neoclassical economists regard money as a means of increasing efficiency. The time required to find someone with whom to make a trade in a barter economy is much greater than the time required in a monetary economy. Because money cuts down on the time required to find someone with whom to make a trade, that freed up time can be used for more productive activities.[2] Also, because of the double coincidence of wants problem, people in barter economies do not want to rely so much on market exchange. It is risky to do so because of the difficulties associated with finding people with whom to trade. In a monetary economy, by contrast, people feel much more comfortable relying on market exchange. As a result, producers specialize more because they know that they can easily sell their products and services for money, which can be used to obtain other commodities they really desire.[3] Specialization and division of labor, of course, greatly increase labor productivity. With greater productivity and overall production, it is easy to see that money makes possible a higher level of efficiency.
A second function that neoclassical economists associate with money is its role as unit of account. According to this function, money provides a standardized unit by which to measure prices. That is, money provides a gauge for measuring value. With a standardized unit, it becomes possible to make fine distinctions in the values of commodities. Comparisons of value then become easier to make, which aids decision making. The divisibility of the object is thus of crucial importance. Historically, precious metals like gold and silver, have served as money. Metallic substances can be melted down, weighed, and transformed into standardized units, such as bars and coins. It is important to remember, however, that just because an object can serve as a unit of account, it also must be able to fulfill the other functions of money. If it fails to fulfill the other functions, then societies will reject it for the role of money. For example, milk can be easily measured and careful distinctions in value could be determined if all prices were stated in terms of ounces of milk. Milk does not serve well as a form of money, but it is not because it fails as a unit of account. It fails because it does not fulfill the third function well at all.
The third function that neoclassical economists associate with money is its role as a store of value. As a store of value, money makes it possible to transfer purchasing power from the present to the future. To succeed in this role, the object must be highly durable. An object that spoils or corrodes over relatively short time periods will not maintain its value in exchange. Precious metals are highly durable. Milk, on the other hand, spoils after a short time and so if wealth is held in this form, it will quickly vanish and the owner will lose all claim to future commodities.
If all three functions are fulfilled by an object, then neoclassical economists regard the object as money. Societies also tend to use such objects as money because people have recognized, even if not explicitly, the important role that each of these functions serves. Marxian economists also recognize the importance of these functions although the language used is somewhat different (e.g., means of circulation, measure of value, object of hoarding).[4] One important difference between the Marxian and neoclassical analyses of these functions deals with the unit of account (or measure of value) function. Neoclassical economists regard the unit of account function as important because it makes it possible to compare prices of commodities using a common unit. Marxian economists take it further, however, with the argument that money serves as the universal expression of homogeneous human labor. That is, money does not just make it possible to compare the prices of commodities using a common unit, which it certainly does. It also serves as the object through which socially necessary abstract labor time is expressed within the capitalist mode of production. When money serves as a means of circulation (or medium of exchange) as represented in a commodity circuit (C-M-C’), it renders the socially necessary abstract labor time embodied in the two commodities (C and C’) commensurable. That is, the embodied SNALT is regarded as equal in the two commodities, and it is regarded as equal to the SNALT embodied in (or reflected in) the money commodity.
Different Types of Money: From Mollusk Shells to Bitcoins
Throughout history many different objects have fulfilled the functions of money to a greater or lesser extent. The form of money that was used for the longest period throughout human history is the cowrie, which is a mollusk shell found in the Indian Ocean.[5] For more than 2,000 years, it served as money at various times in China, India, Europe, and Africa. Many other commodities have circulated as money, including stone wheels, gold, silver, copper, and cigarettes. Each commodity is considered commodity money because it circulates as money and yet has some intrinsic value or alternative use. For neoclassical economists, the alternative use of the commodity justifies the label. For Marxian economists, commodity money is also the product of socially necessary abstract labor time, which renders its value in circulation comprehensible.
A more recent form of money is convertible paper money. When people refer to the gold standard, for example, they have in mind convertible paper money. During the nineteenth century, for example, commercial banks would issue paper notes that represented claims to their gold reserves. The holder of the paper notes could use the notes to pay bills and settle debts, and the paper was “as good as gold.” The U.S. government also printed paper notes that represented claims to gold. Eventually, the U.S. Federal Reserve would issue paper notes that were identified as Federal Reserve Notes, representing the debt of the issuer. That is, the holder possessed a claim to the assets of the central bank. As late as the mid-twentieth century, some U.S. notes were still redeemable for precious metals and so were backed by commodity money. After World War II, gold reserves continued to back U.S. dollars used in international transactions. The international gold standard was abandoned, however, in the 1970s.
If convertible paper money is no longer available, then what kind of money do we have? We now have inconvertible paper money. That is, we have paper money that is not convertible into anything else. It cannot be exchanged at any bank for gold, silver, copper, or any other commodity money. Why do people hold money if it is not redeemable into any commodity of value? People hold money because the government has declared it to have value. Because it is declared to be money by government decree, it is labeled fiat money. To some extent, the value of fiat money represents people’s faith in the government. The more important reason that people hold money, however, is that it is generally accepted in exchange for other commodities. People understand inconvertible paper money to represent a claim to the huge variety of commodities available in the marketplace as well as its acceptance for the payment of debts.
Another type of money that has developed with the rise of information technology is digital currencies. The most widely known digital currency is the Bitcoin. Interestingly, Bitcoins are not issued by any central bank. They were introduced in 2009 and are created through a process called mining. That is, computer programmers create new Bitcoins by solving mathematical problems. Because the process takes time, the total supply of Bitcoins increases but only gradually. It has no physical existence or paper form. It is purely digital. It has a market value because it can be exchanged for other currencies like the U.S. dollar. Its value has plummeted at times due to low demand and a rising supply and has skyrocketed at other times due to soaring demand and a relatively slow increase in the supply. The existence of privately created monies poses serious problems for governments and central banks. Because the source of Bitcoins in transactions is more difficult to trace in comparison with paper money, they have been used for money laundering and other illegal activities. Furthermore, although Bitcoins are still a relatively new form of money and not nearly as widely used as national currencies, the expansion of its use could one day interfere with the ability of central banks to manage their nations’ money supplies. Only time will tell whether digital currencies become so widely used that they become serious competitors for national currencies.
The Neoclassical Approach to Money Supply Measurement
Before discussing how changes in the supply of money affect the economy, it is essential to discuss how it is measured. That is, it is usually helpful to address the issue of measurement before one develops a theory, remembering however that how one chooses to define and measure an economic variable may influence the theory that one develops. We saw in Chapter 1 how this problem arose when we considered how the Bureau of Labor Statistics measures the unemployment rate and the way in which that measure may influence one’s perception of a worker without a paid job. Nevertheless, one must begin somewhere, and to begin with the measurement of an economic variable seems like the easier choice.
Neoclassical economists use several primary measures of the money supply (also referred to as the money stock), and the distinction between the measures deals with the liquidity of the assets included in each measure. Liquidity refers to the ease with which an asset can be converted into currency (i.e., coins and paper money).
The first neoclassical measure of the money supply includes the most liquid assets and is referred to as the M1money supply. That is, M1 includes publicly held currency and the checkable deposits of commercial banks and thrift institutions. Thrift institutions include depository institutions like savings and loan associations and credit unions. Savings and loan associations (S&Ls) accept deposits and tend to specialize in home mortgage lending. Credit unions also accept deposits and make loans, but their members own and control them. It should be clear why M1 includes the most liquid assets. Publicly held currency is already currency and requires no conversion into currency. Note that currency held in bank vaults is not counted in the M1 money supply. Checkable deposits are also highly liquid assets. Because account holders can write checks against their balances, these deposits are easily accessed for purchases. They are also available for immediate withdrawal in the form of currency. The M1 money supply is the most closely followed measure of the money supply by the Federal Reserve, and it is the measure that is used most widely in economic models given the extreme liquidity of the assets that it includes.
The second neoclassical measure of the money supply includes less liquid assets than M1 and is referred to as the M2 money supply. The M2 money supply includes the entire M1 money supply but also includes additional assets that are less easily converted into currency. That is, M2 includes savings deposits, small time deposits (e.g., certificates of deposit valued at less than $100,000), money market deposit accounts (MMDAs), and money market mutual funds (MMMFs).
Savings deposits are held at banks and thrift institutions, but they are less liquid assets than checkable deposits because the check writing feature is absent. In addition, federal law limits the number of withdrawals per month to six. The funds can still be accessed but not quite as easily as the funds in checking accounts. Certificates of deposit (CDs) are also less liquid. These financial instruments allow the account owner to deposit a sum of money for a given period to earn a higher interest rate than what can typically be earned on a savings deposit. To earn this higher interest rate, however, the CD owner must commit the funds for a specific period. If the owner withdraws the funds before the maturity date of the CD, then a penalty must be paid. The threat of a penalty and the commitment of the funds for a specific period make this asset less liquid than a checkable deposit or even a savings deposit. Money market mutual funds and money market deposit accounts appeared in the 1970s and 1980s. Mutual fund companies offer MMMFs to investors who pool their assets together in these funds. The funds are then used to purchase money market instruments, as described in Chapter 15. MMMFs invest in highly liquid short-term assets and so are liquid as well. Investors value them for their low risk, high liquidity, and return that exceeds what can typically be earned on a savings deposit. MMDAs are like MMMFs in that the deposited funds are invested in money market instruments. Banks offer MMDAs, however, and the check writing option is limited, making them less liquid than checkable deposits.
The third neoclassical measure of the money supply is M3. The M3 money supply includes M2 but also large time deposits (i.e., CDs with values at least as great as $100,000). These CDs are so large that only institutional investors, like hedge funds and investment firms, can afford them. Because these assets are less liquid due to their longer terms to maturity and considerable penalties for early withdrawal, they are less liquid assets than the components of M2. Overall, the three neoclassical measures of the money supply tend to move together over time, although not always. The divergences between the three measures of the money supply can create a problem for the Federal Reserve as it aims to regulate the money supply.
The diagram in Figure 16.1 helps us to understand the relationship between the three neoclassical measures of the money supply.

As we move from the M1 money supply to the outer circles, we begin to include less liquid assets and so arrive at the M2 and M3 measures of the money supply. Table 16.1 provides Federal Reserve data on the M1 and M2 money stock measures as of December 2017 so that we can obtain a sense of the magnitudes of the different components of the money supply. We exclude the M3 money supply because the Federal Reserve ceased publication of it on March 23, 2006.[6]
 As Table 16.1 shows, the M1 money supply is relatively small at $3,614.3 billion (or approximately $3.6 trillion) in comparison with the M2 money supply of $13,845 billion, mainly due to the magnitude of the savings deposits. We can also see that currency and checkable deposits make significant contributions to the M1 money supply, but checkable deposits constitute a somewhat larger share of the total.
As Table 16.1 shows, the M1 money supply is relatively small at $3,614.3 billion (or approximately $3.6 trillion) in comparison with the M2 money supply of $13,845 billion, mainly due to the magnitude of the savings deposits. We can also see that currency and checkable deposits make significant contributions to the M1 money supply, but checkable deposits constitute a somewhat larger share of the total.
The most obvious example of a divergence in the growth rates of the M1 and M2 money supplies occurred in the mid-1990s. The M1 money stock contracted during this period as reflected in the negative growth rate of M1. At the same time, the growth rate of M2 was positive and rising, indicating that the M2 monetary aggregate was expanding and that the rate of expansion was increasing. The reason for this divergence may relate to the information technology revolution, which made it possible to more easily transfer funds between checkable deposits and non-M1 components of M2 such as savings deposits and money market funds. A similar reduction in the growth rate of M1 while the growth rate of M2 rose occurred in the mid-2000s before the Great Recession. One possibility is that people hold less M1 money during economic booms as they think more about profitable investment strategies. During economic contractions (the shaded areas), on the other hand, M1 money balances appear to increase as people seek security in highly liquid assets.
The Austrian Approach to Money Supply Measurement
Austrian economists agree with some aspects of the neoclassical approach to money supply measurement, but they differ sharply on several key points. Austrian economist Murray Rothbard has written extensively on this subject, and his perspective forms the basis of the Austrian approach described in this section.
First, Austrian economists strongly reject the notion that the liquidity of an asset should determine whether it is considered a part of the money supply. According to Rothbard, “the money supply should be defined as all entities which are redeemable on demand in standard cash at a fixed rate.”[7] Obviously this definition includes currency held by the public. It also includes demand deposits. Even though banks generally do not have sufficient cash reserves to redeem all outstanding demand deposits, Austrian economists emphasize the central role of subjective estimates of value by market participants. Therefore, if individuals believe that demand deposits are redeemable, they represent an active part of the money supply.[8] Austrian economists regard savings deposits held at commercial banks and savings and loan associations to be part of the money supply as well. Although some restrictions on transactions apply, depositors subjectively treat their savings deposits as redeemable for cash at a fixed rate and hence, they should be treated as part of the supply of money.[9]
Time deposits (CDs), however, are treated rather differently in the Austrian definition of the money supply. Rothbard draws upon the theory of money and credit that Ludwig von Mises developed to make this argument. Whereas a demand deposit represents a claim to cash and can be used in the purchase of present goods, a time deposit represents a credit instrument and can only be used for the purchase of future goods.[10] One cannot argue that time deposits are highly liquid assets and so should be counted as part of the money supply. Such assets are sold at market rates and are not directly redeemable for cash.[11] On the other hand, CDs and federal savings bonds are redeemable at fixed, penalty rates. Therefore, Austrian economists believe that we should include these values at their penalty levels as opposed to their face values (e.g., $9,000 as opposed to $10,000 when early withdrawal occurs).[12]
Three other issues must be discussed before providing the complete Austrian definition of the money supply. First, consistent with the Austrian criteria, the cash surrender values of life insurance policies must be included in the money supply because such policies are redeemable in cash. It is necessary, however, to add the total policy reserves minus the policy loans outstanding because the policy loans are not available for immediate withdrawal.[13] Second, if noncommercial banking institutions, such as life insurance companies or savings and loan associations, have deposits that act as reserves supporting their own issued deposits, then to avoid double counting, those reserves must be subtracted from the total demand deposits when calculating the money supply.[14] Finally, it is essential to include U.S. Treasury deposits held at the Federal Reserve in the money supply because such deposits may be used for the purchase of present goods.[15]
We can now state the complete Austrian definition of the money supply (Ma), which contrasts with the neoclassical definitions of the money supply (M1, M2, and M3).
Ma[16] = the total supply of cash
-cash held in the banks
+total demand deposits (including Treasury deposits)
+total savings deposits in commercial and savings banks
+total shares in savings and loan associations (which function like savings deposits)
+time deposits and small CDs at current redemption rates
+total policy reserves of life insurance companies
-policy loans outstanding
-demand deposits owned by savings banks, savings and loan associations, and life insurance companies
+savings bonds, at current rates of redemption
The first three items in the formula, relating to currency and demand deposits, resemble the components of M1. Savings deposits and shares closely resemble the non-M1 elements of M2. It is in the treatment of time deposits, cash surrender values, demand deposits of thrift institutions, and federal savings bonds where we see the greatest difference between the Austrian definition of the money supply and the neoclassical definitions of the money supply. The major reason for the differences in the definitions is that neoclassical economists concentrate on the liquidity of the assets in their definitions whereas Austrian economists focus on the potential to redeem the assets for cash at fixed rates even if the redemption rates are penalty rates.
The Origin of Fractional Reserve Banking
Now that we understand the most important measures of the money supply, we will begin thinking about how the money supply is determined within capitalist economies. We thus move from the practical problem of measurement to the theoretical problem of determination. To address the problem of money supply determination, we will consider two contrasting theories of the way in which a private commercial banking system helps determine the M1 money supply. Because the central bank also plays a major role in determining the M1 money supply, the neoclassical and Marxist theories of money supply determination that we develop in this chapter are only partial theories. The role that the central bank plays in determining the money supply is the subject of Chapter 17.
To understand the contribution of private commercial banks to the determination of the M1 money supply in neoclassical theory and in Marxist theory, we need to first distinguish between 100% reserve banking systems and fractional reserve banking systems. To make sense of this distinction, it is helpful to imagine an economy with a money commodity like gold.[17] Suppose that owners of gold bars decide that it is a great burden to use gold bars each time they wish to buy commodities. Some enterprising young person sees this problem as an opportunity to earn an income. Suppose that she offers to safeguard the gold bars for their owners (for a fee) and offers to issue paper certificates in an amount that is equivalent to the gold bars. These paper certificates are payable in gold on demand. The entire money supply now consists of the total supply of paper certificates, plus any gold bars that remain in circulation. Although a money commodity may still circulate, convertible paper money is now the dominant type of money in this economy.
This economy possesses what economists call a 100% reserve banking system. That is, 100% of the circulating paper certificates are backed up with gold reserves. If every holder of a paper certificate decided at the same time to redeem their certificates for gold, then the banker who issued the certificates would be able to satisfy every certificate owner’s demand for gold bars. The likelihood of everyone redeeming their paper certificates at once is very low, but it could happen if the holders of the certificates begin to doubt whether the banker will pay them in gold. If their faith is shaken enough, then a bank run might occur where every certificate owner demands payment in gold at the same time. It is worth noting that bank runs of this kind create no problems in a 100% reserve banking system because the demand for gold bars can be completely satisfied without delay.
If sufficient faith in the 100% reserve banking system exists, then most holders of paper certificates are very unlikely to redeem their paper notes for gold. After all, the convertible paper money was created so that owners of gold bars would not need to concern themselves with the protection of the gold bars or the burden of hauling them around to engage in market exchanges. It is the low rate of redemption of the paper certificates that causes the private banker to consider another potential source of income. She decides to create and issue new paper certificates to the point where the face value of the certificates exceeds the quantity of gold reserves that she holds. By doing so, she has expanded the convertible paper money supply and has thus created new money. Rather than using these new certificates for purchases, which she could do, the private banker decides to grant loans, in the form of paper certificates, to borrowers who agree to repay her at a future date with interest. The granting of loans has thus expanded the paper money supply. The total money supply now consists of the original certificates that were issued in exchange for deposits of gold bars, the newly issued certificates representing loans to borrowers, and any gold bars that remain in circulation. The total money supply (M) can be calculated as follows:
M = original certificates + additional certificates (representing loans) + publicly held gold bars
Because the face value of the convertible paper money supply exceeds the value of the gold reserves held in the bank, the banking system is regarded as a fractional reserve banking system. That is, the reserves held in the bank only partially support the convertible paper money that is circulating in the economy. In other words, the value of the reserves only equals a fraction of the value of the circulating paper money. Now a bank run has serious consequences for the banker. If every holder of a paper certificate decides to redeem the certificates for gold bars, then the banker will not be able to satisfy those demands. If the rule of law is not firmly established, then the banker might suffer violence at the hands of an angry mob. Figure 16.3a summarizes the results of this analysis:

From an efficiency perspective, neoclassical economists argue that it is understandable that institutions would create and issue convertible paper money. Holders of gold and silver do not want to pay for other commodities directly using these commodities because they are heavy and difficult to transport. Banking institutions arose to specialize in the safeguarding of these assets. Owners of gold and silver are willing to pay for this service and bankers aim to profit from its provision. Nevertheless, it is the granting of loans and the creation of new money that has the potential to make banking so profitable and so risky because of the constant danger of bank panics and bank runs.
Because modern economies have abandoned commodity money, you might think that this analysis is obsolete with no practical application to modern banking systems. On the contrary, this analysis is entirely applicable to modern banking systems. The only important difference is that the material that serves as bank reserves and the asset that serves as a claim to those reserves have changed.
The dominant type of money in the U.S. economy is government-issued fiat money, as described earlier in this chapter. Although paper money is easier to use in transactions than gold bars, it is still a burden to use for all transactions, particularly large transactions. Therefore, commercial banks accept currency deposits, which perfectly parallels the deposits of gold bars in our economy based on the gold standard. It would not make much sense to issue paper certificates in exchange for the currency deposits, however, because paper would then simply circulate in place of paper. Instead, banks issue checkable deposits when currency deposits are made. The checkable deposits are analogous to the paper certificates in the gold standard economy. Purchases are made using paper checks that can be written in any amount to access the underlying deposits. It is important to remember that it is the underlying checkable deposits that represent money in modern banking systems, not the paper checks that only allow one to access them. The total money supply (M1) for this economy can be calculated as follows:
M1 = original checkable deposits + additional deposits (representing loans) + publicly held currency
Just as in the case of the gold standard economy, private commercial banks recognize that they can issue checkable deposits in an amount that exceeds the reserves of U.S. dollars that they hold. It is a desire to grant interest-bearing loans that motivates the issuance of additional checkable deposits. Because checkable deposits are part of the M1 money supply, the issuance of additional checkable deposits represents the creation of new money. A 100% reserve banking system is possible in an economy based on fiat money if the banks only create checkable deposits in response to the receipt of currency deposits. As soon as the face value of the deposits exceeds the reserves of U.S. dollars held in bank vaults, the system becomes a fractional reserve banking system and is vulnerable to the threat of bank runs. Figure 16.3b summarizes the results of this analysis.
The Balance Sheet of a Commercial Bank
To investigate more carefully how commercial banks influence the total quantity of money available in the economy, it is helpful to use a financial statement known as a balance sheet. A balance sheet is a financial statement that provides a snapshot of an entity’s financial position at a point in time. Balance sheets can be constructed for individuals and for firms. The balance sheet has two columns. On the left side of the balance sheet, all the assets of the individual or firm are listed with their associated values. The assets are simply items of property that the entity owns. The right side of the balance sheet lists all the liabilities and the net worth of the entity. Liabilities and net worth represent claims against the assets. Liabilities are external claims to the assets of the entity. That is, they represent the claims of non-owners to the entity’s assets and so they are debts for the individual or firm. Net worth (also referred to as equity) represents an internal claim to the assets of the household or firm. That is, after accounting for all the debts, the net worth of the entity represents its claim to the remaining assets. When people sometimes ask how much someone is worth, they have in mind their net worth. That is, they are asking how much property a person owns after subtracting her debts. We can obtain a better understanding of the balance sheet concept if we consider a simple example of how this financial statement might look for one individual as shown in Figure 16.4.

The individual whose balance sheet is represented in Figure 16.4 possesses several different types of assets, including cash, a checkable deposit, a savings deposit, and an automobile. She also has incurred debts to obtain these assets, including an auto loan and a credit card loan. The auto and credit card loans represent liabilities because the lending agencies have claims to the individual’s assets. Because the individual’s assets exceed her liabilities, her net worth is positive, representing her claim to her own assets. Because every asset will be claimed by someone (i.e., owners or non-owners), the total assets must equal the sum of the liabilities and net worth. The balance sheet equation may thus be written as:
Assets = Liabilities + Net Worth (equity)
It should be noted that liabilities may exceed assets. When this situation arises, net worth must be negative for the balance sheet equation to hold. A negative net worth means that the individual or firm is insolvent and may need to declare bankruptcy to rectify the situation.
In this chapter, we are primarily interested in how the activities of private commercial banks influence the money supply and the financial markets. Therefore, we need to look at the balance sheet of a commercial bank. The items that typically appear on a bank’s balance sheet are different from the items that generally appear on a firm’s balance sheet or an individual’s balance sheet. Figure 16.5 shows a consolidated balance sheet for all commercial banks in the United States as of January 10, 2018.[18]

Only the most essential balance sheet items have been included in Figure 16.5. The asset side of the balance sheet includes securities, which totaled nearly $3.5 trillion in January 2018. Commercial banks purchase income-earning assets such as U.S. Treasury securities and mortgage-backed securities (MBSs). U.S. Treasury securities include short-term money market instruments such as Treasury bills that have terms to maturity of less than one year and long-term capital market instruments such as Treasury notes and Treasury bonds that have terms to maturity of greater than one year. Mortgage-backed securities are assets that represent bundles of many mortgage loans with varying degrees of risk that generate interest income for the owner over time. MBSs were created rapidly during the leadup to the 2008 financial crisis and banks continue to hold large quantities of these assets.
Loans are another important asset on the consolidated balance sheet of U.S. commercial banks. In fact, loan assets are the largest item on the balance sheets of banks at over $9.1 trillion in January 2018. This fact should not surprise the reader. After all, fractional reserve banking developed precisely because banks discovered that they could earn interest income by granting loans to borrowers. This category includes loans of all kinds, including commercial loans, industrial loans, real estate loans, and consumer loans. It is the most profitable activity in which banks engage, but it is also the riskiest activity because borrowers sometimes default (or fail to repay) their loans with interest. When such defaults occur, banks experience loan losses, which accounts for the $110 billion asset reduction in Figure 16.5. During the Great Recession, a wave of defaults on residential mortgages occurred, which caused the values of MBSs to collapse and wiped out a massive amount of wealth that only existed on paper. If such loan losses are large enough, then it might cause assets to fall below liabilities, causing insolvency.
The final item of importance on the asset side of commercial banks’ balance sheets is cash reserves. Cash reserves include currency that is held in bank vaults, which is not part of M1. It also includes funds that are held in accounts with the Federal Reserve. Cash reserves are important because they make it possible for banks to satisfy depositors’ demands for cash withdrawals or withdraws that occur by means of writing checks. Within a fractional reserve banking system, these cash reserves are generally a fraction of the total deposit liabilities. In this case, cash reserves are approximately 20.11% of total deposit liabilities (= 2,405.4/11,960.2) so that for each dollar of deposits, the bank maintains about $0.20 in cash reserves.
On the liabilities and net worth side of the balance sheet, the main categories include deposits and borrowings. Deposits are the largest category of liabilities at nearly $12 trillion in January 2018. Deposits are created when depositors transfer funds to banks, either by means of cash deposits or check writing. Because depositors do not own the bank, their claims to the assets of banks are external claims or liabilities. This category of liabilities includes checkable deposits but also savings deposits and time deposits.
The other major category of liabilities for banks is borrowings at just over $2 trillion. Borrowings include funds borrowed from other commercial banks, the Federal Reserve, and corporations. When commercial banks borrow from other commercial banks, they do so in the federal funds market. The federal funds market is the market for overnight loans made between banks when they lend their reserves to one another. The interest rate that emerges in this market due to the competitive interaction between borrowing banks and lending banks is the federal funds rate. This interest rate fluctuates with changes in the supply and demand for reserves. Another type of borrowing is borrowing from the Federal Reserve. Loans that the Federal Reserve grants to commercial banks are called discount loans. The Fed charges an interest rate on such loans that is referred to as the discount rate. Finally, banks also borrow from corporations. Banks sell large certificates of deposit to corporations in exchange for the use of funds for a fixed period. In exchange for this privilege, banks pay high rates of interest to the lenders.
The final item of importance on the banks’ balance sheet is what we have previously called net worth or equity. The owners of the banks possess a claim to the assets of banks. In this case, the owners are the stockholders, and so net worth is sometimes referred to as stockholders’ equity. In the special case of banking institutions, net worth is also referred to as bank capital. Because the phrase is so widely used, when we refer to the net worth of banks, we will refer to bank capital. In January 2018, total bank capital for U.S. commercial banks approached $1.9 trillion. Adding together the items on each side of the balance sheet yields approximately $16.74 trillion of assets and $16.74 trillion of liabilities plus bank capital. As expected, the two sides of the balance sheet add up to the same total. Although we have considered the consolidated balance sheet of all U.S. commercial banks, each commercial bank has its own balance sheet. The balance sheet equation holds for each bank’s balance sheet, and each item on the consolidated balance sheet is simply the total for that item across all individual banks’ balance sheets.
A Neoclassical Theory of Commercial Banks and its Theory of Financial Markets
This section explores the way in which neoclassical economists interpret commercial bank behavior and how banks influence the total stock of money. The neoclassical analysis that we develop is also linked to the neoclassical theory of financial markets presented in Chapter 15. That is, it will be shown how neoclassical theory provides an explanation for movements in bond prices and interest rates.
The reader should keep in mind that commercial banks are profit-seeking institutions just like production firms. They do not aim to alter the supply of money but do so when seeking maximum profits. To maximize profits, banks must undertake a delicate balancing act that involves carefully adjusting the various items on their balance sheets. Indeed, the profits of a bank depend on the selected mix of the different conflicting balance sheet items.
The management of banks involves different and often competing objectives.[19] For example, banks must purchase assets that will generate maximum income for the bank. Loan assets are the greatest generator of bank income, but securities are also an important source of income for banks. At the same time, banks must also acquire funds at minimum cost to the bank. Because liabilities include deposits of all kinds, banks must pay interest to acquire and maintain them. Even in the case of checkable deposits that pay no interest at all, commercial banks compete for new depositors and frequently offer cash bonuses to depositors who open new checking accounts. Banks also need to acquire and maintain sufficiently liquid assets so that the banks can satisfy depositors’ demands for withdrawals. Cash reserves are the most liquid bank asset. Short-term securities, such as Treasury bills, are also relatively liquid assets and can be converted into currency at relatively low cost. Finally, banks are required to maintain sufficient levels of bank capital so that if loan losses occur, the banks will not become insolvent. Since liabilities are fixed, when loan losses occur, net worth or bank capital must shrink to maintain overall balance on the balance sheet. If bank capital falls to the point where it becomes negative, then the bank is technically insolvent.
The way that private commercial banks strategize to achieve maximum profits is a subject of great interest, but we set it aside in this chapter to concentrate on the influence that banks and private individuals have on the major measures of the money supply. In other words, we are interested in the reasons for shifts in the money supply curve that occur in the money market as described in Chapter 15. Figure 16.6 shows how the M1 money supply may increase to M1* or decrease to M1** in the money market.
 To explore the role of banks in changing the money supply, we only show the changes that occur to the balance sheet items and exclude all items that remain unaffected when a transaction occurs. This approach greatly simplifies the presentation and allows us to focus on the consequences of interactions between commercial banks and other entities. The impact on the monetary aggregates should also be clearer.
To explore the role of banks in changing the money supply, we only show the changes that occur to the balance sheet items and exclude all items that remain unaffected when a transaction occurs. This approach greatly simplifies the presentation and allows us to focus on the consequences of interactions between commercial banks and other entities. The impact on the monetary aggregates should also be clearer.
When a $500 cash deposit occurs, the bank acquires $500 in cash reserves and $500 in deposit liabilities. The transaction has no impact on the M1 money supply. Although checkable deposits increase, publicly held currency falls by an equal amount. The overall result is an unchanged M1 money supply. M2 is similarly unaffected because M2 includes M1. With M1 remaining the same, M2 remains the same as well.
Now consider a cash withdrawal of $500. This transaction also has no impact on the M1 or M2 money supplies. When the withdrawal occurs, deposit liabilities fall by the same amount as publicly held currency rises. M1 and M2 are thus unchanged in this case. Figure 16.7 (b) shows the changes to the balance sheet that occur when a $500 cash withdrawal occurs.
Similar changes to the balance sheet occur when these transactions are carried out by check rather than with currency. For example, when an account holder deposits a $500 check in Bank A, the check is sent to the Federal Reserve Bank in that district. The Fed then credits the account of Bank A, thus increasing its reserves. Deposit liabilities also increase for Bank A. The only difference is that a cash deposit has an immediate impact on vault cash, whereas the deposit of a check has a quick, although not immediate, impact on the bank’s reserves held at the Fed. The impact is not immediate because the check must be processed and must clear before the bank’s reserves increase in the case of a check being deposited.
If the check was written against an account at Bank B, then Bank B experiences a loss of reserves when the Fed adjusts the reserves. Bank B also experiences a reduction in its deposit liabilities. Because deposits at Bank A increase and deposits at Bank B decrease, the total M1 and M2 money supplies remain the same.
Figure 16.8 shows the impact on the Federal Reserve’s balance sheet.
 Figure 16.8 shows how the Fed’s balance sheet adjusts due to the processing of the check. The changes illustrate a couple important points. First, the reserves that banks hold in their accounts with the Fed are treated as liabilities of the Fed even though they are assets for the banks. The Fed owes the banks these funds, and they represent external claims to the Fed’s assets. Second, balance sheet changes need not affect both sides of a balance sheet. That is, an increase in one category of liabilities may be offset by a reduction in another category of liabilities. The Fed’s total liabilities do not change, but these changes make it possible to increase the reserves of Bank A and to reduce the reserves of Bank B. Those changes cause the deposit liabilities of Bank A to increase and the deposit liabilities of bank B to decrease. Because the total checkable deposit liabilities in the banking system remain the same, the M1 and M2 money supplies remain unchanged.
Figure 16.8 shows how the Fed’s balance sheet adjusts due to the processing of the check. The changes illustrate a couple important points. First, the reserves that banks hold in their accounts with the Fed are treated as liabilities of the Fed even though they are assets for the banks. The Fed owes the banks these funds, and they represent external claims to the Fed’s assets. Second, balance sheet changes need not affect both sides of a balance sheet. That is, an increase in one category of liabilities may be offset by a reduction in another category of liabilities. The Fed’s total liabilities do not change, but these changes make it possible to increase the reserves of Bank A and to reduce the reserves of Bank B. Those changes cause the deposit liabilities of Bank A to increase and the deposit liabilities of bank B to decrease. Because the total checkable deposit liabilities in the banking system remain the same, the M1 and M2 money supplies remain unchanged. The cash deposit causes savings deposit liabilities to increase and publicly held currency to fall. Because publicly held currency falls with no change in checkable deposits, the result is a decrease in the M1 money supply. The M2 money supply remains unaffected, however, because savings deposits are included in M2, as is publicly held currency. In other words, the rise in savings deposits exactly offsets the decline in publicly held currency in M2.
The cash deposit causes savings deposit liabilities to increase and publicly held currency to fall. Because publicly held currency falls with no change in checkable deposits, the result is a decrease in the M1 money supply. The M2 money supply remains unaffected, however, because savings deposits are included in M2, as is publicly held currency. In other words, the rise in savings deposits exactly offsets the decline in publicly held currency in M2.
Figure 16.9 (b) shows the impact of a cash withdrawal of $500 from a savings account on the bank’s balance sheet.
A deposit of a $500 check drawn against a checkable deposit at one bank into a savings account at another bank would also decrease the M1 money supply. In that case, checkable deposits at one bank would fall and savings deposits at another bank would rise. M1 would fall and M2 would remain the same.
The Fed would adjust the reserves of the two banks, as shown in Figure 16.8, but the impact on the M1 and M2 money supplies is the same as what we observe in the case of a cash deposit in a savings account.
One other transaction worth considering is a transfer between accounts. If an individual owns a checkable deposit and a savings deposit and decides to transfer $500 worth of funds from her checking account to her savings account, then the M1 money supply falls by $500 and the M2 money supply remains the same.
Again, checkable deposits are included in M1 but not in M2. The resulting change to the bank’s balance sheet due to this transfer is shown in Figure 16.10 (a). Similarly, a transfer of $500 from a savings account to a checking account increases the M1 money supply by $500 and leaves M2 unchanged.
The impact of a transfer from a savings deposit to a checkable deposit on a bank’s balance sheet is shown in Figure 16.10 (b).

This section has analyzed the impact on M1 of movements of funds between publicly held currency or checkable deposits, and savings deposits. The same results apply to similar movements of funds between publicly held currency or checkable deposits into and out of other non-M1 aspects of M2, including MMDAs, MMMFs, and time deposits.
Members of the public can certainly have an impact on the M1 money supply when they make deposits into M1 from savings accounts and the other non-M1 aspects of M2. Withdrawals from M1 into savings accounts and the other non-M1 aspects of M2 also influence M1. The more important source of changes in the M1 money supply, however, include activities that banks initiate. For example, when loans are granted or are repaid, they have a direct impact on the M1 and M2 money supplies.
First consider what happens when a commercial bank grants a $3,000 loan to a borrower. The borrower signs a loan contract or a promissory note, agreeing to repay the loan within a specified period with regular interest payments. The bank accepts the promissory note, which is a non-money asset and credits the checking account of the borrower, which is an M1 money asset. The impact of the transaction on the balance sheet of the bank is represented in Figure 16.11.
 The bank has acquired a loan asset and has created a checkable deposit. It should be noted that the bank has no additional cash reserves and so publicly held currency did not change. The deposit was created using a non-money asset. The bank has created new money! Both the M1 and M2 money supplies increase due to the loan.
The bank has acquired a loan asset and has created a checkable deposit. It should be noted that the bank has no additional cash reserves and so publicly held currency did not change. The deposit was created using a non-money asset. The bank has created new money! Both the M1 and M2 money supplies increase due to the loan.
The creation of new money with the issue of additional checkable deposits parallels the issue of new paper certificates in the gold standard economy we considered earlier in this chapter. The bank sees an opportunity to make a profit and takes advantage of the fact that most deposits will not be withdrawn during the period of the loan. The borrower’s deposit is likely to be quickly withdrawn, however, because the borrower has incurred considerable expense to obtain the funds and plans to use them. Whether it is withdrawn in the form of currency or due to the Fed’s check processing activities, the M1 money supply is not expected to be directly affected due to the withdrawal. It is the granting of the initial loan, however, that has created new money.
The bank incurs some risk when it creates new money because the more money it creates, the more likely it is that it will not have sufficient reserves to satisfy depositors who write checks against their balances or who make cash withdrawals. Therefore, the Federal Reserve imposes a reserve requirement, which is a legal requirement that banks maintain a minimum fraction of their deposit liabilities as reserves, which is stated as a percentage of the bank’s deposit liabilities. Banks may also choose to hold excess reserves above the reserve requirement. To understand how reserve requirements work, consider the balance sheet of the bank shown in Figure 16.12.
 The bank is subject to a 10% legal reserve requirement. It has cash reserves of $12,000 and deposit liabilities of $100,000. Clearly, the banking system is a fractional reserve banking system since not all deposits are supported with fiat money reserves. Nevertheless, this bank is meeting its reserve requirement since the ratio of currency to deposits (C/D) is equal to 12%. In fact, the bank is exceeding the minimum requirement and has excess reserves of $2,000, which could be used to legally expand the money supply through lending.
The bank is subject to a 10% legal reserve requirement. It has cash reserves of $12,000 and deposit liabilities of $100,000. Clearly, the banking system is a fractional reserve banking system since not all deposits are supported with fiat money reserves. Nevertheless, this bank is meeting its reserve requirement since the ratio of currency to deposits (C/D) is equal to 12%. In fact, the bank is exceeding the minimum requirement and has excess reserves of $2,000, which could be used to legally expand the money supply through lending.
Figure 16.3a shows that the bank’s deposit liabilities decline by $3,000, but its reserves also decrease by $3,000. The borrower has either withdrawn the funds in the form of currency or has written a check against the amount. During the period of the loan, the loan asset increases in value due to the anticipation of a final payment of interest when the loan matures. If the interest rate (i) is 5%, then the loan asset appreciates by $150 (=5% times $3,000). Because the bank’s deposit liabilities have not changed, the bank’s shareholders enjoy an increase in bank capital. This change is represented in Figure 16.3b.

When the loan matures, the borrower must repay the principal amount plus interest. She, therefore, deposits the full amount of $3,150 in her account at the bank. The bank’s deposit liabilities rise by this amount. The bank’s reserves also increase by this amount giving balance to the balance sheet. This change is shown in Figure 16.3c.

Finally, the borrower repays the loan with a check drawn against her account at the bank. The bank debits the borrower’s account, which reduces the bank’s deposit liabilities. It also returns the canceled promissory note to the borrower as shown in Figure 16.13d.

Notice that the bank has $3,150 in reserves, which is $150 more than the amount with which it began. It also has increased its bank capital by $150, which reveals how interest-bearing loans serve as a means of appropriating profits for the bank and enhancing bank capital. Most importantly, we see that when loans are repaid, the M1 and M2 money supplies contract. Borrowers repay loans with interest. They receive the canceled promissory notes, and their checking accounts are debited. A non-money asset returns to circulation, and a money asset leaves circulation.
It is assumed that the borrower redeposited the initial loan amount and made an additional cash deposit of $150 to make possible the repayment of interest with the loan. When these cash deposits are made, the M1 and M2 money supplies do not change because publicly held currency falls as much as checkable deposits increase. It is only when the loan is repaid that the M1 money supply falls by the full amount of the repayment. Interest payments on bank loans thus contribute to the contraction of the money supply.
In Figure 16.13d, the M1 and M2 money supplies fall because checkable deposits decline with no change in publicly held currency.
It is the canceled promissory note that returns to the borrower, not currency, as would occur in the case of a cash withdrawal. Hence, both monetary aggregates contract. It is worth noting that banks can change both M1 and M2 with their lending activities whereas deposits and withdrawals from savings accounts (and other non-M1 components of M2) only affect M1.
Another operation of commercial banks that has similar impacts on the M1 and M2 money supplies is the purchase and sale of government securities. In this case, government securities act in the role of non-money assets like promissory notes. Otherwise, the process is essentially the same. Banks purchase government securities from bond dealers and credit their checking accounts to pay them, which expands the M1 and M2 money supplies. When banks sell government securities to bond dealers, the dealers pay using their checkable deposits, and the M1 and M2 money supplies contract. Non-money assets return to circulation, and money assets are taken out of circulation.
We can now see exactly how the financial markets are affected due to the different operations we have been discussing. The previous discussion has shown that the M1 money supply can be increased due to the following bank operations:
- A cash withdrawal from a savings account (or other non-M1 M2 asset account)
- A transfer from a savings account (or other non-M1 M2 asset account) to a checking account
- A loan granted to a borrower
- A purchase of government securities from a bond dealer who is paid with cash or with a check that is then deposited in a checking account
If any of these transactions takes place, the resulting increase in the M1 money supply will have a direct impact on the financial markets. Figure 16.14 shows how the monetary expansion connects with our theory of financial markets developed in Chapter 15.

As Figure 16.14 shows, when the M1 money supply rises, the money supply curve shifts rightward in the money market. At the initial interest rate, a surplus of money exists. Because holders of money hold excess money balances, they decide to lend it in the loanable funds market to earn interest. The rightward shift of the supply curve for loanable funds creates a surplus of loanable funds. Competition between borrowers and lenders in the loanable funds market drives down the rate of interest, which clears the money market. At the same time, the rise in the supply of loanable funds is equivalent to an increase in the demand for bonds since these two markets represent a mirror reflection of one another. The higher demand for bonds pushes bond prices upward. Overall, the monetary expansion leads to an expansion of the loanable funds market and the bond market. Interest rates drop, and bond prices rise.
Similarly, the M1 money supply will decline due to the opposite bank operations:
- A cash deposit into a savings account (or other non-M1 M2 asset account)
- A deposit of a check drawn against a checking account into a savings account (or other non-M1 M2 asset account)
- A transfer from a checking account into a savings account (or other non-M1 M2 asset account)
- A loan repayment
- A sale of securities to a bond dealer who pays with cash or check drawn against a checking account
If any of these transactions takes place, the resulting decrease in the M1 money supply will have a direct impact on the financial markets. Figure 16.15 shows how the monetary contraction connects with our theory of financial markets developed in Chapter 15.

As Figure 16.15 shows, when the M1 money supply falls, the money supply curve shifts leftward in the money market. At the initial interest rate, a shortage of money exists. Because holders of money experience a shortage of money balances, they decide to lend fewer funds in the loanable funds market. The leftward shift of the supply curve for loanable funds creates a shortage of loanable funds. Competition between borrowers and lenders in the loanable funds market drives up the rate of interest, which clears the money market. At the same time, the reduction in the supply of loanable funds is equivalent to a reduction in the demand for bonds since these two markets represent a mirror reflection of one another. The drop in the demand for bonds pushes bond prices downward. Overall, the monetary contraction leads to a contraction of the loanable funds market and the bond market. Interest rates rise, and bond prices fall.[20]
One other aspect of the neoclassical theory of banking that is important is the multiple expansion of bank deposits through lending. That is, when First Regional Bank obtains new reserves and makes a loan, the new checkable deposit that is created adds to the M1 money supply. The process does not stop there, however, because the recipient of the check that is written against those funds (i.e., whomever the borrower of the funds decides to pay to obtain commodities) is likely to deposit the check in a Second Regional Bank checking account. Second Regional Bank will acquire new reserves. If Second Regional Bank lends the excess reserves, then another new checkable deposit is created. A check is then written against those funds and the recipient of the check might deposit the check in Third Regional Bank. Third Regional Bank thus receives new reserves and might lend the excess reserves, thereby creating yet another new checkable deposit. This process continues and each time a new checkable deposit (i.e., new money) is created. This process is referred to as the multiple expansion of bank deposits.
To understand the exact quantitative relationship between new reserves in the banking system and the amount of new checkable deposits or new money that is created, we need to look at the impact of these successive rounds of lending on the banks’ balance sheets. Consider the changes to First Regional Bank’s balance sheet when the bank accepts a $2,000 cash deposit and obtains $2,000 in new reserves. Assume that it is also subject to a 10% reserve requirement and so grants a $1,800 loan using the new excess reserves and that the borrower withdraws the entire amount from his checking account once the loan is granted. All these changes are depicted in Figure 16.16.
 In Figure 16.16, the deposit is made, and the bank acquires new reserves. It then grants a loan, acquiring a loan asset and creating a checkable deposit. Finally, the borrowed amount is withdrawn from the checking account, and the reserves decline by an equal amount. The reader should verify that the net effect is a $2,000 increase in bank assets and a $2,000 increase in liabilities. The M1 money supply has risen by $1,800 due to the granting of the loan.
In Figure 16.16, the deposit is made, and the bank acquires new reserves. It then grants a loan, acquiring a loan asset and creating a checkable deposit. Finally, the borrowed amount is withdrawn from the checking account, and the reserves decline by an equal amount. The reader should verify that the net effect is a $2,000 increase in bank assets and a $2,000 increase in liabilities. The M1 money supply has risen by $1,800 due to the granting of the loan. The M1 money supply rises by $1,620 due to Second Regional Bank granting the loan and creating the new deposit. Let’s finally consider how Third Regional Bank’s balance sheet is affected if the $1,620 of borrowed funds is deposited there. Again, Third Regional Bank will acquire new reserves equal to $1,620. It will lend 90% of the newly acquired reserves (i.e., the excess reserves). The $162 of required reserves must be kept in the form of cash reserves. Second Regional Bank will lend $1,458 to a borrower and create a new checkable deposit, which adds to the M1 money supply. It will then be withdrawn, and the process continues. The changes to Third Regional Bank’s balance sheet are shown in Figure 16.18.
The M1 money supply rises by $1,620 due to Second Regional Bank granting the loan and creating the new deposit. Let’s finally consider how Third Regional Bank’s balance sheet is affected if the $1,620 of borrowed funds is deposited there. Again, Third Regional Bank will acquire new reserves equal to $1,620. It will lend 90% of the newly acquired reserves (i.e., the excess reserves). The $162 of required reserves must be kept in the form of cash reserves. Second Regional Bank will lend $1,458 to a borrower and create a new checkable deposit, which adds to the M1 money supply. It will then be withdrawn, and the process continues. The changes to Third Regional Bank’s balance sheet are shown in Figure 16.18.
 We could explore the roles of Fourth Regional Bank, Fifth Regional Bank, and Sixth Regional Bank, and on and on, but the pattern should be clear by now.
We could explore the roles of Fourth Regional Bank, Fifth Regional Bank, and Sixth Regional Bank, and on and on, but the pattern should be clear by now.
The M1 money supply increases with each successive round of lending and deposit creation. With each round of lending, however, the new loan amounts become smaller and smaller. The reason for the reduction in deposit creation is that banks must hold a fraction of their newly acquired reserves each time they receive the deposited funds. The legal reserve requirement limits the banks to the creation of new money equal only to their excess reserves. As the story continues, the newly created deposits become smaller and smaller until they cease to influence the M1 money supply.
To arrive at an exact calculation of the total new checkable deposits that are created due to the acquisition of new reserves in the first round, we consider a situation in which First Regional Bank acquires only $1.00 of new reserves. If R is the reserve requirement (10% in our example), then R (= 0.10) represents the required reserves in this case (i.e., 10 cents or $0.10). The excess reserves that First Regional Bank acquires are 1-R (= 90 cents or $0.90). The loan amount or newly created checkable deposit is assumed to equal the full amount of the excess reserves and so is also equal to 1-R. The first row of Table 16.2 shows the results for First Regional Bank.

Second Regional Bank then acquires the 1-R amount of borrowed funds, which for it constitute new reserves. Its new required reserves are R times this amount or R(1-R). The excess reserves are 1-R times this amount or (1-R)(1-R) = (1-R)2. The excess reserves are then loaned to a borrower and a new deposit is created in the amount of (1-R)2. The second row in Table 16.2 captures these results.
Third Regional Bank then acquires the borrowed amount of (1-R)2 in the form of reserves. Its required reserves are R times this amount or R(1-R)2 and its excess reserves are 1-R times the new reserves or (1-R)(1-R)2 = (1-R)3, which is then loaned to a borrower. The third row in Table 16.2 captures these results. The results for Fourth Regional Bank have also been added to the table. Readers should think through those results to test their understanding.
To determine the total amount of new deposits created, we need to add up all the entries in the last column, which represents new money created. The change in deposits (D) can be represented as follows:
We can then factor out (1-R), which makes it possible to solve for D as follows:
This important result allows us to obtain an exact quantitative solution to the problem of the amount of deposits that can be created using the newly acquired reserves at the First Regional Bank. In that example, the reserve requirement is 10% and so the simple deposit multiplier is simply the reciprocal of the reserve requirement or 1/0.10 = 10. The newly acquired excess reserves at the First Regional Bank are equal to $1,800. Although this bank can only create $1,800 of new money using these excess reserves, the entire banking system can create ten times this amount, or $18,000. The M1 money supply thus rises by $18,000 once the money multiplier process has run its course. In general, when a loan is granted, the M1 money supply curve shifts rightward in the money market, but it may shift by an amount that is much larger than the initial loan amount due to the multiple expansion of bank deposits.
Two factors may weaken the money multiplier process. First, banks frequently choose to hold excess reserves to maintain liquid positions. Because these reserves exceed the minimum legal requirement, they reduce the impact of the money multiplier. If banks hold more reserves, then fewer funds are loaned out, and fewer new deposits are created. Second, if borrowers choose to hold some of their borrowed funds in the form of currency (or the recipients of those borrowed funds when the borrowers pay them for commodities), then the money multiplier process weakens. Currency that is held and not redeposited in the banking system does not add to the reserves of banks and cannot be loaned or used to create new deposits. Because the tendencies of banks to hold excess reserves or the public to hold currency are very real, the money multiplier that we developed in this section is almost certainly larger than we would observe. Advanced money and banking textbooks develop a more complex money multiplier that considers the existence of excess reserves and the currency leakages that occur when the borrowing public decides to hold cash.
Clearly the activities of banks and depositors have a major influence on the M1 money supply. At the same time, neither banks nor the depositors act with the intention of influencing the M1 money supply. According to neoclassical economics, banks are profit-seeking organizations and make decisions about loans and purchases and sales of securities without regard to the impact on the total stock of money in the economy. Similarly, depositors are utility-maximizing consumers and savers and make their decisions about the amount of money to hold without any concern for how their decisions might alter the money supply. Since the state of the economy can sometimes causes banks and depositors to act in predictable ways, the M1 money supply might be subject to extreme fluctuations. For example, during an economic downturn, banks restrict their lending, which reduces the M1 money supply and may intensify a recession. During an economic upswing, banks expand their lending, which might sharply increase the M1 money supply and may cause inflation. Similarly, if depositors decide to hold more currency during a recession, then banks will have fewer reserves to lend, which can worsen a recession. If they decide to deposit more currency in savings deposits (and other non-M1 M2 assets) during an economic expansion, then banks will have more reserves and are likely to grant more loans, which will expand the M1 money supply overall through the multiple expansion of checkable deposits. The potential impact on the M1 money supply stemming from the activities of banks and the public raises the question as to whether the determination of M1 should be left to the private banking community. The history of bank panics and bank runs in the United States provides part of the justification for the establishment of a central bank to regulate the money supply. The role of the central bank in money supply regulation is the subject of Chapter 17.
A Marxist Theory of Commercial Banks and its Theory of Financial Markets [21]
The major difference between the neoclassical and Marxist theories of commercial banking and financial markets that we explore in this chapter is that Marxists assign a central role to class conflict in their analyses of commercial bank behavior and financial markets. The Marxist theory developed in this section is not one that Marx created, but the concepts that Marx shaped directly inspired it. We begin with a reminder about the general formula for capital that is discussed in Chapter 4. Symbolically, capital takes the form of money and commodities but becomes capital when it participates in the following movement:
According to this symbolic representation, M’ is equal to M+ΔM where M represents surplus value. The capitalist thus transforms a sum of money capital (M) into more money (M’). This circuit of money capital may be expanded, as described in Chapter 4, to show that the money capital is advanced for the purchase of labor-power (Lp) and means of production (mop). Figure 16.19 shows the expanded circuit of money capital.
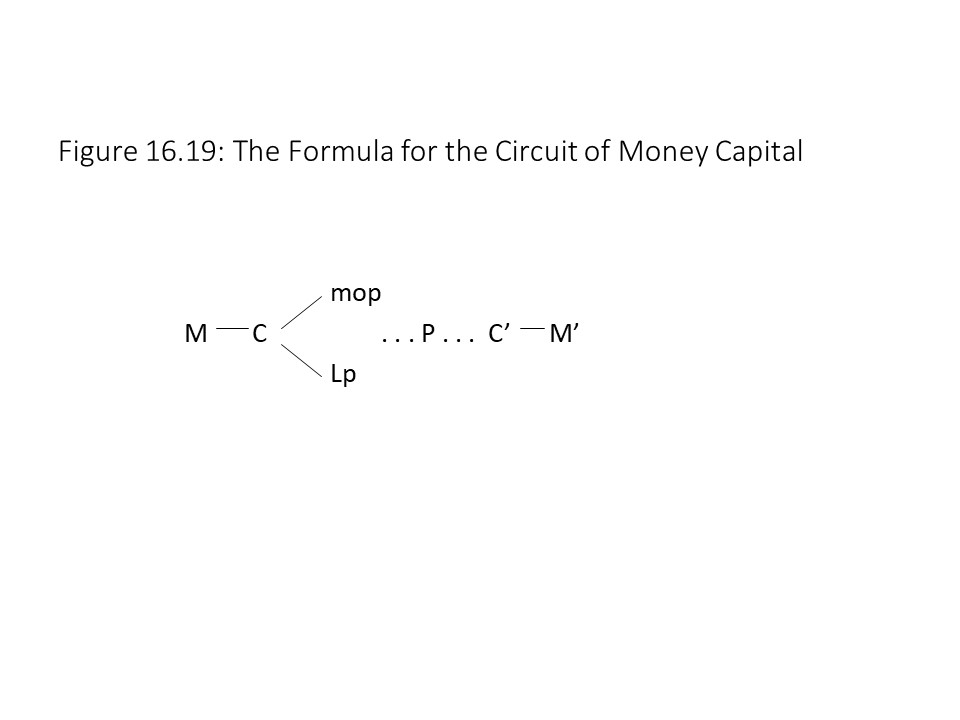 After circulation is interrupted with the production phase of the process (P) in Figure 16.19, the finished commodity (C’) is then transformed into a larger sum of money capital (M’). The surplus value is thus created in production and realized in exchange after production is complete. The reader should recall that it is the exploitation of labor-power that makes surplus value production and realization possible.
After circulation is interrupted with the production phase of the process (P) in Figure 16.19, the finished commodity (C’) is then transformed into a larger sum of money capital (M’). The surplus value is thus created in production and realized in exchange after production is complete. The reader should recall that it is the exploitation of labor-power that makes surplus value production and realization possible.
Industrial capitalists are capitalists who hire workers to produce commodities containing surplus value. Other kinds of capitalist exist as well. These capitalists receive a share of the surplus value that industrial capitalists appropriate in exchange for supporting the capitalist production process. For example, commercial capitalists (or merchant capitalists) hire workers who do not produce new commodities but who help to market and sell commodities. Because they assist with the realization of surplus value, industrial capitalists are willing to provide them with a share of the surplus value created in production, which becomes commercial profit. Moneylending capitalists provide industrial capitalists with the money capital they require to purchase means of production and labor-power. Because they help make possible the production of commodities containing surplus value, industrial capitalists are willing to provide them with a share of the surplus value created in production, which becomes interest.
Marxists argue that these two forms of capital, merchant capital and interest-bearing capital, are the oldest forms of capital. Ironically, it is necessary to understand how industrial capital produces surplus value if one is to understand the place of merchant capital and interest-bearing capital in modern capitalist societies. To understand the reason for this ironic result, consider the formula for the circuit of interest-bearing capital:
This circuit involves the transfer of interest-bearing capital to an industrial capitalist in monetary form. This part of the circuit (M-M) constitutes the granting of a loan. The circuit of industrial capital then follows with commodities (C) purchased and sold for a larger sum of money capital (M’). The initial loan amount (M) is then returned to the moneylending capitalist along with interest (ΔM) since M’ = M + ΔM as before. It is important to note that only the interest payment is shown here, as opposed to the entire surplus value produced, because it is the circuit of interest-bearing capital that is under investigation. In fact, the surplus value is a larger sum and the interest only represents a portion of the surplus value. That interest only represents a fraction of the surplus value (or profit) is a claim that was made in Chapter 15. Competition in the loan capital market determines the specific share that is paid as interest.
When we introduce commercial banks into the analysis, an additional type of capital comes into play. Bank capitalists advance bank capital with the aim of grabbing a share of the surplus value produced in the industrial sector. The circulation of bank capital is represented in Figure 16.20.
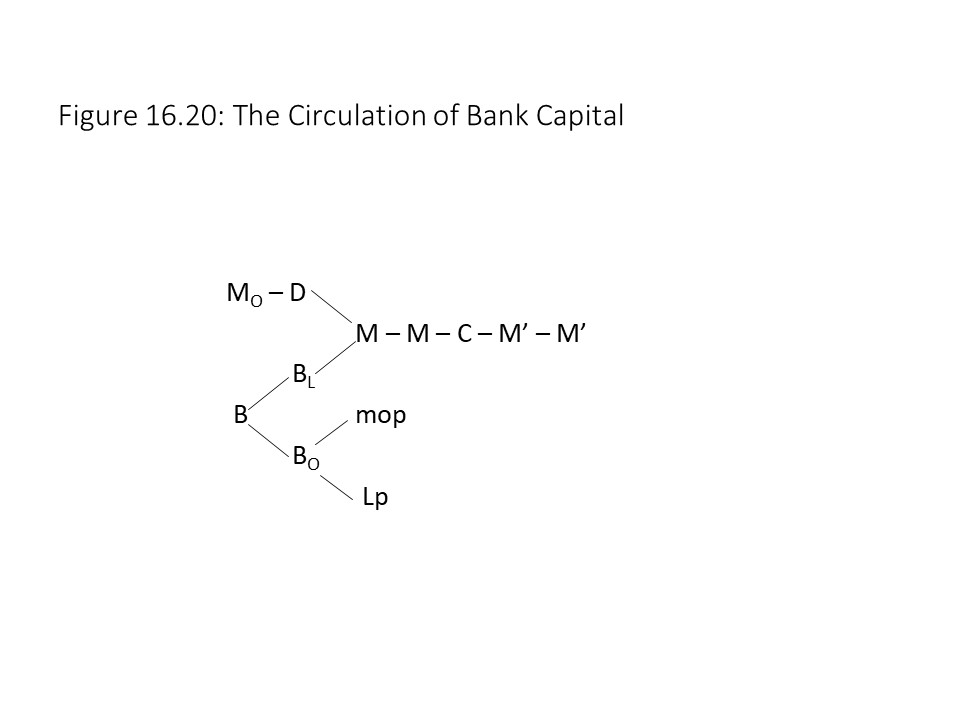 Figure 16.20 shows that depositors deposit their cash holdings (MO) in a commercial bank, which become deposit capital (D). The bank capitalist also advances bank capital (B), which then splits into two parts. Part of the bank capital is needed for the purchase of labor-power (Lp) and means of production (mop) to operate the bank. This part of the bank capital is referred to as bank operating capital (BO). The labor-power that is hired to operate the bank is unproductive labor-power in the sense that these workers do not produce surplus value. Instead, they help to make the production of surplus value possible. The means of production that are purchased are not used to produce commodities containing surplus value. The means of production that a bank purchases include office supplies, computers, and electricity. For simplicity, it is assumed that all the capital is circulating capital, which allows us to omit fixed capital such as a banking facility.
Figure 16.20 shows that depositors deposit their cash holdings (MO) in a commercial bank, which become deposit capital (D). The bank capitalist also advances bank capital (B), which then splits into two parts. Part of the bank capital is needed for the purchase of labor-power (Lp) and means of production (mop) to operate the bank. This part of the bank capital is referred to as bank operating capital (BO). The labor-power that is hired to operate the bank is unproductive labor-power in the sense that these workers do not produce surplus value. Instead, they help to make the production of surplus value possible. The means of production that are purchased are not used to produce commodities containing surplus value. The means of production that a bank purchases include office supplies, computers, and electricity. For simplicity, it is assumed that all the capital is circulating capital, which allows us to omit fixed capital such as a banking facility.
It is essential to recognize that the bank operating capital ends its circulation at this stage. Because the means of production and labor-power are not used to purchase valuable commodities, this capital does not return to the banking capitalist in this part of the circuit. Another part of the bank capital is advanced for lending, however, and may be referred to as bank loan capital (BL). It is combined with the deposit capital (D) to form the interest-bearing capital (M) described previously. The interest-bearing capital then passes through its circuit and returns with interest. The money capital that returns to the banking capitalist (M’) is equal to the principal amount of the loan (i.e., the bank loan capital plus the deposit capital advanced) made at the beginning of the circuit (BL+D) plus the gross bank profit (ΔM).
In this case, the gross bank profit must be sufficient to pay the operating expenses of the bank (BO) and return a net bank profit (ΔB) that is equal to the average profit in the economy.
Substituting the gross bank profit into the calculation of M’ yields the following result:
In other words, because the bank operating capital does not complete its circuit in the lower portion of Figure 16.20, it must return with the gross bank profit. If insufficient profit is realized to cover expenses and generate the average profit, then capitalists will cease to invest in the banking sector.
To understand how this analysis of commercial bank activity relates to the Marxist theory of financial markets presented in Chapter 15, we will initially simplify the discussion with the assumption that all bank capital is bank loan capital (i.e., no bank operating capital exists). Given this assumption, the principal amount of the loan (M) is equal to B+D since the entire bank capital is granted as a loan. The gross bank profit (ΔM) in this case is equal to the net bank profit (ΔB) because the bank need not earn enough profit to cover operating expenses, which are non-existent. We can use equations to express what has been stated thus far.
In Chapter 15, we explored a Marxist theory of interest rates. If we use the concepts developed in Chapter 16 to write an expression for the rate of interest, then it will be possible to link the two analyses. The rate of interest (i) is simply the amount of interest received on a loan (M) expressed as a percentage of the initial loan amount (M) as shown below:
At this stage, we only have a definition of the interest rate, and we lack a Marxist theory of its determination. To move in the direction of a theory, we divide the numerator and the denominator in the expression by the bank capital (B), which produces the following result:
To transform this definition of the rate of interest into a theory of the rate of interest, we need to recognize the numerator (i.e., the ratio of the net bank profit to the total bank capital) as the rate of profit on bank capital. In Marxian economics, competition among capitalists in an environment of unrestricted capital movements leads to an equalization of the profit rate throughout the economy. This rate of profit is referred as the general rate of profit (p). Of course, differences among profit rates across industries and capitalists always exist, and so the general rate of profit should be thought of as an average and the level towards which profits rates are constantly moving, even as unexpected factors cause deviations from this level.
Let’s assume that the general rate of profit (p) prevails in the banking sector. If bankers earn the general rate of profit, then we can substitute the general rate of profit for the profit rate expression in the numerator of our interest rate expression. Doing so provides us with an expression that we may refer to as the general rate of interest (ig).
The general rate of interest is the rate of interest that banks must charge borrowers to ensure that they earn the general rate of profit. It is a hypothetical rate of interest rather than the observable, market rate of interest (im). The market rate of interest is what banks earn on their loans. If the market rate of interest exceeds the general rate of interest, then banks earn more than the general rate of profit. If the market rate of interest is below the general rate of interest, then banks earn less than the general rate of profit.
The factors that determine the general rate of interest can be easily gleaned from its expression. If the general rate of profit (found in the numerator in the expression) rises, then the general rate of interest must rise to ensure that sufficient interest is received to guarantee that the bank earns the higher profit rate. If the general rate of profit falls, then the general rate of interest must fall because it takes less interest to ensure that the bank earns the lower profit rate. In Chapter 14 we learned that Marxian economists argue that the long-term tendency of the general rate of profit to fall in capitalist economies causes economic crises. Although various factors counteract this long-term tendency, it is a tendency that reasserts itself periodically. If the general rate of profit has a long-term tendency to fall and the general rate of interest is directly related to the general rate of profit, then the general rate of interest also has a long-term tendency to fall, subject of course to various counteracting tendencies.
One other factor that influences the general rate of interest is the deposit/bank capital ratio (D/B), which is found in the denominator of the expression. If the deposit/bank capital ratio rises, then the general rate of interest falls. This result is intuitive. A higher deposit/bank capital ratio means that banks are relying relatively more heavily on deposit capital when granting loans. These assets are very low-cost liabilities, particularly if they are checkable deposit liabilities that pay no interest, and so the banks require less interest to ensure that they receive the general rate of profit on bank capital. On the other hand, if the deposit/bank capital ratio falls, then banks are relying relatively more heavily on bank capital when granting loans and so must receive a higher rate of interest to ensure that the general rate of profit on bank capital is received.
It is one thing to assert that the general rate of interest is the rate of interest that will allow banks to earn the general rate of profit. It is another thing to assert that the market rate of interest will tend to move towards this level. To understand why the market rate of interest will gravitate towards the general rate of interest, consider what would happen if the market rate of interest was greater than the general rate of interest (im > ig). Figure 16.21 illustrates how capitalists in the industrial sector and in the financial sector will respond to this discrepancy.
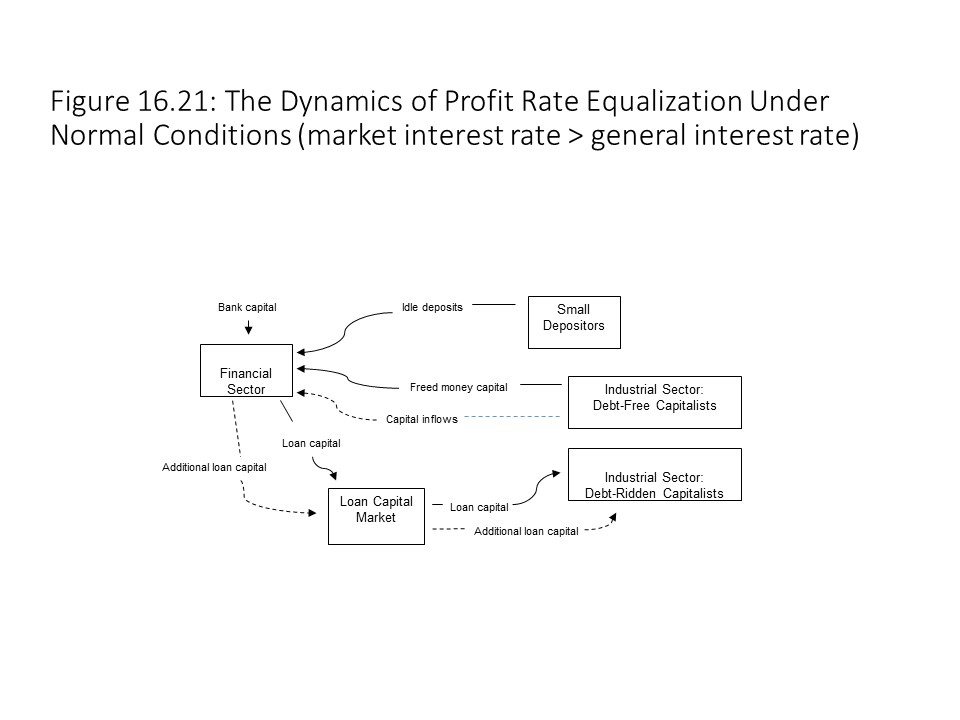 As previously explained, in this situation, banks will earn a profit rate that exceeds the general rate of profit. With unrestricted capital flows, industrial capitalists will begin to transfer capital out of industry and into finance. The inflow of capital into finance will cause banks to lend more in the loan capital market. The increased supply of loan capital will push down the market rate of interest in the direction of the general rate of interest. The process will continue until the market rate of interest equals the general rate of interest at which point the inflow of capital into finance will cease because the bank rate of profit is equal to the industrial rate of profit.
As previously explained, in this situation, banks will earn a profit rate that exceeds the general rate of profit. With unrestricted capital flows, industrial capitalists will begin to transfer capital out of industry and into finance. The inflow of capital into finance will cause banks to lend more in the loan capital market. The increased supply of loan capital will push down the market rate of interest in the direction of the general rate of interest. The process will continue until the market rate of interest equals the general rate of interest at which point the inflow of capital into finance will cease because the bank rate of profit is equal to the industrial rate of profit.
If the market rate of interest is below the general rate of interest, then the process works in reverse. That is, the bank rate of profit will be below the industrial rate of profit. Capital will flow out of finance and into industry. As the outflow of capital from finance continues, the supply of loan capital in the loan capital market will shrink, which puts upward pressure on the market rate of interest. The outflow of capital from finance will continue until the market rate of interest equals the general rate of interest at which point the bank rate of profit will once again equal the industrial rate of profit.[22]
It is also possible to incorporate the reserve requirement (R) into the analysis. If banks are required to keep a fraction of their deposit liabilities (D) in the form of reserves, then they will only be able to lend their excess reserves, which are equal to 1-R times the deposit liabilities. The expression for the general rate of interest, considering the reserve requirement, thus changes to the following:
Our earlier expression for the general rate of interest is a special case of this expression where the reserve requirement is zero (R=0). Previously, banks could advance the entire deposit capital (D). Now they can only advance the excess reserves of (1-R)D. Mathematically, it should be clear that if R rises, then the general rate of interest will rise. That is, if banks are required to hold more reserves and thus lend less, then they must earn a higher interest rate on their loans to ensure that they receive the general rate of profit. If R falls, then banks can lend more and the rate of interest they require to obtain the general rate of profit is lower.
It is also worth noting that the maximum value of the general rate of interest is the general rate of profit. The maximum value is reached when banks are required to hold 100% of their deposits as reserves (R=1). In that case, they only lend bank capital and so must receive an interest rate equal to the general profit rate if they are to earn that profit rate. The minimum value of the general rate of interest is the expression we discussed previously where the reserve requirement was equal to zero (R=0). It is the lower bound because the banks can lend all their deposit capital to borrowers. The upper and lower bounds of the general rate of interest may be expressed as follows:
A final modification that we can make to the general rate of interest expression involves the incorporation of bank operating capital (BO), which has been assumed to equal zero thus far. If bank operating capital is positive, then the bank must receive it as part of gross bank profit (ΔM). Also, if bank operating capital is positive, then the bank cannot lend its entire bank capital but only a portion that we call the bank loan capital (BL). Making these adjustments to the general rate of interest expression and dividing the numerator and denominator by the bank capital yields the following result:
This new expression for the general rate of interest shows that a rise in bank operating capital will raise the general rate of interest. This result is expected because higher operating costs mean that banks require a higher interest rate to cover these expenses and obtain the general rate of profit on bank capital. Also, because the total bank capital equals the sum of bank operating capital and bank loan capital, a rise in bank operating capital involves a reduction in bank loan capital, which also raises the general rate of interest. That is, when banks lend less, they require a higher rate of interest to obtain the same general rate of profit. Conversely, a reduction in bank operating capital will lower the general rate of interest because banks have lower expenses and can manage with a lower rate of interest. They also lend more and so can obtain the general rate of profit when they charge a lower interest rate.
When the market rate of interest and the general rate of interest are equal, we have seen that no capital movements will occur between industry and finance. The reason is that the profit rate in the banking sector is equal to the profit rate in the industrial sector, and so capitalists have no incentive to reallocate capital across sectors. The static situation described here can be illustrated with the numerical example in Table 16.3 that uses the final expression for the general rate of interest developed in this chapter.
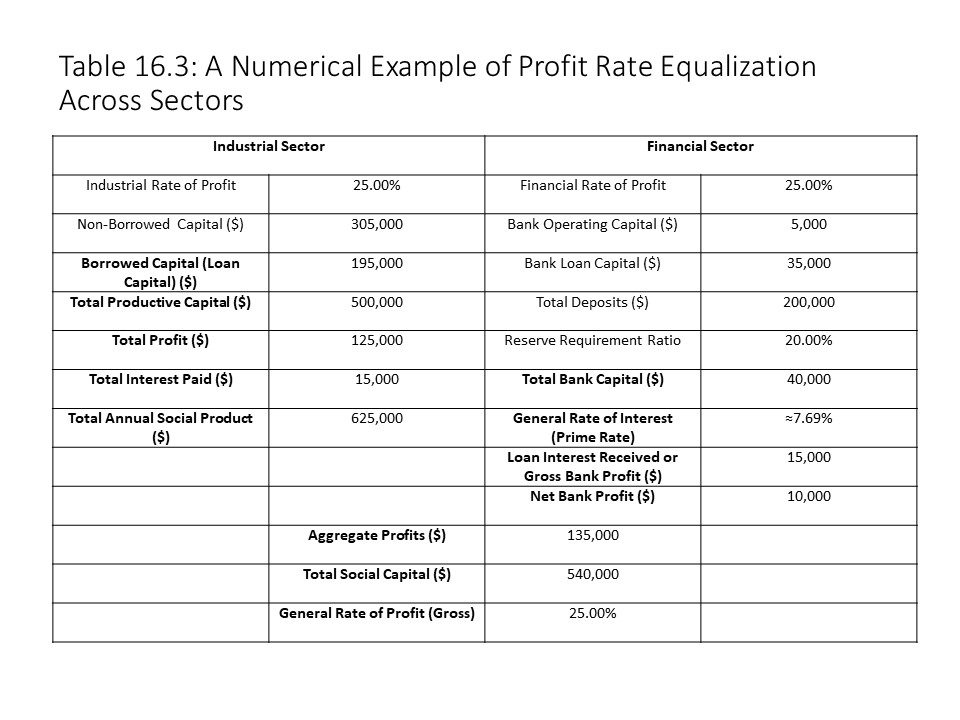 The two-sector example shown in Table 16.3 treats all items except for the bold-faced items as given. The bold-faced items are calculated using the definitions in this chapter. For example, it is assumed that a 25% rate of profit prevails in the two sectors. Summing together the given bank operating capital and bank loan capital, we obtain the total bank capital. To obtain the borrowed capital in the industrial sector, we calculate the sum of the bank loan capital and the excess reserves, BL+(1-R)D, using the given required reserve ratio (R). The sum of the borrowed capital and the given non-borrowed capital in the industrial sector equals the total productive capital. The total industrial profit is calculated as the product of the industrial profit rate and the total productive capital. The general rate of interest is calculated using the final formula for the general rate of interest that we developed. The total interest paid in the industrial sector is the product of the general rate of interest and the borrowed capital. The total annual social product is the sum of the total productive capital and the total industrial profit. The gross bank profit is the same as the interest that industrial capitalists pay to the banking capitalists. The net bank profit is the gross bank profit minus the bank operating capital. The aggregate profits are the sum of the net bank profits and the industrial profits. The total social capital is the sum of the total productive capital and the total bank capital. The gross general rate of profit is the ratio of the aggregate profits to the total social capital. The reader should carry out these calculations to test his or her understanding of the relationships. Table 16.4 provides formulas for each of the calculations.
The two-sector example shown in Table 16.3 treats all items except for the bold-faced items as given. The bold-faced items are calculated using the definitions in this chapter. For example, it is assumed that a 25% rate of profit prevails in the two sectors. Summing together the given bank operating capital and bank loan capital, we obtain the total bank capital. To obtain the borrowed capital in the industrial sector, we calculate the sum of the bank loan capital and the excess reserves, BL+(1-R)D, using the given required reserve ratio (R). The sum of the borrowed capital and the given non-borrowed capital in the industrial sector equals the total productive capital. The total industrial profit is calculated as the product of the industrial profit rate and the total productive capital. The general rate of interest is calculated using the final formula for the general rate of interest that we developed. The total interest paid in the industrial sector is the product of the general rate of interest and the borrowed capital. The total annual social product is the sum of the total productive capital and the total industrial profit. The gross bank profit is the same as the interest that industrial capitalists pay to the banking capitalists. The net bank profit is the gross bank profit minus the bank operating capital. The aggregate profits are the sum of the net bank profits and the industrial profits. The total social capital is the sum of the total productive capital and the total bank capital. The gross general rate of profit is the ratio of the aggregate profits to the total social capital. The reader should carry out these calculations to test his or her understanding of the relationships. Table 16.4 provides formulas for each of the calculations.
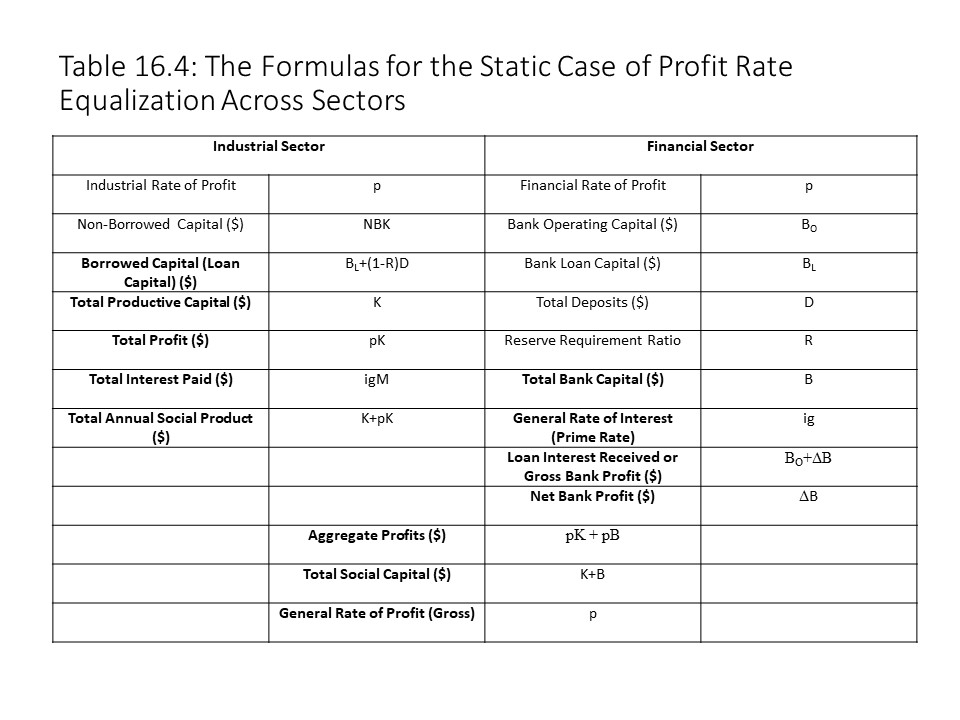 To summarize the analysis in this section, the exploitation of labor-power in the industrial sector generates the surplus value that is appropriated as profit in the industrial sector and then as interest in the banking sector. The banking sector is parasitic in that it does not produce surplus value but helps make the production of surplus value possible when it grants loans to the industrial capitalists who use the funds to purchase labor-power and the means of production. To ensure the continuation of such loans, the industrial capitalists allow the banking capitalists to share in the surplus value that they appropriate from the working class.
To summarize the analysis in this section, the exploitation of labor-power in the industrial sector generates the surplus value that is appropriated as profit in the industrial sector and then as interest in the banking sector. The banking sector is parasitic in that it does not produce surplus value but helps make the production of surplus value possible when it grants loans to the industrial capitalists who use the funds to purchase labor-power and the means of production. To ensure the continuation of such loans, the industrial capitalists allow the banking capitalists to share in the surplus value that they appropriate from the working class.
It is helpful to reflect on the relationship between this Marxian analysis of financial markets and the analysis of the rate of interest in Chapter 15. In Chapter 15, a theory is presented that shows how the market rate of interest fluctuates over time as the level of production changes. That is, the business cycle is assumed in that analysis, and the rate of interest fluctuates due to discrepancies between the supply and demand for loanable money capital. In Chapter 16, however, the business cycle is not responsible for changes in the market rate of interest. It is capital’s search for the highest rate of profit that is responsible for adjustments of the market rate of interest to the general rate of interest. Even if we assume an abstract situation in which the level of production is stable and the business cycle is not operative, the search for a maximum profit rate still applies, and capital will flow between industry and finance accordingly. The general rate of interest then is the average rate of interest towards which the market rate of interest moves. Deviations from this level are due to discrepancies in the loanable money capital market over the course of the business cycle.
F ollowing the Economic News [23]
A recent news article in USA TODAY explains that the biweekly pay schedule that affects millions of American workers is an antiquated practice and burdensome workplace norm. Tim Chen explains that digital banking has made it possible to pay workers more quickly for the work they perform. Because many workers are living paycheck to paycheck, Chen explains that approximately “12 million Americans use payday loans to cover emergencies and living expenses at effective interest rates that exceed 300 percent.” For neoclassical economists, these loans increase the welfare of all involved. Lenders transfer funds from those who do not have a current use for them to those who do. Such transfers of funds improve efficiency and social well-being. It is an example of Adam Smith’s invisible hand applied in the financial marketplace. Both borrower and lender gain as they each serve the other’s interest while only thinking of their own interest. From a Marxian perspective, payday loans force workers into a debt trap. Capitalists withhold wages for half the month, which pressures workers to borrow at very high interest rates. As Chen explains, when their paychecks are finally deposited in their bank accounts, many workers are not able to repay their payday loans, which leads to additional borrowing, more fees, and a continuous cycle of debt accumulation. Chen argues that loan fees cost Americans $9 billion annually with an additional $14 billion annually for overdraft fees. Chen explains that millions of Americans also lack bank accounts, which leads them to use “costly check-cashing services to get same-day access to their funds.” Chen cites the Bookings Institution, which claims that interest payments and fees can amount to $40,000 during a worker’s lifetime. Because these fees and interest payments are paid from workers’ wages, they represent an example of how financial institutions can recover some of the income that is distributed to workers for the necessary labor they perform. Just as industrial capitalists appropriate surplus labor in the form of profit, the financial capitalists can appropriate a portion of the necessary labor of workers in the form of interest. Neoclassical economists, on the other hand, view the fees and interest payments as compensation to lenders for their willingness to grant risky loans to people who might not be able to repay them. Without such compensation, neoclassical economists argue, no lenders will have an incentive to grant these loans and both borrowers and lenders will be harmed. Using different theoretical perspectives, we reach different conclusions about the desirability of specific types of market transactions.
Summary of Key Points
- The three functions of money in neoclassical theory are medium of exchange, unit of account, and store of value.
- The double coincidence of wants problem exists in barter economies because commodity owners must be able to find other commodity owners who possess the commodities they want and who are willing to exchange those commodities for what they own.
- Commodity money is an object with intrinsic value, convertible paper money is paper that is convertible into commodity money, and inconvertible paper money is paper that is not convertible into anything else.
- The M1 money supply includes publicly held currency and checkable deposits; the M2 money supply includes M1 and savings deposits, small time deposits, MMDAs, and MMMFs; the M3 money supply includes M2 and large time deposits.
- The Ma definition of the money supply is like the M2 definition of the money supply except that: 1) it includes time deposits and federal savings bonds at current redemption rates; 2) it includes the cash surrender values of life insurance policies; and 3) it subtracts the demand deposits of thrift institutions to avoid double counting.
- In a 100% reserve banking system, the entire money supply is backed up with bank reserves whereas in a fractional reserve banking system, only a fraction of the money supply is backed up with bank reserves.
- The balance sheet of a bank lists its assets, liabilities, and net worth, and the total assets must always equal the sum of the liabilities and net worth.
- Securities, loans, and cash reserves are the most important assets for banks. Deposits and borrowings are the most important liabilities for banks.
- Successful banks must manage their assets, liabilities, degree of liquidity, and bank capital simultaneously.
- Banks are legally required to hold a specific fraction of their deposits as reserves, which is referred to as the reserve requirement.
- Commercial banks increase the M1 money supply when they grant loans to borrowers, purchase bonds from bond dealers, and allow transfers from savings accounts into checking accounts or currency. The opposite actions reduce the M1 money supply.
- When banks acquire new reserves, the rounds of successive lending that are initiated increase the M1 money supply by a multiple of the initial increase in bank reserves.
- Whereas industrial capitalists appropriate the surplus value that their workers produce, commercial capitalists, moneylending capitalists, and bank capitalists receive a share of the surplus value that industrial capitalists appropriate.
- The general rate of interest is the rate of interest that prevails when the rate of profit in the financial sector is the same as the rate of profit in the industrial sector.
List of Key Terms
Medium of exchange
Barter economy
Double coincidence of wants problem
Unit of account
Store of value
Commodity money
Convertible paper money
Inconvertible paper money
Fiat money
Digital currencies
Mining
Money supply
Money stock
Liquidity
Currency
M1 money supply
Thrift institutions
Savings and loan associations
Credit unions
M2 money supply
Certificates of deposit (CDs)
Money market mutual funds (MMMFs)
Money market deposit accounts (MMDAs)
M3 money supply
Cash surrender values
Austrian definition of the money supply (Ma)
100% reserve banking system
Bank run
Fractional reserve banking system
Balance sheet
Assets
Liabilities
Net worth (equity)
Balance sheet equation
Insolvent
Securities
Loans
Default
Loan losses
Cash reserves
Deposits
Borrowings
Federal funds market
Federal funds rate
Discount loans
Discount rate
Bank capital
Reserve requirement
Excess reserves
Multiple expansion of bank deposits
Simple deposit multiplier
Money multiplier
Industrial capitalists
Commercial capitalists
Commercial profit
Moneylending capitalists
Merchant capital
Interest-bearing capital
Bank capitalists
Bank operating capital
Unproductive labor-power
Bank loan capital
Rate of interest (i)
General rate of profit (p)
General rate of interest (ig)
Problems for Review
1.Can you think of an asset that is a good store of value but not a good unit of account or medium of exchange? Can you think of an asset that is a good unit of account but not a good medium of exchange or store of value? Can you think of an asset that is a good medium of exchange but not a good unit of account or store of value?
2. Suppose that you are presented with the following information:
- Savings deposits = $9 trillion
- Cash surrender values of life insurance policies = $2.5 trillion
- Checkable deposits = $3 trillion
- Large time deposits (face value) = $1.5 trillion
- Small time deposits (face value) = $4 trillion
- Large time deposits (current redemption value) = $1 trillion
- Publicly held currency = $1.5 trillion
- Savings bonds (current redemption value) = $3 trillion
- MMDAs = $3.5 trillion
- MMMFs = $2.5 trillion
- Small time deposits (current redemption value) = $3.5 trillion
- Demand deposits that thrift institutions hold in commercial banks = $1 trillion
Calculate the M1 money supply.
Calculate the M2 money supply.
Calculate the M3 money supply.
Calculate the Ma money supply.
3. Suppose that you are presented with the following information:
- A bank has $25 billion in cash reserves.
- A bank has issued checkable deposits of $41 billion.
- A bank has borrowings of $62 billion.
- A bank has issued savings deposits of $42 billion.
- A bank has $48 billion in securities.
- A bank has $66 billion in loan assets.
Create a balance sheet for the bank. Determine the level of bank capital. Does the balance sheet equation hold with the answer you have provided? What is the bank’s situation like?
4. Suppose that a depositor decides to transfer $3000 from a checking account to a savings account. Create a balance sheet for the bank, and show how the balance sheet will be affected due to this change. Only list the changes on your balance sheet. Then explain what will happen to the M1 and M2 money supplies.
5. Suppose a bank purchases $60,000 in bonds from a bond dealer who has a checking account at the bank. Create a balance sheet for the bank, and show how the balance sheet will be affected due to this change. Only list the changes on your balance sheet. Then explain what will happen to the M1 and M2 money supplies.
6. Suppose that a borrower repays a loan in the amount of $80,000. Create a balance sheet for the bank, and show how the balance sheet will be affected due to this change. Only list the changes on your balance sheet. Then explain what will happen to the M1 and M2 money supplies.
7. Suppose that a borrower makes a cash withdrawal of $4000 from a savings account. Create a balance sheet for the bank, and show how the balance sheet will be affected due to this change. Only list the changes on your balance sheet. Then explain what will happen to the M1 and M2 money supplies.
8. Suppose banks acquire $50 billion in new reserves, and the reserve requirement ratio is 6%. What will be the impact on the total deposits in the system, assuming all excess reserves are loaned to borrowers and the public redeposits all the borrowed funds in the banking system?
9. Suppose that you know the following information about the banking system. Use the information to complete the rest of the table.

- The three functions of money discussed in this section are universally recognized in neoclassical textbooks. ↵
- Mishkin (2006), p. 46, emphasizes the reduction in search time as an efficiency-enhancing characteristic of money. ↵
- Mishkin (2006), p. 46, also refers to the promotion of specialization as a second efficiency-enhancing characteristic of money. ↵
- See Marx (1990), p. 227-244, for a detailed account of these functions. ↵
- This example is found in OpenStax (2014), p. 617. ↵
- The Federal Reserve concluded that “M3 does not appear to convey any additional information about economic activity that is not already embodied in M2” (Federal Reserve Statistical Release. H.6 Money Stock Measures: Discontinuance of M3. November 10, 2005. Revised March 9, 2006. Web. Accessed on January 20, 2018. https://www.federalreserve.gov/Releases/h6/discm3.htm). ↵
- Rothbard (1978), p. 151. ↵
- Ibid. pp. 145. ↵
- Ibid. pp. 146-148. ↵
- Ibid. pp. 148. ↵
- Ibid. pp. 149. ↵
- Ibid. pp. 150. ↵
- Ibid. pp. 150. ↵
- Ibid. pp. 151. ↵
- Ibid. pp. 151. ↵
- Ibid. pp. 151-152. ↵
- This imaginative approach is inspired by the goldsmith story that is found in neoclassical textbooks. See Even, Louis. "The Goldsmith Who Became a Banker - A True Story." Cahiers du Crédit Social. October 1936.↵
- It is common for neoclassical textbooks to present a consolidated balance sheet for commercial banks and then discuss the different balance sheet items. For example, see Samuelson and Nordhaus (2001), p. 522, and Mishkin (2006), p. 201-205. Mishkin (2006), p. 201-205, and Hubbard and O’Brien (2019), p. 872-874, provide detailed discussions of each balance sheet item, which are like the approach of this section. ↵
- Frederic Mishkin (2006), p. 208, identifies the corresponding types of management for these objectives as asset management, liability management, liquidity management, and capital adequacy management. ↵
- A higher demand for loanable funds and a higher supply of bonds is also expected, but we emphasize the other shifts because their larger impact brings about contractions of the financial markets consistent with the monetary contraction. ↵
- The theory presented in this section draws from the following source: Saros, Daniel E. "The Circulation of Bank Capital and the General Rate of Interest." Review of Radical Political Economics, 45 (2), Spring 2013: 149-161. The final, definitive version is available at online.sagepub.com/. journals.sagepub.com/doi/full/10.1177/0486613412458647↵
- The analysis presented here is a simplification. A complicating factor is that when capital flows into or out of finance, the level of bank capital changes, which alters the general rate of interest as well. I have explained how to analyze the simultaneous movements in the general rate of interest and the market rate of interest in Saros (2013), p. 158-159. ↵
- Chen, Tim. “Pay workers in real time, end debt cycle; Help people access their earnings and avoid high interest payday loans.” USA TODAY. First Edition. 25 Oct. 2018. ↵


