17: Monetary Theories and the Role of the Central Bank
- Last updated
- Save as PDF
- Page ID
- 46265
Goals and Objectives:
In this chapter, we will do the following:
- Identify the organizational structure and functions of the Federal Reserve
- Analyze the tools that the central bank uses to influence the financial markets
- Examine the neoclassical approach to monetary policy using an exogenous money supply
- Inspect the connection between the Quantity Theory of Money and the AD/AS Model
- Explore a Post-Keynesian approach to monetary policy using an endogenous money supply
- Investigate a Marxian theory of fiat money and relate it to U.S. economic history
- Link the monetary policy tools to the Marxian theory of financial markets
In Chapter 16, we explored different methods of measuring the quantity of money and how commercial banks influence those different measures. We also looked at how commercial banking activities influence the financial markets from neoclassical and Marxian perspectives. In this chapter, a major purpose is to explore the role of the central bank in the determination of the money supply. All modern capitalist economies have a central bank and so an analysis of modern banking systems must incorporate its role into any meaningful analysis. Once we understand the role the central bank plays in the determination of the money supply, we will then be able to understand how the central bank influences the overall economy. Of course, our understanding depends on our theoretical lens, and so we will explore this question from neoclassical, Post-Keynesian, and Marxian perspectives.
T he Organizational Structure and Functions of the Federal Reserve
Modern capitalist nations have central banks that are responsible for the management of the money supply and the conduct of monetary policy. Monetary policy refers to the use of money supply changes to influence aggregate production, the aggregate price level, and the level of unemployment. In Japan, the central bank is the Bank of Japan. In England, the central bank is the Bank of England. In the eurozone (i.e., in the European nations that have adopted the euro), the central bank is the European Central Bank. In the United States, the central bank is the Federal Reserve (also known as the Fed).
The Federal Reserve was created by an Act of Congress in 1913. After the 1907 financial crisis, private bankers recognized that some central control of the money supply was needed to prevent bank panics from becoming major financial crises. The notion of a central bank that could intervene during a bank panic as a lender of last resort to stabilize the financial markets was perceived to be necessary. Rather than centralize financial power in a single central bank, however, a compromise was struck that created 12 Federal Reserve Banks in 12 distinct Federal Reserve districts throughout the nation. The 12 Federal Reserve Banks are in the following cities:
- Atlanta
- Boston
- Chicago
- Cleveland
- Dallas
- Kansas City
- Minneapolis
- New York
- Philadelphia
- Richmond
- San Francisco
- St. Louis
Each Federal Reserve Bank has a Board of Directors and a Board-appointed Federal Reserve Bank President. In addition to the 12 Federal Reserve Banks, the Federal Reserve System has its headquarters in Washington, DC. A Federal Reserve Boardof Governors, which consists of appointed officials, governs the entire system. The Board of Governors consists of seven members that the President of the United States appoints for 14-year staggered terms subject to U.S. Senate confirmation. The staggering of the terms guarantees that one Governor’s term expires every two years, which ensures a significant degree of continuity on the Board. If, for example, the terms of all seven Governors expired in the same year, then an entirely new Board would be appointed that year, and it would be difficult for the new Governors to benefit from the knowledge and experience of past Governors. The President of the United States also appoints one Governor to serve as Chair of the Federal Reserve Board and another Governor to serve as Vice-Chair. The terms of Chair and Vice Chair are four-year, renewable terms. Generally, when the term of a Chair expires, they are either reappointed or they leave the Board altogether. The position of Federal Reserve Board Chair is the most powerful position in the Federal Reserve system. The Fed Chair serves as the spokesperson for the Fed. Past Chairs have included Alan Greenspan, Ben Bernanke, and Janet Yellen. The Fed Chair in 2018 is Jerome Powell.
A second governing body within the Federal Reserve system is the Federal Open Market Committee (FOMC). The FOMC consists of 12 members, including the seven members of the Board of Governors, the President of the New York Federal Reserve Bank, and four other Federal Reserve Bank Presidents who serve on a one-year, rotating basis. The FOMC meets about every 6 weeks at the Federal Reserve headquarters in Washington, DC and is responsible for conducting all Fed interventions in the bond market. Federal Reserve bond market interventions are conducted through the New York Fed, which is the reason that the New York Fed President is the only permanent member of the FOMC. The New York Fed is important for several other reasons, as Frederic Mishkin explains, including its role as a gold repository, its conduct of foreign exchange market interventions, and its proximity to the largest financial institutions in the world.[1]
The legal status of the Fed is also somewhat unusual. It is regarded as a quasi-public institution in that it is privately owned but publicly controlled. The owners of the Fed are the private commercial banks within the Federal Reserve system. The banks own stock in the Fed and may receive profit distributions each year if the Fed earns a profit, subject to maximum limits. The legal mandate of the Fed is not to make a profit, however, but to serve the public interest.[2] Control of the system rests with public officials, and so it is neither a purely private nor a purely public institution.
Because the officials that control the Federal Reserve system are appointees with long terms in office, the Fed operates with a considerable degree of independence. That is, elected officials have relatively little control of Fed policy. Of course, Congress can change the Federal Reserve Act or even abolish the Fed if it repeals that legislation, but such changes require major legislative action. As the law stands, elected officials can do little to alter monetary policy aside from waiting until new Governors are appointed to the Federal Reserve Board. The notion of central bank independence is a controversial one. Its strength is simultaneously its weakness. Independence allows the Fed to pursue politically unpopular policies that serve the public interest, but the lack of democratic control of these decision makers makes many people uncomfortable as it seems to conflict with the principles of American democracy. It does not seem possible to resolve this question to the satisfaction of all parties. In any case, the general trend throughout the world in recent decades has been towards greater central bank independence to avoid harmful economic policies, especially those that encourage inflation.
The Fed performs several key functions. Almost all Fed functions can be inferred from the elements on its balance sheet. The one function of the Fed that is not clearly reflected in the Fed’s balance sheet is its role as a supervisor of banks. The Fed shares this responsibility with other state and federal government agencies, which involves monitoring levels of bank capital, reserves, and risk. Figure 17.1 shows the balance sheet of the Federal Reserve. The figure combines all assets, liabilities, and net worth for all 12 Federal Reserve Banks.

On the asset side of the Fed’s balance sheet, we see loans to commercial banks. The loans to commercial banks represent the original function of the Fed as lender of last resort. During a financial panic, banks cease to lend due to fear that borrowers will default on those loans. By granting loans to banks, the Fed can help restore confidence in the financial system. Banks will feel reassured that the banks to whom they lend will receive assistance from the Fed, if necessary, so that they can repay their loans with interest. Because the loans that the Fed grants to banks are interest-bearing loans, they are assets for the Federal Reserve. The reader might be surprised that the loan assets of the Fed only amount to $54 million, which is a small sum in comparison with other items on the asset side of the balance sheet. Because the U.S. economy is not experiencing a financial crisis, the lender of last resort role of the Fed is not especially necessary. Another important reason for the low figure is that the Fed encourages banks to borrow from other banks in the federal funds market. It does so by charging an interest rate on loans to banks that is higher than the federal funds rate. Therefore, banks voluntarily choose to borrow from one another rather than from the Fed.
The Federal Reserve is also an issuer of currency. It is important to note that the Fed does not print money, which is a common misconception. The Fed does not print U.S. dollars. It is the Bureau of Engraving and Printing within the U.S. Department of Treasury that is responsible for that duty. Once the dollars are printed, however, a Federal Reserve Bank must issue them. If you look at a U.S. dollar, you can see which Federal Reserve Bank issued your bill. You will also see the words “Federal Reserve Note” at the top of your U.S. dollar. In fact, Federal Reserve Notes are U.S. dollars. The function of the Fed as an issuer of currency also shows up on the liabilities side of the Fed’s balance sheet. The Federal Reserve Notes (outstanding) entry on the balance sheet shows how many U.S. dollars have been issued. It might seem strange that Federal Reserve Notes are treated as a liability of the Fed. If the Fed notes represented convertible paper money, then it would be easy to understand why they are treated as liability. They would represent a claim to so much gold or silver on the asset side of the Fed’s balance sheet. Because U.S. dollars are fiat money, they do not represent a claim to gold, but from a conceptual point of view, you can think of them as representing a claim to the assets of the Fed even though they are not directly redeemable. Incidentally, the Fed does own gold and other precious metals, which are included in the Other category on the asset side of the Fed’s balance sheet.
The reader might be puzzled that coins are found on the asset side of the Fed’s balance sheet even as U.S. dollars are treated as a liability of the Fed. The reason is that while Federal Reserve Banks issue U.S. dollars, the Fed does not issue coins. The U.S. Treasury mints and issues coins. Therefore, coins are a liability of the Treasury, and they are treated as an asset when the Fed acquires them.
The Fed also serves as a banker for commercial banks. This role is reflected in the reserves of commercial banks, which is a liability on the Fed’s balance sheet. The Fed owes banks that transfer currency and other assets to the Fed. For example, if the Fed buys securities from a commercial bank, then it may pay the bank by crediting the bank’s reserve account. This operation increases the Fed’s assets and liabilities. It reduces the bank’s assets because it loses securities, but it also increases its assets by an equal amount because it gains reserves. Alternatively, the bank might transfer currency to the Fed, which leaves the Fed’s liabilities unchanged. It reduces the Fed’s liabilities because its outstanding Federal Reserve Notes decline, but its liabilities increase by an equal amount as it credits the bank’s reserve account. The bank loses currency but gains reserves and so its assets remain the same overall. For many years, banks were not paid interest for the reserves held at the Fed. In 2008, this policy changed, and banks have since earned interest on their Fed reserve holdings.
The Fed also serves as a processor of checks as explained in Chapter 16. When an account holder writes a check against a checkable deposit, the bank that receives the check sends it to the Fed for processing. The Federal Reserve Bank in that district increases the reserves of the recipient bank and debits the reserves of the bank with the account against which the check is drawn. The changes to bank reserves do not occur immediately, however, and so the reserves of the recipient bank increase before the reserves of the other bank are debited. During this period, the Fed acquires a new asset referred to as items in process of collection. The items in process of collection on the Fed’s balance sheet thus reflects this function of the Fed.
The Fed also serves as a banker for the federal government. Individuals and firms cannot open bank accounts at Federal Reserve Banks. Only commercial banks in the Federal Reserve system and the U.S. government have this privilege. The U.S. Treasury collects hundreds of billions of dollars in tax revenue each year. These funds must be deposited somewhere, and the U.S. Treasury account at the Fed is where these funds are deposited. U.S. Treasury deposits are a liability for the Fed because the Fed owes the Treasury once these deposits are received. If they are transfers from commercial banks, then the Fed’s reserve liabilities decline and its Treasury deposit liabilities increase by an equal amount.
One other asset that appears on the Fed’s balance sheet is foreign currency-denominated assets. Such assets reflect the Fed’s history of intervention in foreign exchange markets. The Fed has the power to intervene on a massive scale in foreign currency markets. By doing so, it can alter the foreign exchange values of the U.S. dollar and other currencies for which it trades. A deliberate manipulation of the U.S. exchange rate can make U.S. exports (or U.S. imports) cheaper or more expensive. Such changes can have an impact on aggregate spending in the U.S. and thus aggregate output, employment, and the price level as discussed in Chapter 13. In an era of floating exchange rates, however, the Fed is not actively involved in managing the foreign exchange value of the U.S. dollar even though it retains the power to do so.
The Primary Central Bank Tools of Monetary Policy
The last function of the Fed that we can observe in the Fed’s balance sheet is its function as regulator of the money supply. This regulatory function includes the three primary tools of monetary policy.[3] The first monetary policy tool and the tool that has been the most important in recent decades is open market operations. Open market operations refer to the Fed’s bond market interventions (i.e., the purchases and sales of government securities). When the Fed purchases government bonds from commercial banks, it pays the banks with reserves (i.e., it credits their reserve accounts). The additional reserves can be used to grant loans, which expands the money supply. Alternatively, if the Fed sells government securities to commercial banks, then banks will pay for the bonds using reserves (i.e., it debits their reserve accounts). Faced with dwindling reserves, banks contract their lending, and the money supply falls. Hence, the securities and reserves items on the Fed’s balance sheet represent the open market operations of the Fed and thus its role as regulator of the money supply.
A second monetary policy tool of the Fed is discount lending. Discount loans are loans that the Fed grants to commercial banks. Sometimes these loans are granted during financial crises and are consistent with the lender of last resort function. Sometimes the loans are granted during periods of economic and financial stability but to banks that are nevertheless in financial trouble. When the loans are granted, the Fed adds to the banks’ reserve accounts. The banks that receive these reserves can then grant additional loans to borrowers, which expands the money supply. Although the Fed cannot force banks to borrow, the Fed can reduce the discount rate, which is the interest rate charged on discount loans. Because the loans are cheaper when the discount rate falls, banks are more inclined to borrow from the Fed. Alternatively, if the discount rate increases, then banks are less inclined to borrow from the Fed, and discount lending and bank lending contract, which reduces the money supply. Hence, the loans to commercial banks and the reserves of commercial banks on the Fed’s balance sheet reflect the Fed’s role as regulator of the money supply.
A third monetary policy tool of the Fed is the reserve requirement ratio (R). When the Fed lowers the reserve requirement ratio, commercial banks are not required to hold as many reserves. Commercial banks thus have more excess reserves, which they lend to borrowers, thereby expanding the money supply. Alternatively, if the Fed raises the reserve requirement ratio, then banks have fewer excess reserves, and they need to hold more reserves in their accounts with the Fed. To do so, they contract their lending, which reduces the money supply. Hence, the reserves of commercial banks on the Fed’s balance sheet reflects the Fed’s role as regulator of the money supply.
To see the impact of each of these monetary policy tools on the money supply, just consider the balance sheets of a commercial bank and the Fed. When the Fed engages in open market operations, its bond market purchases and sales influence the reserves in the banking system. For example, suppose that the Fed buys $8,000 in bonds from commercial banks. The impact on the Fed’s balance sheet and the commercial bank’s balance sheet are shown in Figure 17.2.
 Figure 17.2 shows that the Fed gains securities in the amount of $8,000 and then credits the account of the bank as payment for the securities. The Fed’s assets and liabilities thus increase by an equal amount. The commercial bank, on the other hand, loses an asset when it sells the securities, but it gains an asset in the form of additional reserves. If the bank was meeting its reserve requirement previously, then these additional reserves constitute excess reserves for the bank. If the bank uses the excess reserves to grant loans, then new deposits are created and the M1 money supply expands. This process is also likely to lead to additional lending by other banks and the multiple expansion of bank deposits described in Chapter 16.
Figure 17.2 shows that the Fed gains securities in the amount of $8,000 and then credits the account of the bank as payment for the securities. The Fed’s assets and liabilities thus increase by an equal amount. The commercial bank, on the other hand, loses an asset when it sells the securities, but it gains an asset in the form of additional reserves. If the bank was meeting its reserve requirement previously, then these additional reserves constitute excess reserves for the bank. If the bank uses the excess reserves to grant loans, then new deposits are created and the M1 money supply expands. This process is also likely to lead to additional lending by other banks and the multiple expansion of bank deposits described in Chapter 16. Figure 17.3 shows that the Fed loses securities in the amount of $4,000 and then debits the account of the bank that is paying for the securities. The Fed’s assets and liabilities thus decrease by an equal amount. The commercial bank, on the other hand, gains an asset when it buys the securities, but it loses an asset in the form of a reduction in reserves. If the bank was meeting its reserve requirement previously, then this loss of reserves constitutes a shortfall of reserves for the bank. The bank will be under pressure to contract its lending. As borrowers repay loans, it will not renew them. Its deposit liabilities will then decline, and the M1 money supply falls. This process is also likely to lead to a contraction of lending by other banks and a multiple contraction of bank deposits.
Figure 17.3 shows that the Fed loses securities in the amount of $4,000 and then debits the account of the bank that is paying for the securities. The Fed’s assets and liabilities thus decrease by an equal amount. The commercial bank, on the other hand, gains an asset when it buys the securities, but it loses an asset in the form of a reduction in reserves. If the bank was meeting its reserve requirement previously, then this loss of reserves constitutes a shortfall of reserves for the bank. The bank will be under pressure to contract its lending. As borrowers repay loans, it will not renew them. Its deposit liabilities will then decline, and the M1 money supply falls. This process is also likely to lead to a contraction of lending by other banks and a multiple contraction of bank deposits. As Figure 17.4 shows, the Fed gains a loan asset and credits the bank’s reserve account, which is a liability for the Fed. The bank, on the other hand, acquires a new asset in the form of additional reserves. Because the loan must be repaid, it is a liability for the bank. The additional reserves become excess reserves if the bank was meeting its reserve requirement previously. If it lends the excess reserves, then the lending that it encourages results in the multiple expansion of bank deposits and an increase in the M1 money supply.
As Figure 17.4 shows, the Fed gains a loan asset and credits the bank’s reserve account, which is a liability for the Fed. The bank, on the other hand, acquires a new asset in the form of additional reserves. Because the loan must be repaid, it is a liability for the bank. The additional reserves become excess reserves if the bank was meeting its reserve requirement previously. If it lends the excess reserves, then the lending that it encourages results in the multiple expansion of bank deposits and an increase in the M1 money supply. As Figure 17.5 shows, the Fed will lose a discount loan asset, but its reserve liabilities will fall as the bank repays the loan using reserves. The bank, on the other hand, rids itself of a liability because it no longer owes the Fed for the discount loan, but its reserves fall on the asset side of its balance sheet because it uses reserves to repay the Fed for the loan. If the bank was just meeting its reserve requirement before, it now falls below that legal requirement. The bank will contract its lending as a corrective action. The contraction of bank lending for this one bank triggers a contraction of bank lending throughout the banking system and a reduction in checkable deposits. As a result, the M1 money supply contracts.
As Figure 17.5 shows, the Fed will lose a discount loan asset, but its reserve liabilities will fall as the bank repays the loan using reserves. The bank, on the other hand, rids itself of a liability because it no longer owes the Fed for the discount loan, but its reserves fall on the asset side of its balance sheet because it uses reserves to repay the Fed for the loan. If the bank was just meeting its reserve requirement before, it now falls below that legal requirement. The bank will contract its lending as a corrective action. The contraction of bank lending for this one bank triggers a contraction of bank lending throughout the banking system and a reduction in checkable deposits. As a result, the M1 money supply contracts. As Figure 17.6 shows, the bank has acquired excess reserves of $2,000 due to the reduction in the reserve requirement. Originally, the bank has no excess reserves. As soon as the reserve requirement declines, however, the bank finds itself with excess reserves that it can lend. If it lends the excess reserves, then the bank’s checkable deposits will increase. Therefore, the M1 money supply will rise.
As Figure 17.6 shows, the bank has acquired excess reserves of $2,000 due to the reduction in the reserve requirement. Originally, the bank has no excess reserves. As soon as the reserve requirement declines, however, the bank finds itself with excess reserves that it can lend. If it lends the excess reserves, then the bank’s checkable deposits will increase. Therefore, the M1 money supply will rise.
In the case of an increase in the reserve requirement, the bank finds itself with insufficient reserves. To increase the ratio of bank reserves to deposit liabilities, the bank has several options, but one option is to allow borrowers to repay loans while denying them new loans. As borrowers repay loans, the bank’s checkable deposit liabilities will decline. If the process goes far enough, then the bank’s reserves will provide sufficient backing for the checkable deposits that it has issued. The contraction of checkable deposits will lead to a contraction of lending throughout the banking system and to a multiple contraction of bank deposits. The result is a reduction in the M1 money supply.
We have now seen how the Fed’s three monetary policy tools influence the M1 money supply. The Fed’s monetary policy can be described as either expansionary or contractionary. If the Fed uses its policy tools to increase the money supply, then its monetary policy is described as an expansionary monetary policy or as an easy monetary policy. If, on the other hand, the Fed uses its policy tools to reduce the money supply, then its monetary policy is described as a contractionarymonetary policy or as a tight monetary policy.
T he Neoclassical Approach to Monetary Policy Using an Exogenous Money Supply
Let’s consider how a neoclassical economist analyzes the impact of changes in the money supply on the financial markets and the economy. Consider the case of expansionary monetary policy first. If the Fed acts to expand the M1 money supply, then it must choose one of the three following policy actions:
- Purchase bonds from commercial banks
- Reduce the discount rate
- Lower the reserve requirement ratio
Each of these actions will increase the excess reserves available to commercial banks. Using the excess reserves, banks will increase their lending, which will create more checkable deposits and expand the M1 money supply.
The impact of the Fed’s increase in the money supply is essentially the same as the impact of an increase in the money supply that commercial banks entirely initiate, as described in Chapter 16. Indeed, the Fed is only able to increase the money supply because it encourages banks to lend more. The Fed’s role is different, however, in that it has the legal authority to alter the money supply in a deliberate way and on a massive scale. Each commercial bank, on the other hand, is focused on making a profit and only alters the money supply unintentionally and on a small scale.
The impact on financial markets of the Fed’s monetary expansion is shown in Figure 17.8.

As Figure 17.8 shows, the money supply curve shifts rightward as banks lend more and create more checkable deposits. This shift creates a surplus of money in the money market. That is, firms and households are holding more money than they wish to hold. Consequently, they lend the surplus funds in the loanable funds market, which is equivalent to the purchase of additional bonds in the bond market. In the loanable funds market, the increase in supply creates a surplus of loanable funds. Competition in the loanable funds market drives down the rate of interest to clear that market. Similarly, the higher demand for bonds creates a shortage of bonds in the bond market. Competition in the bond market drives up the price of bonds until the bond market clears. Simultaneous equilibrium thus occurs in all three markets. The Fed’s expansionary monetary policy has pushed interest rates down and bond prices up.[5]
The Fed is primarily interested in promoting increased output and employment as well as a stable price level. If it has made the decision to increase the money supply, then it must believe that the economy is operating at less than full employment. Otherwise, a monetary expansion would be purely inflationary. Figure 17.9 shows the impact of an easy money policy in the case of an economy operating below full employment.

As Figure 17.9 shows, when the supply of money increases, the increased money supply leads to a surplus of money in the money market, which is loaned to borrowers in the loanable funds market. Interest rates fall as described previously. The reduction in interest rates then has an impact on the real economy. The type of aggregate spending that is most sensitive to changes in interest rates is investment spending. When interest rates fall, businesses can obtain loans more cheaply, which they use for the purchase of new capital equipment and new structures (e.g., office buildings, factories, production plants). Home buyers also can obtain mortgage loans more cheaply, which they use to buy new homes. The increase in business investment and residential fixed investment increases aggregate expenditures in the economy causing the A curve to shift upwards in the Keynesian Cross model. The consequence is a rise in the equilibrium level of real GDP.
The level of aggregate demand (AD) also increases. The reader should notice that the rise in AD puts upward pressure on the price level. As the economy approaches full employment, the resulting diminishing returns to labor and the use of less efficient resources pushes unit costs upward, and so firms are forced to raise prices. Therefore, real GDP rises to Y2, which is not quite as much as the increase to Y3. The reason is that the rise in the price level prevents aggregate expenditure from rising quite as much due to the wealth effect, the international substitution effect, and the interest-rate effect described in Chapter 13. In any case, the Fed’s monetary policy has expanded the level of real GDP, but it has also caused some demand-pull inflation.
The impact on investment spending is not the only impact that the Fed’s monetary expansion has on aggregate spending. Figure 17.10 shows a second kind of impact that the Fed’s monetary expansion has on the economy.

In Figure 17.10, we can see that the increase in the money supply puts downward pressure on the rate of interest in the money market as previously described. Foreign investors are likely to be affected when they see that the return on interest-bearing assets in the United States is lower. Specifically, they will be less likely to purchase assets, such as U.S. savings deposits, CDs, and bonds. Because they purchase fewer U.S. interest-bearing assets, they will also purchase fewer U.S. dollars in the foreign exchange market, which are needed to purchase U.S. goods and assets. The reduction in demand for U.S. dollars in the foreign exchange market will cause the foreign exchange value of the U.S. dollar to fall. That is, the U.S. dollar will depreciate.
The depreciation of the U.S. dollar makes U.S. goods relatively cheaper in international commodity markets, which stimulates U.S. exports. The increase in U.S. exports raises aggregate expenditure and boosts real GDP as shown in the Keynesian Cross model. As in the case of a boost to investment spending, the increase in aggregate demand pushes up the price level and prevents real GDP from rising as much as is shown in the Keynesian Cross model. The closer the economy is to full employment, the more the price level will rise and the less the economy will expand in real terms. In general, the Fed’s monetary expansion boosts both investment spending and net export spending, allowing the economy to expand but at the cost of producing some demand-pull inflation.
Now let’s consider the case of contractionary monetary policy. If the Fed acts to reduce the M1 money supply, then it must choose one of the three following policy actions:
- Sell bonds to commercial banks
- Raise the discount rate
- Raise the reserve requirement ratio
Each of these actions will reduce the excess reserves available to commercial banks. With fewer excess reserves, banks will reduce their lending, which will cause a reduction in the amount of checkable deposits and contract the M1 money supply.
The impact of the Fed’s reduction in the money supply is essentially the same as the impact of a decrease in the money supply that commercial banks entirely initiate, as described in Chapter 16. Indeed, the Fed is only able to decrease the money supply because it discourages banks from lending. Again, the Fed’s role is different, however, in that it has the legal authority to reduce the money supply in a deliberate way and on a massive scale. Each commercial bank, on the other hand, is focused on making a profit and only decreases the money supply unintentionally and on a small scale.
The impact on financial markets of the Fed’s monetary contraction is shown in Figure 17.11.

As Figure 17.11 shows, the money supply curve shifts leftward as banks lend less and create fewer checkable deposits. This shift creates a shortage of money in the money market. That is, firms and households are holding less money than they wish to hold. Consequently, they lend fewer funds in the loanable funds market, which is equivalent to the purchase of fewer bonds in the bond market. In the loanable funds market, the reduction in supply creates a shortage of loanable funds. Competition in the loanable funds market drives up the rate of interest to clear that market. Similarly, the lower demand for bonds creates a surplus of bonds in the bond market. Competition in the bond market drives down the price of bonds until the bond market clears. Simultaneous equilibrium thus occurs in all three markets. The Fed’s contractionary monetary policy has pushed interest rates up and bond prices down.
The Fed is primarily interested in promoting increased output and employment as well as a stable price level. If it has made the decision to decrease the money supply, then it must believe that the economy is operating at close to full employment and that inflation is a serious concern. Otherwise, a monetary contraction would worsen an already sluggish economy. Figure 17.12 shows the impact of a tight money policy in the case of an economy operating near full employment.

As Figure 17.12 shows, when the supply of money contracts, the reduced money supply leads to a shortage of money in the money market, which leads to less lending to borrowers in the loanable funds market. Interest rates rise as described previously. The rise in interest rates then has an impact on the real economy. Again, the type of aggregate spending that is most sensitive to changes in interest rates is investment spending. When interest rates rise, businesses must pay more to obtain loans for the purchase of new capital equipment and new structures (e.g., office buildings, factories, production plants). Home buyers must also pay more for mortgage loans, which they use to buy new homes. The reduction in business investment and residential fixed investment decreases aggregate expenditures in the economy causing the A curve to shift downwards in the Keynesian Cross model. The consequence is a drop in the equilibrium level of real GDP.
The level of aggregate demand (AD) also decreases. The reader should notice that the drop in AD puts downward pressure on the price level. If prices are sticky in a downward direction, then the price level will remain stable as the level of output and employment fall. Therefore, real GDP falls to Y2, which is the same reduction in real GDP that occurs in the Keynesian Cross model. The reason that the reduction in real GDP is the same in both the Keynesian Cross and AD/AS models is that the price level is sticky. If the price level does decline, then the wealth effect, the international substitution effect, and the interest-rate effect would cause a movement along the AD curve and partially offset the drop in aggregate spending from the higher interest rates. In any case, the Fed’s monetary policy has reduced the level of real GDP.
It might seem surprising that the Fed would ever pursue a contractionary monetary policy. Indeed, it appears that the Fed is trying to engineer a recession! The Fed might pursue a minor contraction, however, if the economy is approaching full employment and a rise in inflation appears to be a likely result. Fed officials might reason that it is better to weaken the economy a little bit than to allow the boom to create so much inflation that a major monetary contraction is required. The former Federal Reserve Chair, Janet Yellen, argued in 2017 that such a boom-bust policy should be avoided.
The impact on investment spending is not the only impact that the Fed’s monetary contraction has on aggregate spending. Figure 17.13 shows a second kind of impact that the Fed’s monetary contraction has on the economy.

In Figure 17.13, we can see that the decrease in the money supply puts upward pressure on the rate of interest in the money market as previously described. Foreign investors are likely to be affected when they see that the return on interest-bearing assets in the United States is higher. Specifically, they will be more likely to purchase assets, such as U.S. savings deposits, CDs, and bonds. Because they purchase more U.S. interest-bearing assets, they will also purchase more U.S. dollars in the foreign exchange market, which are needed to purchase U.S. goods and assets. The increased demand for U.S. dollars in the foreign exchange market will cause the foreign exchange value of the U.S. dollar to rise. That is, the U.S. dollar will appreciate.
The appreciation of the U.S. dollar makes U.S. goods relatively more expensive in international commodity markets, which reduces U.S. exports. The decrease in U.S. exports lowers aggregate expenditure and reduces real GDP as shown in the Keynesian Cross model. As in the case of a contraction of investment spending, the decrease in aggregate demand puts downward pressure on the price level. If prices are sticky in a downward direction, then the price level will remain stable as the level of output and employment fall. Therefore, real GDP falls to Y2, which is the same reduction in real GDP that occurs in the Keynesian Cross model. As stated previously, the reason that the reduction in real GDP is the same in both the Keynesian Cross and AD/AS models is that the price level is sticky. If the price level does decline, then the wealth effect, the international substitution effect, and the interest-rate effect would cause a movement along the AD curve and partially offset the drop in aggregate spending from the higher interest rates. In any case, the Fed’s monetary policy has reduced the level of real GDP. In general, the Fed’s monetary contraction reduces both investment spending and net export spending, allowing the economy to avoid a surge of inflation but at the cost of some reduction in aggregate output and employment.
The Quantity Theory of Money and the AD/AS Model
Neoclassical economists also defend a theory referred to as the Quantity Theory of Money. It is based on an identity known as the Quantity Equation. The Quantity Equation identifies a specific relationship between the money supply, the velocity of money, the price level, and the level of real output. The velocity of money is the number of times that a unit of the domestic currency (e.g., a U.S. dollar) is spent on average during a given period. For example, if the money velocity is equal to 6, then a dollar bill is spent six times on average during the year. Using this definition of the velocity of money, we can now write the Quantity Equation:
The Quantity Equation shows that the product of the money supply (M) and the velocity of money (V) is equal to the product of the price level (P) and the level of real output (Y). The product of the price level and the level of real output (PY) is the nominal GDP of the economy. Given the velocity of money, M is the money supply that will support that level of nominal spending. For example, suppose that the money supply is $900 billion and the velocity of money is 6. Then if the price level is 2, the level of real output must be $2,700 billion.
The Quantity Equation is just an identity. It is true given the definition of the variables and does not constitute a theory until we consider how the variables in the equation are causally related. Neoclassical economists have traditionally argued that the velocity of money is relatively stable over time. Hence, the quantity of money is the main determinant of the level of nominal GDP. This view suggests that the Fed has a considerable amount of influence over the economy.
As soon as it is argued that an increase in the money supply causes a rise in nominal GDP given a relatively stable money velocity, the Quantity Equation is transformed into a monetary theory called the Quantity Theory of Money. For neoclassical economists, the length of the period under consideration influences the nature of the impact of a money supply change on the economy. For example, in the short run when prices are sticky, a money supply increase (given V) causes an unambiguous rise in the level of real output.
The impact of an increase in the money supply in the short run may be depicted as in Figure 17.14.

Figure 17.14 shows how the rise in the money supply raises aggregate demand and the level of real output while leaving the price level the same. Similarly, a monetary contraction would lower aggregate demand and the level of real output while leaving the price level the same.
In the long run, the situation is reversed. Neoclassical economists argue that the economy will operate at full employment. That is, the quantities of labor, capital, and land will determine the level of real GDP. Therefore, if the money supply rises in the long run (given V), then the price level will rise and the level of real GDP will remain the same.
The impact of an increase in the money supply in the long run may be depicted as in Figure 17.15.
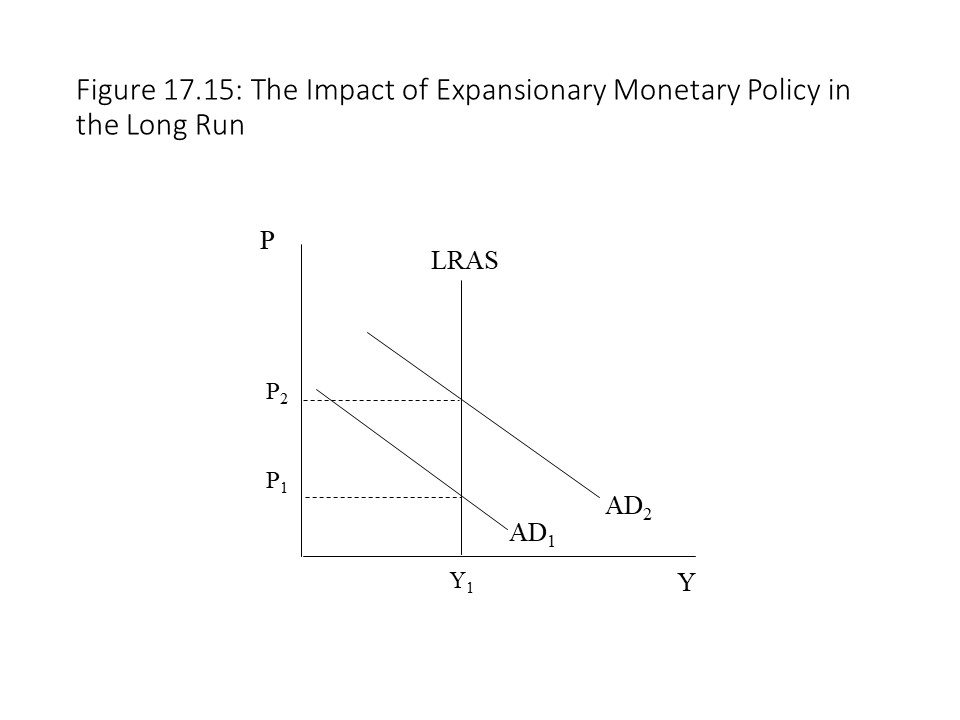 Figure 17.15 shows how the rise in the money supply raises aggregate demand and the price level while leaving the level of real output the same. Similarly, a monetary contraction would lower the price level while leaving the level of real output unchanged.
Figure 17.15 shows how the rise in the money supply raises aggregate demand and the price level while leaving the level of real output the same. Similarly, a monetary contraction would lower the price level while leaving the level of real output unchanged.
The Post-Keynesian Approach to Monetary Policy Using an Endogenous Money Supply
Post-Keynesian economists are critical of the neoclassical approach to monetary policy. Much of the disagreement relates to the assumption that the velocity of money is relatively stable. If the velocity of money is unstable and unpredictable, then changes in the money supply may be offset or intensified when the velocity of money changes. For example, if Fed increases the money supply with the intention of increasing nominal GDP by a given amount, then an unpredictable increase in money velocity may cause an inflationary surge of nominal GDP. On the other hand, if money velocity unpredictably declines, then nominal GDP will not rise as much or may even decline.
Given these questions about the stability and predictability of the velocity of money, it is natural to wonder what the historical evidence suggests. A simple rearrangement of the Quantity Equation allows us to easily calculate the velocity of money.
In other words, if we divide nominal GDP by the money supply, we obtain the velocity of money. Figure 17.16 shows the historical pattern of the M1 velocity of money from 1959 to 2017.

As Figure 17.16 shows, the M1 velocity of money, although increasing steadily, was relatively predictable prior to 1980.[6] This pattern suggests that changes in the money supply could be used to manipulate nominal GDP with a fair amount of accuracy. With sticky prices in the short run, money supply manipulation could be used to influence the level of real GDP, as explained previously. In the long run, however, manipulation of the money supply would alter the price level. In any case, the neoclassical assumption appears to be reasonable prior to 1980.
After 1980, the pattern of money velocity abruptly changes. Money velocity begins to fluctuate in ways that do not appear to follow any predictable pattern. In this environment, altering the money supply with the goal of changing nominal GDP is extremely difficult. Central bankers have no way of knowing how much to change the money supply to alter nominal GDP.
The reasons for the shift are debated. One possibility is that modern information technology has made it easier to transfer funds from non-M1 M2 assets (e.g., savings deposits, MMDAs) to checkable deposits and back again. For example, during the 1990s, we observe a huge jump in the velocity of money. If people began to minimize their M1 money holdings to maximize their interest income from non-M1 M2 assets, then money velocity as defined in this chapter would jump for a given level of nominal GDP. Because it became easier to transfer funds to M1 accounts when they were needed for transactions, many households and firms may have made the decision to hold less M1 money.
Even though the velocity of money began to change in unpredictable ways after 1980, it is worth noting that during recessions since that time (the shaded areas in Figure 17.16), the velocity of money has always fallen. One possibility is that people wish to hold more money during recessions because they are afraid of job loss. The loss of a job means the loss of income and the inability to pay bills. Holding liquid assets during recessions makes sense then. With an increase in currency holdings and checkable deposits (M), the velocity of money (V) will fall. The reduction in velocity will be even greater due to the contraction of nominal GDP (PY) during the recession. A reference to the formula for money velocity provided above confirms these results.
Due to complications that stem from the use of monetary policy, Post-Keynesians tend to share Keynes’s preference for fiscal policy as a means of combatting recessions. The Post-Keynesian objection to neoclassical monetary theory, however, goes beyond the claim that the velocity of money is unstable and unpredictable. Post-Keynesians also argue that the causal relationship between the money supply and the aggregate economy is exactly the reverse of what neoclassical economists assert.
Before exploring the post-Keynesian alternative monetary theory in detail, let’s consider how the neoclassical assertion of an exogenous money supply creates a problem within the AD/AS framework. Suppose that government spending increases in the neoclassical AD/AS model. The result is a rightward shift of the aggregate demand curve as shown in Figure 17.17.
 According to neoclassical theory, this rise in AD causes demand-pull inflation as both real output and the price level increase. The increase in both P and Y suggest that nominal GDP (PY) rises. If the velocity of money is relatively stable, which is the neoclassical assumption, then the only way that a higher price level and higher level of real output can occur is if the money supply increases. It would seem then that the only way for this rightward shift of the AD curve to occur is for the commercial banks to accommodate the increased government spending with increased lending. It is conceivable that the banks could accommodate the increased government spending up to a point, without an injection of reserves from the central bank, if the banks possess sufficient excess reserves and are willing to lend. If they lack sufficient excess reserves, then the central bank must accommodate the federal government’s desire to spend more.
According to neoclassical theory, this rise in AD causes demand-pull inflation as both real output and the price level increase. The increase in both P and Y suggest that nominal GDP (PY) rises. If the velocity of money is relatively stable, which is the neoclassical assumption, then the only way that a higher price level and higher level of real output can occur is if the money supply increases. It would seem then that the only way for this rightward shift of the AD curve to occur is for the commercial banks to accommodate the increased government spending with increased lending. It is conceivable that the banks could accommodate the increased government spending up to a point, without an injection of reserves from the central bank, if the banks possess sufficient excess reserves and are willing to lend. If they lack sufficient excess reserves, then the central bank must accommodate the federal government’s desire to spend more.
As Figure 17.18 shows, the federal government’s assets increase when its Treasury deposits at the Fed increase, but its liabilities also increase because it has issued new debt. This increase in Treasury deposits directly adds to the money supply, and the Fed has monetized the debt. In this way, the money supply increase is endogenously related to government spending. That is, rather than the money supply representing an exogenous variable that changes for reasons not explained in our model, the money supply represents an endogenous variable that changes for reasons explained within our model.
This example shows that the neoclassical commitment to an exogenous money supply makes it difficult to uphold the claim that higher government spending will shift the aggregate demand curve to the right. It is still possible for the government to increase its spending with a constant money supply and money velocity, but only a couple scenarios can explain how such a change occurs. If the government, for example, increases spending, it will increase the production of certain commodities and their prices. With the money supply and money velocity constant, however, a reallocation of spending must occur. That is, spending on other commodities for consumption and investment will decline, causing their production levels and prices to fall. The AD curve does not change since these factors offset one another in the calculation of nominal GDP, and overall PY does not change as shown in Figure 17.19.

Another possibility is that the Fed does not accommodate the government spending increase with a money supply increase, but the reallocation of spending occurs differently. For instance, the increased government spending that pushes up the prices and production of some commodities comes at the expense of spending in input markets. The reduction in spending in input markets could cause the prices of inputs to fall so much that unit costs for firms decline. A reduction in unit production costs shifts the short run aggregate supply (SRAS) curve to the right as explained in Chapter 13. This rightward shift of SRAS puts downward pressure on the price level even though it leads to a higher level of real output. If the fall in the price level is sufficiently large, then it might offset the rise in the prices of government-purchased commodities and the rise in real output. Overall, the economy will expand even though the money supply and velocity of money are constant. This possibility is represented in Figure 17.20.
 The outcome represented in Figure 17.20 is very unlikely to occur. It requires the reallocation of spending to affect the input markets the most. It also requires a very steep AD curve so that the shift of the SRAS curve has a relatively much larger impact on the price level than on the level of real output. In this way, real output can expand even with nominal GDP remaining constant. This case represents a major economic boom without the Fed initiating or even accommodating it. Because this outcome is unlikely to occur, it still makes sense to conclude that a rightward shift of the AD curve is very unlikely to occur following an increase in government spending without some accommodation from the central bank.
The outcome represented in Figure 17.20 is very unlikely to occur. It requires the reallocation of spending to affect the input markets the most. It also requires a very steep AD curve so that the shift of the SRAS curve has a relatively much larger impact on the price level than on the level of real output. In this way, real output can expand even with nominal GDP remaining constant. This case represents a major economic boom without the Fed initiating or even accommodating it. Because this outcome is unlikely to occur, it still makes sense to conclude that a rightward shift of the AD curve is very unlikely to occur following an increase in government spending without some accommodation from the central bank.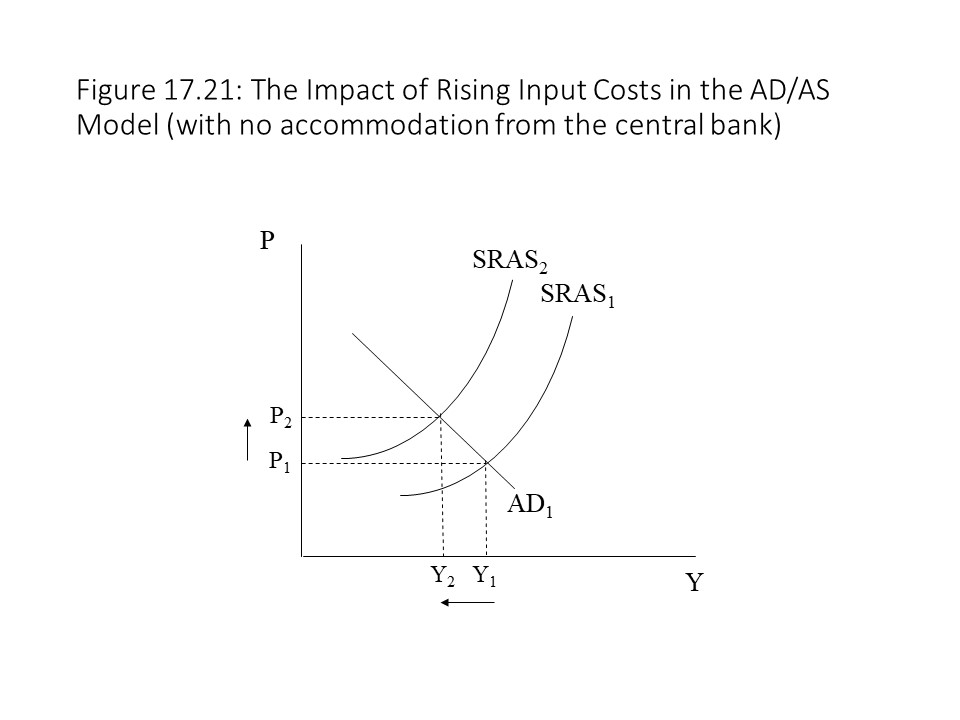 Figure 17.21 shows how a rise in input costs (e.g., wages, oil prices) leads to a leftward shift of the SRAS curve. The result is a rise in the general price level and a reduction in the level of real output. In this case, the fall in real output implies that the rising price level can occur even if the money supply and velocity of money remain constant.
Figure 17.21 shows how a rise in input costs (e.g., wages, oil prices) leads to a leftward shift of the SRAS curve. The result is a rise in the general price level and a reduction in the level of real output. In this case, the fall in real output implies that the rising price level can occur even if the money supply and velocity of money remain constant.
This analysis shows that cost-push inflation does not require accommodation from the banking system and the central bank.
We have seen how the assumption of an exogenous money supply creates problems for the traditional neoclassical analysis of the macroeconomy using the AD/AS model. Let’s take a closer look at why Post-Keynesian economists argue that the supply of money should be treated as an endogenous variable in macroeconomic theory. Post-Keynesian economists typically argue that owners of different factors of production are involved in a conflict over the distribution of income. Workers, for example, demand higher wages and form labor unions to apply pressure on employers. Firms, on the other hand, use their market power to maintain markups of product prices over unit labor costs. A constant struggle ensues that can generate cost-push inflation and a wage-price inflationary spiral. This relationship can be captured best using the following equation:[7]
In the equation above, the price of a product (P) is equal to a markup (m) over the per unit labor cost of production. In this case, the markup is multiplied by the ratio of total labor cost (wL) to total output. Total labor cost is the wage rate (w) times the number of units of labor hired (L). When this total wage bill is spread across the number of units produced (Q), we obtain the labor cost per unit (wL/Q).
When workers demand and win wage increases, firms raise their product prices since they desire a constant markup over unit labor costs. When product prices increase, workers recognize that their real wages (w/P) are eroded, which brings their purchasing power back to the original level. Workers thus demand higher nominal wage increases, which continues the process. One should not assume that workers are the guilty party initiating the wage-price inflationary spiral. Firms might initiate the cycle with an initial increase in the markup over unit labor costs, which raises prices and per unit profits. Workers may then respond with the demand for higher money wages.
The upward pressure on prices means that firms and consumers will have a more difficult time making purchases and will need to obtain more loans to make purchases. They will also need to hold more checkable deposits and currency to engage in desired transactions. Post-Keynesian economists argue that the commercial banks and the central bank will accommodate the desire for additional loans and money balances. That is, the assumption that the money supply is determined endogenously in response to these events carries very different consequences for the financial markets than what we observed when an exogenous money supply was assumed. Figure 17.22 shows the impact on the financial markets of an increased demand for money and loans in the context of an endogenously determined money supply.

Figure 17.22 shows that the rate of interest does not change when the central bank completely accommodates the higher demand for money. As the demand for money rises, the slightest rise in the rate of interest leads to increased commercial bank lending and increased open market purchases by the Fed, which provides banks with more reserves to encourage bank lending. The money supply curve is perfectly elastic as a result. At the same time, the higher demand for loans in the loanable funds market is completely accommodated as the Fed provides banks with more reserves, and the banks lend more. The rise in the supply of loanable funds keeps the rate of interest from rising in the loanable funds market. As the demand for loans rises, the counterpart of this change in the bond market is a higher supply of bonds, which puts downward pressure on bond prices. Because banks accommodate securities dealers’ higher demand for checkable deposits by purchasing their securities, the demand for bonds rises too. This accommodating stance keeps bond prices from falling. Hence, simultaneous equilibrium in all three markets occurs, and interest rates and bond prices remain unchanged.
The constant rate of interest suggests that the cost of borrowing does not change. Hence, aggregate investment spending and consumer spending, which are sensitive to interest rate changes will not change. We should not expect an aggregate demand shift to occur. Even though firms and households are borrowing more, they are doing so in response to a higher price level. It does not represent an increase in the demand for real goods and services. Another way to think about why the AD curve does not shift is to consider the impact on the velocity of money. The higher demand for money has a lower money velocity as its counterpart. Even though the money supply rises, the velocity of money falls, and so AD does not change overall. Nevertheless, the rise in per unit costs does cause a leftward shift of the SRAS curve, and so stagflation results.
Figure 17.23 shows a Post-Keynesian result that involves a wage-price inflationary spiral and recession with accommodation from the Fed and the commercial banks.

In Figure 17.23 the Fed and the banks are accommodating the higher demand for money and loans resulting from the wage-price inflationary spiral. A lending boom takes place within an inflationary economy where output and employment are falling. The lending allows firms and households to continue spending and driving up the price level even as the economy contracts.
The contrast between this Post-Keynesian analysis and the neoclassical analysis should be clear. If the Fed controls the money supply and does not respond to demands of borrowers and banks, then an exogenous money supply increase will push interest rates down and stimulate investment spending and consumer spending. The result will be a rise in aggregate demand and an economic boom capable of producing higher levels of real output and a higher price level as shown in Figure 17.9. The Post-Keynesian analysis, on the other hand, reveals why the monetary expansion of the 1970s was incapable of pulling the economy out of recession even as it produced high rates of inflation.
A Marxian Theory of Fiat Money and its Relationship to U.S. Economic History
In Chapter 4, the Marxian theory of money was developed. In that theory, money serves as the universal expression of socially necessary abstract labor time (SNALT). Each commodity in circulation is equated with the specific quantity of the money commodity that contains the same amount of SNALT. As paper symbols began to circulate as a representative of the money commodity, each commodity acquired a paper money price. Because the paper symbols were convertible into the money commodity (e.g., gold), the paper value of a commodity represented the exact quantity of the money commodity that contained an equivalent amount of SNALT as the commodity. Convertible paper money, therefore, does not present any special challenges for Marxian monetary theory.
As suggested in Chapter 4, the greater challenge to Marxian monetary theory is the existence of inconvertible paper money or fiat money. Because fiat money is not directly convertible into a commodity, it appears that the paper itself possesses value. The problem is that the SNALT required to produce the paper symbols is negligible. Therefore, it does not make sense to compare the labor time required to produce a house with the labor time required to produce $200,000 worth of fiat paper. To make such a comparison would reveal that the labor time required to produce the house far exceeds the labor time required to produce the paper money. The discrepancy seems to suggest that a Marxian theory of fiat money is doomed.
How can we determine the specific quantity of fiat paper for which a commodity will exchange if commodities exchange at their values? Within a system of simple commodity circulation, commodities are constantly being exchanged for money and money is constantly being exchanged for commodities. Commodity circuits with the form C-M-C’ are used to represent these patterns of sale and purchase. The question we are asking is the following: How much money (M) is needed to complete the circuit when the exchange of equivalent values (C for C’) is assumed? In the case of commodity money or convertible paper money, the answer is simple. We just use the amount of commodity money or convertible paper money that represents the same amount of SNALT as the commodities being sold and purchased. That is, a unit of commodity money requires so much SNALT for its production. We simply adjust the quantity of the money commodity so that its value is equivalent to the values of the commodities being exchanged. With fiat paper money, we cannot rely on that solution because, as already argued, the SNALT required for its production is negligible and so it cannot provide the solution if one exists.
The way to resolve the problem is to recognize that fiat paper money continues to represent a claim to other commodities in circulation. Although it cannot be redeemed at a bank for a specific quantity of gold, it can be easily exchanged for commodities. The answer then requires that we reflect on the entire world of circulating commodities. Consider a period during which the circulating paper money supply (M) is given.[8] On average each unit of paper money is spent a specific number of times, which we have called the velocity of money (V). The fiat money price of each commodity represents some fraction of this total expenditure represented as MV. What is the fraction of MV that a specific commodity will command as a price when commodities exchange at their values? It is determined by the SNALT required for its production. Given this reasoning, the fiat money value of a commodity j will equal the following:
In this equation, Lj represents the SNALT required to produce commodity j and ΣLi represents the aggregate SNALT embodied in all n circulating commodities.[9] Pj is the fiat money price or paper value of the commodity j. Only when commodity prices are determined according to this formula will all commodities exchange according to the quantities of SNALT required for their production.
The formula for the fiat money price of commodity j reveals that the paper value of a commodity depends on several factors:
- It depends positively on the SNALT required for its production (Lj). If the SNALT required to produce the commodity rises, then the paper value of the commodity will increase, other factors held constant (and vice versa).
- It depends negatively on the aggregate SNALT embodied in all circulating commodities. Other factors held constant, if the economy expands and more SNALT is required to produce all circulating commodities, then the paper value of the commodity will fall. That is, the commodity represents a smaller fraction of the aggregate labor time embodied in commodities and so it commands a smaller part of the effective money supply (MV). The opposite occurs if the economy contracts.
- It depends positively on the supply of paper money (M). If the money supply rises, other factors held constant, then the fiat paper price of commodity j will increase (and vice versa). In this case, the fraction of the aggregate SNALT devoted to this commodity is applied to a larger effective money supply (MV).
- It depends positively on the velocity of money (V). If the velocity of money increases, then the fiat money price of commodity j will increase (and vice versa). In this case as well, the fraction of the aggregate SNALT devoted to this commodity is applied to a larger effective money supply (MV).
It turns out that this expression for the fiat money price of commodity j is consistent with the Quantity Equation that neoclassical economists describe. To understand the relationship between the fiat money price equation and the Quantity Equation, try adding up all the fiat money prices in the entire economy. Because n commodities are in circulation, we can write the following equation:
This derivation shows that the sum of all prices of circulating commodities is equal to the effective fiat paper money supply. Because some of the prices listed individually in this equation are for the same commodity, we could write the equation using the products of prices and quantities. If we only include prices that are uniquely associated with one commodity and multiply by the quantity in circulation, then we obtain the equation below:
In this equation, Pi‘ refers to the price of commodity i where all the other prices of commodity i have been eliminated to allow for multiplication by the quantity of that commodity in circulation (Yi). In other words, the equation reduces to the Quantity Equation:
Like in neoclassical theory, the Quantity Equation is a simple identity. In Marxian economics, this identity becomes a theory when the prices of the commodities are explained using their individual labor values, the aggregate labor time required for their production, the supply of paper money, and the velocity of money.
The theory provides us with a way of interpreting U.S. macroeconomic history. For example, it is widely recognized that capitalist development has led to an increase in productivity in many sectors of the economy. Increases in productivity allow production to increase more rapidly than production cost. That is, total output per dollar of production cost rises. The flipside of a rise in productivity then is a reduction in production cost per unit of output. In a competitive economy, a reduction in per unit cost should also causes prices to fall as firms compete and profits are pushed down to a level that is consistent with the general rate of profit in the economy. Figures 17.24 and 17.25 show how average labor productivity in the U.S. and the general price level have changed since the 1950s.


As Figure 17.24 shows, the average productivity in the U.S. has risen considerably since 1950. The general price level has also risen as shown in Figure 17.25 for the period 1959-2017. This finding seems to contradict the argument that rising productivity lowers per unit cost and prices in a competitive market economy. How do we resolve this paradox? To resolve the paradox, we need only consider the formula for the price of commodity j. When productivity increases, the SNALT required to produce commodity j falls. Other factors the same, the fiat money price of commodity j will fall. Other factors are not the same, however, because the money supply has grown enormously since 1959 as shown in Figure 17.26.

As the money supply rises, the price of commodity j increases, which shows the inflationary impact of a rise in the money supply. Therefore, the upward pressure on the price due to the increased money supply has offset the downward pressure on the price due to increased productivity. If productivity had not changed at all during this period, then the price of commodity j would have increased even more.
The Marxian theory of fiat money also allows us to respond to a common criticism of Marxian economics. It has been argued that the working class has gained tremendously within capitalist societies as the standard of living has risen. That is, the real wage or the commodity bundle that workers generally consume has increased over time. Because this increase in the real wage has occurred, critics argue, workers are better off, and the suggestion that capitalism would lead to an “increasing misery of the proletariat” is unfounded.[10]
Richard Wolff and Stephen Resnick, however, demonstrate that a rising real wage may occur even as the rate of exploitation rises.[11] To understand their point, suppose that NL represents the necessary labor time expended in the production of commodity j. The reader should recall that necessary labor time refers to the time required to produce a value equivalent to the wage that the worker is paid. The worker must be paid enough for her labor-power to purchase the means of subsistence for the worker and her dependents. If q represents the real wage (expressed in terms of physical units of commodities that workers require for the reproduction of their labor-power), and e represents the SNALT required per unit of commodity in the commodity bundle, then we can write the following equation:
Because the worker requires many different commodities, and each has its own labor requirement, eq represents the product of two vectors or:
In this case, the worker consumes m commodities as part of the required commodity bundle. We can now see how American capitalist development is consistent with a rising rate of exploitation even as the real wage has risen. As productivity has risen, the SNALT required for each commodity in the worker’s commodity bundle has fallen. At the same time, workers have been able to benefit from this increased productivity as the socially acceptable real wage has increased since 1979 as shown in Figure 17.27.

Therefore, each q has increased even as each e has fallen. If the productivity increases (and the corresponding reductions in e) are relatively larger than the increases in the real wage, the necessary labor must fall. Given the length of the working day, the surplus labor thus increases, and the rate of exploitation (S/V or SL/NL) rises, as Wolff and Resnick suggest.
The reader might object, however, to this analysis because a reduction in necessary labor time should mean that the money wage (or nominal wage) has fallen. After all, if it costs less to purchase the commodity bundle due to falling per unit labor values even though the quantities purchased have risen, then less money should be required. U.S. economic history suggests the exact opposite about the overall movement of money wages, which have increased considerably since 1979 as shown in Figure 17.28.

With rising real wages and rising money wages, it seems that Marxian economists cannot defend the claim that workers have been made worse off within capitalist societies. They are not worse off in an absolute sense because of the rise in real wages. They do not appear worse off in a relative sense because of the rise in money wages. The latter suggestion contains a flaw, however, because it ignores the inflationary impact of a rise in the money supply. Looking again at the formula for the price of commodity j, it should be clear that it is possible to multiply any labor time magnitude by the ratio of the effective money supply to the aggregate SNALT embodied in all circulating commodities to obtain a fiat money price. This ratio is a magnitude that Marxian economists refer to as the monetary expression of labor time (MELT):
Hence, the price of commodity j can be written in the following way:[12]
We can use the MELT to calculate the variable capital (v) as follows:
Now consider all the relevant factors that have changed since 1950 in the United States. Productivity has increased, which has caused the real wage to rise and the labor values of commodities to fall. The net change has been a reduction in the necessary labor time because the productivity increases had a relatively larger impact on the labor values than on the real wage. At the same time, the money supply has increased enormously, which has caused the MELT to rise substantially. The variable capital has thus increased, but the increase represents an inflationary increase rather than a redistribution of the new value produced during the workday between capitalists and workers. In other words, the surplus labor (SL) time has increased, reflecting a rise in the rate of exploitation, but the surplus value (S) has also become inflated due to the increase in the MELT.
It should be clear that the surplus value has risen more than the variable capital. Inflation has caused a rise in both measures due to inflation, but the redistribution from the fall in necessary labor time and the rise in surplus labor time has caused the surplus value to rise relatively more than the variable capital has risen.
Before we conclude, it is also helpful to think about the meaning of the reciprocal of the MELT. Its reciprocal is what we might call the value of money (VOM). It shows us how much SNALT is represented with one unit of currency.
Hence, when the MELT rises, the value of money falls. During periods of price inflation, a reduction in the value of money occurs, and so this result is consistent with our intuition.
Monetary Policy Tools within the Context of the Marxian Theory of Financial Markets
In this section, we will consider how a Marxian economist might analyze the Fed’s use of its three primary monetary policy tools. To do so, we will return to the analysis of financial markets that was introduced in Chapter 16. Recall the definition of the general rate of interest (ig) that was provided in that chapter.
It should be immediately apparent that one of the monetary policy tools has already been included in the definition. The reserve requirement ratio (R) was used to determine the amount of excess reserves that a bank can lend. The bank’s total excess reserves are BL+(1-R)D.
Clearly, if the central bank reduces R, then the bank will have more excess reserves that it can lend. This increase in excess reserves will reduce the general rate of interest because a lower interest rate will be sufficient to generate the general rate of profit on bank capital. The reader should recall that the market rate of interest will tend to fall towards the level of the general rate of interest. As soon as the general rate of interest falls below the market rate of interest, capital will flow out of industry and into finance. The increased lending will push the market rate of interest down until it equals the general rate of interest. The conclusion that the market rate of interest will fall when the reserve requirement ratio is reduced is perfectly consistent with the result that neoclassical economists reach. In neoclassical economics, the reduction in the reserve requirement leads to a shift of the money supply curve to the right, which pushes down the market rate of interest in the money market. In Marxian economics, the reduction in the reserve requirement ratio raises the profitability of banking, which leads to capital inflows and pushes down the market rate of interest as lending increases. The results are similar, but these economists reach their conclusions using different theories.
The opposite case involves the central bank increasing the reserve requirement ratio. In this case, the bank will have fewer excess reserves for lending. The general rate of interest will then be higher because a higher interest rate will be needed to ensure the general rate of profit on bank capital. As the general rate of interest rises above the market rate of interest, capital will flow out of finance and into industry. The consequent reduction in bank lending will lead to a higher market rate of interest. The market rate of interest will continue to rise until it equals the general rate of interest. This result is also consistent with the neoclassical conclusion that an increase in the reserve requirement will raise the market rate of interest.
Let’s next consider how open market operations may be incorporated into the Marxian analysis of financial markets. That is, if the central bank buys securities from banks or sells securities to banks, how will that alter the analysis that we have explored thus far? If the central bank is going to be involved in these transactions with commercial banks, then it makes sense to consider how banks acquire securities in the first place.
Consider Table 16.3 that illustrated how the general rate of interest ensures an equal rate of profit in both the industrial sector and the financial sector. In that example, the banks made loans to the industrial capitalists using their excess reserves of $195,000. Industrial capitalists used the borrowed capital of $195,000 to purchase means of production and labor-power. The commodities produced were sold for a profit, and a share of it was given to the bankers in the form of interest.
Now consider how the situation would be different if the bankers sell government bonds to the central bank at the start of this same period. That is, suppose that the central bank decides to purchase government securities in the amount of $97,500 from the commercial banks in an open market purchase. The impact on the central bank’s balance sheet is shown in Figure 17.29.

Figure 17.29 shows that the central bank acquires an asset in the form of government securities and pays the banks for the bonds with an increase in their reserves. Once the central bank takes the securities off the banks’ balance sheets, the banks once again have those excess reserves to lend. In other words, the central bank’s purchase of $97,500 of securities gives the banks new excess reserves, which they can then lend to the industrial capitalists. Table 17.1 shows how the borrowed capital in the industrial sector expands by 1.5 times due to the open market purchase and the additional bank lending that stems from it.

The increase in borrowing in the industrial sector causes the total productive capital in that sector to expand. Consequently, the total profit and the total social product increase. This change reflects the expansionary impact of open market purchases on the economy. At the same time, a lower rate of interest is necessary to ensure the general rate of profit on bank capital since the bank is lending more than previously. In other words, the general rate of interest has fallen:
In this new formula for the general rate of interest, FP represents Federal Reserve open market purchases of securities. These purchases allow the banking system’s excess reserves to increase, which increases lending. Therefore, the rate of interest that is necessary to ensure the general rate of profit on bank capital is lower. Table 17.1 shows that the general rate of interest has fallen to 5.13% (compared with 7.69% prior to the open market purchases). This reduced rate of interest allows the banking sector to appropriate the same amount of interest as before, which ensures a 25% rate of profit. Because the government must also pay interest to the central bank, the interest owed may be calculated as the product of the general rate of interest and the face value of the securities to obtain $5,000 (= 5.13% times $97,500). Industrial capitalists now owe $15,000 in interest payments to the commercial banks due to their expanded borrowing, and the government owes $5,000 in interest payments to the central bank.
This example shows how open market purchases push down the general rate of interest and the market rate of interest while promoting an economic expansion. The process may be reversed if the central bank sells securities it owns to the commercial banks. In that case, FP will decline and the general rate of interest and the market rate of interest will rise. In that case, the banks will lose reserves and will contract their lending.
Finally, let’s consider how central bank discount lending affects the economy and the general rate of interest. In this example, we will assume that the open market purchase described previously has occurred. If the central bank next extends discount loans to commercial banks, then the banks acquire new excess reserves. Assume that the central bank lends $97,500 in discount loans to banks. The banks then grant this entire amount as additional loans to industrial capitalists bringing the total borrowed capital to $390,000. The change to the central bank’s balance sheet, which includes the open market purchase described previously, is shown in Figure 17.30.
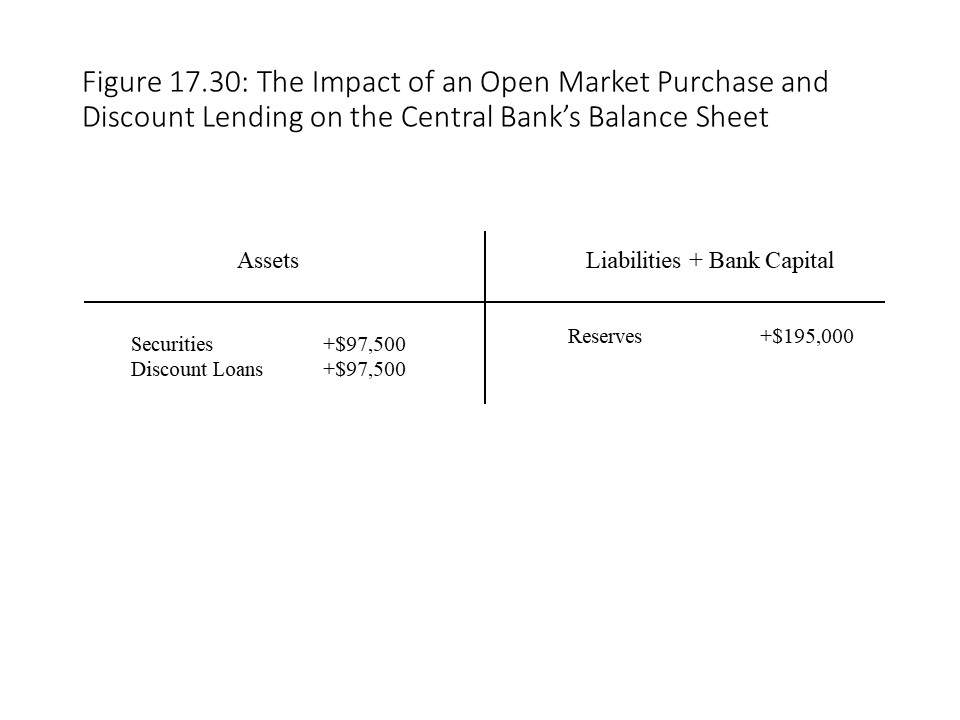 Figure 17.30 shows that the central bank has acquired discount loans as a new asset in addition to the securities previously acquired through the open market purchase of bonds from the banks. The discount loans are granted in the form of reserves, which increases the reserve accounts of banks by $195,000. It is assumed that this entire amount is loaned to the industrial capitalists. The additional $97,500 of discount loans has led to an expansion of the industrial sector by this amount due to increased commercial bank lending stemming from the discount loans. Table 17.2 shows how the borrowed capital expands in the industrial sector when bank lending rises following the granting of the discount loans.
Figure 17.30 shows that the central bank has acquired discount loans as a new asset in addition to the securities previously acquired through the open market purchase of bonds from the banks. The discount loans are granted in the form of reserves, which increases the reserve accounts of banks by $195,000. It is assumed that this entire amount is loaned to the industrial capitalists. The additional $97,500 of discount loans has led to an expansion of the industrial sector by this amount due to increased commercial bank lending stemming from the discount loans. Table 17.2 shows how the borrowed capital expands in the industrial sector when bank lending rises following the granting of the discount loans.

With the expansion of the borrowed capital in the industrial sector, the productive capital and the profit also increase. The total social product also rises. The discount lending has led to an expansion of the economy, which suggests that it is an expansionary monetary policy.
It is also worth considering the impact that the discount lending has on the rate of interest. The general rate changes for two reasons due to the granting of the discount loans as shown below:
First, the extension of discount loans to the banks increases the excess reserves of banks and thus bank lending to the industrial sector. Federal Reserve loans (FL) must, therefore, be added to the aggregate loan amount (or excess reserves) shown in the denominator of the equation. The banks lend reserves they acquire from discount loans and open market purchases by the central bank. They also lend their bank loan capital and the excess reserves they acquire from cash deposits.
Second, the discount loans are not provided at zero cost to the banks. The banks must pay the discount rate (id) for these loans. Therefore, the interest received on loans must be sufficient to cover the interest expense of discount loans. For that reason, idFL is included in the numerator of the equation. This product represents the interest expense of the discount loans. If the commercial banks receive the interest implied in the numerator from the industrial sector, then they will be able to pay the interest expense of the discount loans and their operating expenses and still have enough remaining to equal the average profit.
These changes show how a change in the discount rate affects the general rate of interest and the market rate of interest. When the central bank increases the discount rate, the general rate of interest must rise. The cost of servicing discount loans increases, and the banks must pass this higher cost along to industry if they are to continue to receive the general rate of profit on bank capital. On the other hand, if the central bank reduces the discount rate, then the general rate of interest must fall because the fall in interest expenses allows the banks to earn the general rate of profit on bank capital even as it charges a lower rate of interest on its industrial loans.
Less obvious is the impact that discount lending has on the general rate of interest. Discount loans (FL) are present in the denominator and the numerator. That is, the discount lending leads to more bank lending, which puts downward pressure on the general rate of interest. At the same time, it increases the interest expenses of the bank, which puts upward pressure on the general rate of interest. The question we must answer then is where the increase in discount loans will have the largest relative impact.
To answer this question, it helps to use a bit of calculus. Using the quotient rule from calculus, we can differentiate the general rate of interest with respect to Fed discount loans as follows:
If we set this derivative equal to zero, then we can determine what the discount rate must equal so that discount loans have zero impact on the general rate of interest.
If the fraction is to equal zero, then the numerator must equal zero. In other words:
Now we find the discount rate that solves the equation (id*):
That is, if the discount rate is relatively high (greater than id*), then increased discount lending will raise the general rate of interest due to the high interest expense of the discount loans. On the other hand, if the discount rate is relatively low (lower than id*), then increased discount lending will reduce the general rate of interest due to the low interest expense of the discount loans. Because the discount rate has been historically set at a low level, the impact of discount lending has tended to reduce interest rates, but it is theoretically possible that such lending could increase the general and market rates of interest.
The discount rate shown in Table 17.2 is below the level of the general rate of interest without any discount lending and only open market purchases (id* = 5.13%) as shown in Table 17.1. Therefore, the discount lending causes the general rate of interest to fall to 4.35%.
Table 17.3 shows the case of a relatively high discount rate of 6%.

The discount rate of 6% shown in Table 17.3 is above id*. Therefore, when the discount lending occurs, the interest expense is so great that the general rate of interest rises to 5.35%.
Table 17.4 shows the case of a discount rate that is exactly equal to id*.

When this situation arises, the general rate of interest does not change when the discount lending occurs. The economy expands even as the rate of interest remains the same.
The analysis in this section has explained how interest rates and the scale of economic activity changes when the central bank employs its monetary policy tools. The conclusions resemble those reached in neoclassical economic theory, but they are obtained using a Marxian framework in which industrial capitalists, banking capitalists, and the central bank share in the distribution of profits that the working class produces.
F ollowing the Economic News [13]
According to a recent article in The Wall Street Journal, the Fed committed an error in December 2018 when it reduced the size of its balance sheet and increased interest rates. A reduction in the size of the balance sheet means that the Fed is selling securities, which banks purchase using reserves. Hence, assets (i.e., securities) and liabilities (i.e., reserves) decline, causing a decrease in the size of the Fed’s balance sheet. With reserves declining, the money supply shrinks, which creates a shortage of money in the money market, an increase in borrowing in the loanable funds market, and a rise in the supply of bonds. The consequence is a rise in interest rates and fall in bond prices as our general equilibrium model of the financial markets suggests. The article reports that by July 2019, the Fed was indicating that it would be cutting the federal funds rate by 25 basis points or more, which translates into 0.25% or more. The author of the article explains that the Fed seemed to be acting inconsistently and that much disagreement seems to have arisen among members of the Federal Open Market Committee (FOMC) about the best path forward for monetary policy. The author argues that possible motivations for the rate cut include the slow growth of business investment in the second quarter of 2019 and slowing economic growth among trading partners. A fall in investment and net exports reduces aggregate demand and lowers equilibrium real GDP so the Fed may be hoping to counter these reductions with its rate cut. The author argues that a more likely reason for the rate cut is that the European Central Bank (ECB) indicated its plan to increase its bond purchases, which is an expansionary monetary policy that will push down European interest rates. The likely impact of that change is that investors will purchase U.S. assets, which pay higher interest rates, leading to an appreciation of the U.S. dollar. A dollar appreciation makes U.S. exports more expensive and U.S. imports cheaper. A drop in U.S. net exports is likely to follow, which reduces aggregate demand. Therefore, the Fed’s rate cut would help to discourage an increase in the demand for U.S. assets and U.S. dollars and prevent a dollar appreciation with the accompanying negative impact on net exports.
Summary of Key Points
- Monetary policy refers to the use of money supply changes to influence aggregate production, the aggregate price level, and the level of unemployment.
- The Federal Reserve System consists of a system of 12 Federal Reserve Banks, and the Federal Reserve Board of Governors and the Federal Open Market Committee (FOMC) determine monetary policy.
- The Fed acts as a supervisor of banks, a lender of last resort, an issuer of currency, a banker for commercial banks, a processor of checks, a banker for the federal government, and a regulator of the money supply.
- The Fed influences the money supply using open market purchases and sales of securities, discount lending, and adjustments to the reserve requirement ratio (R).
- Expansionary monetary policy involves monetary expansions and interest rate reductions to boost investment spending and net export spending.
- Contractionary monetary policy involves monetary contractions and interest rate increases to discourage investment spending and net export spending.
- Expansionary monetary policy involves Fed purchases of bonds from banks, discount rate reductions, and reserve requirement ratio reductions.
- Contractionary monetary policy involves Fed sales of bonds to banks, discount rate increases, and reserve requirement ratio increases.
- The Quantity Equation is an identity that shows how the money supply, the velocity of money, the aggregate price level, and the level of real output are all related.
- Whereas the Quantity Theory of Money emphasizes the relative stability and predictability of the velocity of money, Post-Keynesian economists emphasize the instability and unpredictability of money velocity.
- Post-Keynesian economists argue that the class conflict over the distribution of income leads to a wage-price inflationary spiral, which causes banks and the central bank to increase the money supply, thus providing an endogenous explanation for money supply growth.
- The Marxian theory of fiat money treats the price of an individual commodity as a fraction of the effective money supply (MV) where fiat paper money represents a claim to other commodities in circulation.
- Money wages and real wages have risen throughout U.S. economic history due to inflation and productivity growth. Nevertheless, American workers have experienced rising rates of exploitation due to the reduction in the necessary labor time required to produce the consumption bundle that workers consume and the increase in the surplus labor time performed during the workday.
- When the central bank purchases securities from commercial banks, the increased lending to industrial capitalists pushes down the general and market rates of interest and leads to an economic expansion.
- When the central bank increases discount lending to commercial banks, the increased lending to industrial capitalists leads to an economic expansion. It also pushes down the general rate of interest so long as the discount rate is below the zero-impact discount rate.
- When the central bank reduces the discount rate, the general and market rates of interest fall. When the central bank raises the discount rate, the general and market rates of interest rise.
List of Key Terms
Monetary policy
Federal Reserve
Federal Reserve Banks (FRBs)
Federal Reserve Board of Governors
Chair of the Federal Reserve Board
Vice Chair of the Federal Reserve Board
Federal Open Market Committee (FOMC)
Quasi-public institution
Central bank independence
Supervisor of banks
Lender of last resort
Issuer of currency
Federal Reserve Notes
Banker for commercial banks
Processor of checks
Banker for the federal government
Foreign currency-denominated assets
Regulator of the money supply
Open market operations
Discount loans (FL)
Discount rate (id)
Reserve requirement ratio (R)
Expansionary (easy) monetary policy
Contractionary (tight) monetary policy
Boom-bust policy
Quantity Equation
Velocity of money
Quantity Theory of Money
Debt monetization
Exogenous variable
Endogenous variable
Exogenous money supply
Wage-price inflationary spiral
Endogenous money supply
Marxian monetary theory
Marxian theory of fiat money
Effective money supply (MV)
Real wage (q)
Necessary labor (NL)
SNALT required per unit of commodity (e)
Money wage (nominal wage)
Variable capital (v)
Surplus labor (SL)
Value of money (VOM)
Federal Reserve open market purchases of securities (FP)
Zero-impact discount rate (id*)
Problems for Review
- Suppose the Fed purchases $20,000 in bonds from the Valpo Bank. How will the Fed’s balance sheet change? How will the Valpo Bank’s balance sheet change? Show the changes on the Fed’s balance sheet and the Valpo Bank’s balance sheet. What is the impact on the money supply likely to be (e.g., positive, negative)?
- Suppose the Fed sells $30,000 worth of bonds to the Valpo Bank. How will the Fed’s balance sheet change? How will the Valpo Bank’s balance sheet change? Show the changes on the Fed’s balance sheet and the Valpo Bank’s balance sheet. What is the impact on the money supply likely to be (e.g., positive, negative)?
- Suppose the Fed grants a $15,000 discount loan to the Gary Bank. How will the Fed’s balance sheet change? How will the Gary Bank’s balance sheet change? Show the changes on the Fed’s balance sheet and the Valpo Bank’s balance sheet. What is the impact on the money supply likely to be (e.g., positive, negative)?
- Suppose the Gary Bank repays the Fed for a $12,000 discount loan (ignore the interest payment). How will the Fed’s balance sheet change? How will the Gary Bank’s balance sheet change? Show the changes on the Fed’s balance sheet and the Valpo Bank’s balance sheet. What is the impact on the money supply likely to be (e.g., positive, negative)?
- Suppose the Fed reduces the reserve requirement ratio from 15% to 10%. If the South Bend Bank has checkable deposits of $200,000 and $30,000 in reserves, then how is it affected due to the reduction in the required reserve ratio? Show the changes to the South Bend Bank’s balance sheet. What is the impact on the money supply likely to be (e.g., positive, negative)?
- Suppose the Fed raises the reserve requirement ratio from 20% to 25%. If the South Bend Bank has checkable deposits of $200,000 and $40,000 in reserves, then how is it affected due to the increase in the required reserve ratio? Show the changes to the South Bend Bank’s balance sheet. What is the impact on the money supply likely to be (e.g., positive, negative)?
- Suppose the Fed increases the discount rate. According to neoclassical theory, what is expected to happen to bank reserves, the money supply, interest rates, investment spending, the value of the U.S. dollar, and net export spending?
- Suppose the money supply is $2.5 trillion, the velocity of money is 6, and the aggregate price level is 3. What is the level of real output? Use the Quantity Equation.
- Suppose a wage-price deflationary spiral occurs. That is, prices fall and firms insist on cutting workers’ wages. As demand drops, prices fall further. Using Post-Keynesian theory, predict what will happen to money demand, the money supply, interest rates, the supply and demand for loanable funds, the supply and demand for bonds, and bond prices.
- Suppose the SNALT embodied in a mobile phone is 0.5 hours and the aggregate labor time embodied in all circulating commodities is 20 billion hours. If the money supply is $2 trillion and the velocity of money is 5, then what is the fiat money price of the mobile phone?
- Consider Table 17.4. Suppose that the discount rate falls to 0.25%. How is the general rate of interest affected? Carry out the calculation. Compare the 0.25% discount rate to the zero-impact discount rate. Compare the newly calculated general rate of interest to the general rate of interest when no discount lending occurs (i.e., 5.13%). Are your comparisons consistent with your expectations? Explain.
- See Mishkin (2006), p. 339. ↵
- Chisholm and McCarty (1981), p. 207, state that the “purpose is not to earn money but to stabilize American banking and to decide and carry out monetary policy.” ↵
- The monetary policy tools described in this section are discussed in virtually all neoclassical macroeconomics textbooks. ↵
- Mishkin (2006), p. 393-410, provides a helpful model of the supply and demand for bank reserves, which shows how the relationship between the discount rate and the federal funds rate influences the supply curve in the market for bank reserves. ↵
- In this discussion, it is assumed that only one interest rate exists in the economy. Many interest rates exist in the economy, but they tend to move together and so it is useful to refer to only one interest rate. See Mankiw (1997), p. 58, for a discussion of this point. The Fed has the most direct impact on the federal funds rate when it uses its policy tools, which then affects the general structure of interest rates throughout the economy. ↵
- Neoclassical textbooks recognize the increased instability of the M1 money velocity beginning in the early 1980s. For example, see OpenStax College (2014), p. 655. ↵
- A similar equation, based on one that Sidney Weintraub presented, is found in Snowdon, et al. (1994), p. 372. ↵
- Although I refer to the circulating paper money supply throughout this discussion, the symbols may take electronic form and so checkable deposits may also be included here. ↵
- Saros (2002). I prove this result for the case of V = 1 in Saros (2006) and Saros (2007), p. 407-415. Fred Moseley has proven the result for the general case where V is equal to any value, which is a major contribution to Marxian monetary theory. Moseley conclusively proves that Marx's theory of value does not depend on the widespread use of a money commodity such as gold. See Moseley (2004) and Moseley (2011). I was unaware of Moseley's 2004 draft until after the RRPE review process ended for my 2006 submission, which was published in abbreviated form in 2007. I am thankful to Prof. Moseley for recognizing my development of these concepts as "completely independent" of his 2004 draft (see Moseley (2011), p. 102), although the development of my diagrammatic approach was certainly influenced by my reading of the introduction to his edited volume. See Moseley (2005). ↵
- See Hunt (2002), p. 244. Hunt explains that, despite what critics argue, nothing can be found in Marx’s mature writings to suggest that he associated a falling real wage for workers with their increasing misery. ↵
- See Wolff and Resnick (2012), p. 192-195. ↵
- Moseley (2004/2011) has written the equation this way. ↵
- “The Confusing Federal Reserve.” The Wall Street Journal. Eastern edition. New York, NY. 30 July 2019. A.16. ↵


