1.3: Mapping The World
- Page ID
- 38640
Maps are fundamental to the discipline of geography and have been used by humans since before 6,000 B.C. Today’s maps are much more sophisticated, complex, and precise, and are used by many people who employ GPS mapping systems in their vehicles. This technology allows motorists to navigate from place- to-place with relative ease, but the process by which these digital and other maps are created is exceptionally complex.
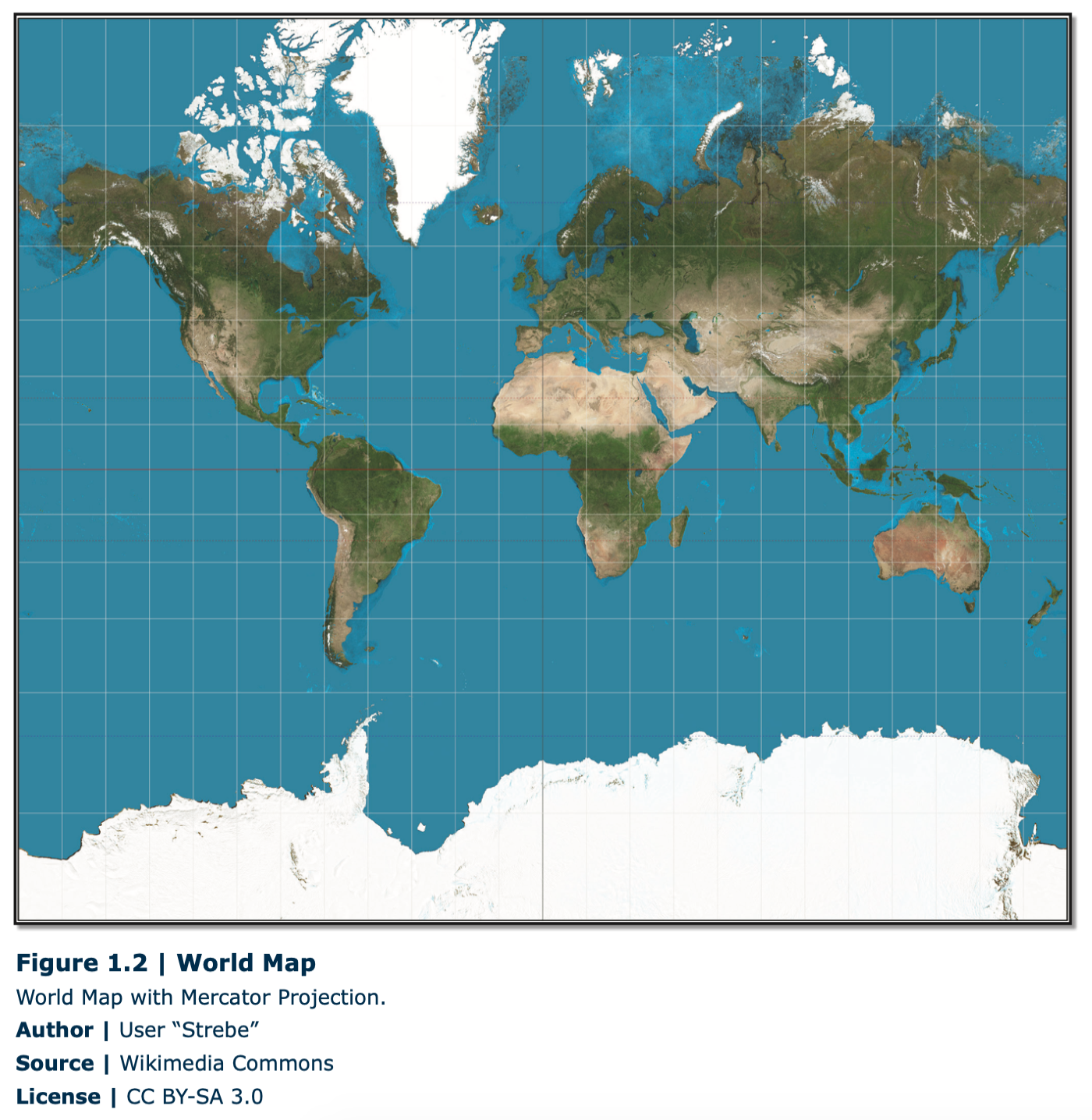
Essentially, a map, which is a flat presentation of a place on Earth, is actually depicting a curved surface. The Earth, which looks like a sphere, is technically an oblate spheroid, which means that the “middle” of the Earth, around the equator, is slightly wider, and the north/south pole axis is slightly shorter, than a perfect sphere. When any curved surface is depicted on a flat surface, that process is known as projection, and many types of map projections exist. A fundamental characteristic of all maps is they involves projections, and all projections have some sort of distortion inherent in them. The size, shape, distance, and direction of objects are distorted to various degrees on maps. The reason this distortion occurs can be visualized by simply imagining peeling an orange, and trying to flatten the peel on a table. If you drew the continents on that orange before peeling it, the continents would most certainly be distorted when you try to flatten the peel on the table. This analogy does not precisely describe how projections are created; the process is much more involved. However, the underlying principle still applies. An example of distortion is shown on the map of the globe below (Figure 1.2). Note, for example, in this Mercator projection that Greenland appears to be larger than South America, although it is, in fact, much smaller.
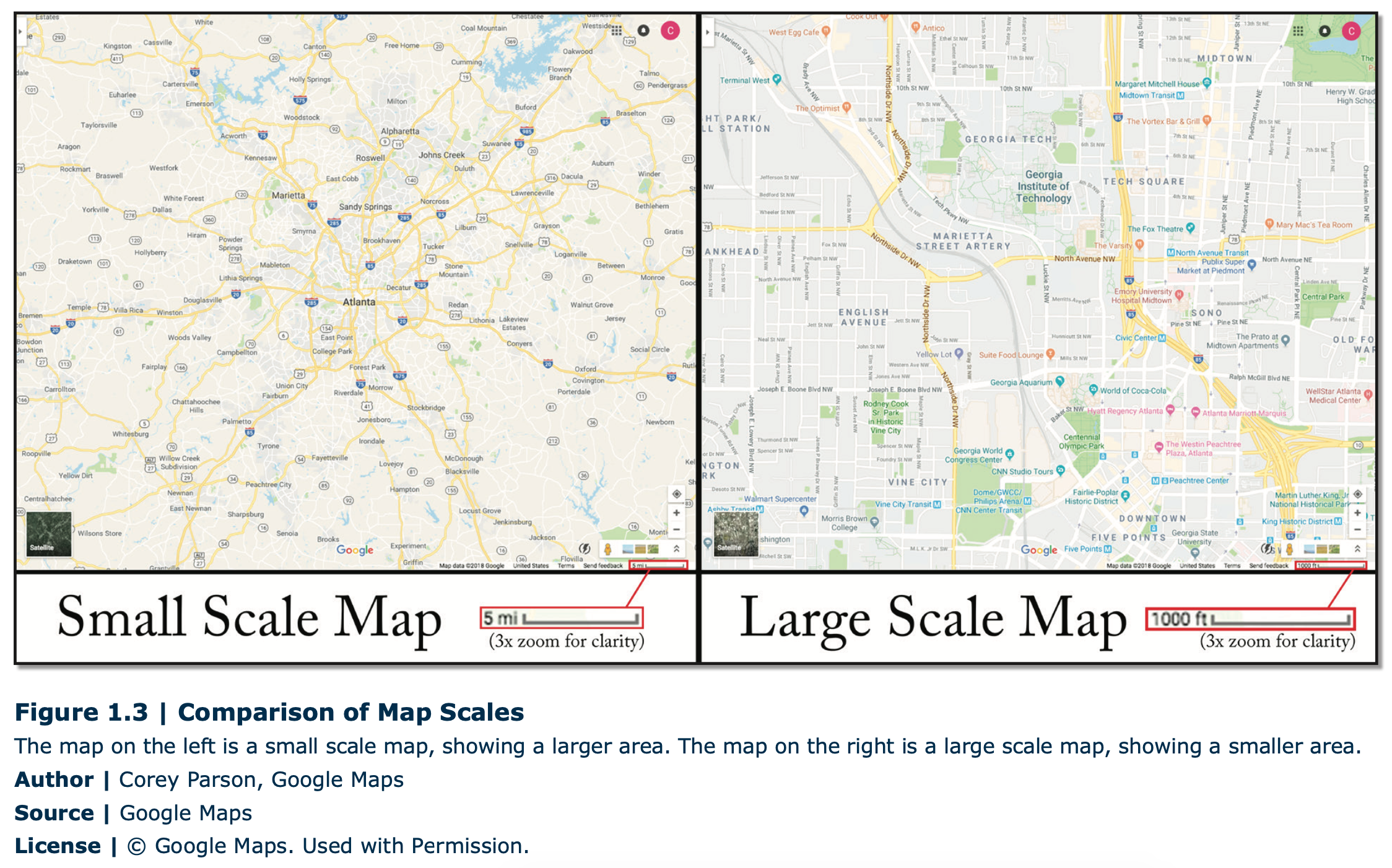
Besides projections, another important characteristic of maps is the scale. The scale of a map is a ratio of the length or distance on the map versus the length or distance on the Earth or ground (actual). The amount of detail shown on a map will vary based on the scale. For example, a map with a scale of 1:100,000 (which means 1 in/cm on the map equals 1,000,000 in/cm on the ground) would show much less detail than a map at a scale of 1:10,000 (Figure 1.3). Besides showing scale as a ratio, it can also be presented as a bar graph or as a verbal statement. Scale can also mean the spatial extent of some kind of phenomena. For example, one could examine migration at the global, national, state, or local scale. By either definition, however, each refers to the level of detail about the place that the geographer is researching. Examining the world from different scales enables different patterns and connections to emerge.