2.4: From the Formal to the Physical

The short story The Dreams in the Witch-house by Lovecraft (1933) explored the link between mathematics and magic. The story explained how a student discovers that the act of writing out mathematical equations can alter reality. This alteration provided an explanation of how the accused Salem witch Keziah Mason escaped her seventeenth-century captors:

She had told Judge Hathorne of lines and curves that could be made to point out directions leading through the walls of space to other spaces and beyond. . . . Then she had drawn those devices on the walls of her cell and vanished. (Lovecraft, 1933, p. 140)

This strange link between the formal and the physical was also central to another paper written in the same era as Lovecraft’s story. The author was Claude Shannon, and the paper’s title was “A symbolic analysis of relay and switching circuits” (Shannon, 1938). However, his was not a work of fiction. Instead, it was a brief version what is now known as one of the most important master’s theses ever written (Goldstine, 1993). It detailed the link between Boolean algebra and electrical circuits, and showed how mathematical logic could be used to design, test, and simplify circuits. “The paper was a landmark in that it helped to change digital circuit design from an art to a science” (p. 120).

Shannon had a lifelong interest in both mathematics and mechanics. While his most influential papers were mathematical in focus (Shannon, 1938, 1948), he was equally famous for his tinkering (Pierce, 1993). His mechanical adeptness led to the invention of a number of famous devices, including Theseus, a mechanical maze-solving mouse. Later in his career Shannon seemed to take more pride in the gadgets that he had created and collected than in his numerous impressive scientific awards (Horgan, 1992).

Shannon’s combined love of the mathematical and the mechanical was evident in his education: he completed a double major in mathematics and electrical engineering at the University of Michigan (Calderbank & Sloane, 2001). In 1936, he was hired as a research assistant at MIT, working with the differential analyzer of Vannevar Bush. This machine was a pioneering analog computer, a complex array of electrical motors, gears, and shafts that filled an entire room. Its invention established Bush as a leader in electrical engineering as well as a pioneer of computing (Zachary, 1997). Bush, like Shannon, was enamored of the link between the formal and the physical. The sight of the differential analyzer at work fascinated Bush “who loved nothing more than to see things work. It was only then that mathematics—his sheer abstractions—came to life” (Zachary, 1997, p. 51).

Because of his work with Bush’s analog computer, Shannon was prepared to bring another mathematical abstraction to life when the opportunity arose. The differential analyzer had to be physically reconfigured for each problem that was presented to it, which in part required configuring circuits that involved more than one hundred electromechanical relays, which were used as switches. In the summer of 1937, Shannon worked in Bell Labs and saw that engineers there were confronted with designing more complex systems that involved thousands of relays. At the time, this was labourious work that was done by hand. Shannon wondered if there was a more efficient approach. He discovered one when he realized that there was a direct mapping between switches and Boolean algebra, which Shannon had been exposed to in his undergraduate studies.

An Internet search will lead to many websites suggesting that Shannon recognized that the opening or closing of a switch could map onto the notions of “false” or “true.” Actually, Shannon’s insight involved the logical properties of combinations of switches. In an interview that originally appeared in Omni magazine in 1987, he noted “It’s not so much that a thing is ‘open’ or ‘closed,’ the ‘yes’ or ‘no’ that you mentioned. The real point is that two things in series are described by the word ‘and’ in logic, so you would say this ‘and’ this, while two things in parallel are described by the word ‘or’” (Liversidge, 1993). In particular, Shannon (1938) viewed a switch (Figure 2-1A) as a source of impedance; when the switch was closed, current could flow and the impedance was 0, but when the switch was open (as illustrated in the figure) the impedance was infinite; Shannon used the symbol 1 to represent this state. As a result, if two switches were connected in series (Figure 2-1B) current would only flow if both switches were closed. Shannon represented this as the sum x + y. In contrast, if switch x and switch y were connected in parallel (Figure 2-1C), then current would flow through the circuit if either (i.e., both) of the switches were closed. Shannon represented this circuit as the product xy. Shannon’s (1938) logical representation is a variation of the two-valued logic that was discussed earlier. The Boolean version of this logic represented false with 0, true with 1, or with addition, and and with multiplication. Shannon’s version represented false with 1, true with 0, or with multiplication, and and with addition. But because Shannon’s reversal of the traditional logic is complete, the two are equivalent. Shannon noted that the basic properties of the two-valued logic were true of his logical interpretation of switches: “Due to this analogy any theorem of the calculus of propositions is also a true theorem if interpreted in terms of relay circuits” (p. 714).

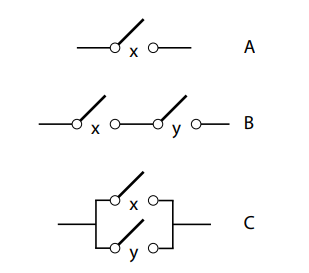
Figure 2-1. (A) An electrical switch, labelled x. (B) Switches x and y in series. (C) Switches x and y in parallel. The practical implication of Shannon’s (1938) paper was that circuit design and testing was no longer restricted to hands-on work in the physical domain. Instead, one could use pencil and paper to manipulate symbols using Boolean logic, designing a circuit that could be proven to generate the desired input-output behaviour. Logical operations could also be used to ensure that the circuit was as simple as possible by eliminating unnecessary logical terms: “The circuit may then be immediately drawn from the equations” (p. 713). Shannon illustrated this technique with examples that included a “selective circuit” that would permit current when 1, 3, or 4—but not 0 or 2—of its relays were closed, as well as an electric combination lock that would only open when its 5 switches were depressed in a specific order. Amazingly, Shannon was not the first to see that electrical circuits were logical in nature (Burks, 1975)! In 1886, Charles Peirce wrote a letter to his student Alan Marquand suggesting how the latter’s logic machine (Marquand, 1885) could be improved by replacing its mechanical components with electrical ones. Peirce provided diagrams of a serial 3-switch circuit that represented logical conjunction (and) and a parallel 3-switch circuit that represented logical disjunction (or). Peirce’s nineteenth-century diagrams would not have been out of place in Shannon’s twentieth-century paper.

In Lovecraft’s (1933) story, the witch Keziah “might have had excellent reasons for living in a room with peculiar angles; for was it not through certain angles that she claimed to have gone outside the boundaries of the world of space we know?” Shannon’s (1938) scholarly paper led to astonishing conclusions for similar reasons: it detailed equivalence between the formal and the physical. It proved that electric circuits could be described in two very different vocabularies: one the physical vocabulary of current, contacts, switches and wires; the other the abstract vocabulary of logical symbols and operations.