3.3: Mechanizing the Infinite

We have seen that the disembodied Cartesian mind is the thinking thing that mediates the sensing of, and acting upon, the world. It does so by engaging in such activities as doubting, understanding, affirming, denying, perceiving, imagining, and willing. These activities were viewed by Descartes as being analogous to a geometer’s use of rules to manipulate mathematical expressions. This leads us to ask, in what medium is thought carried out? What formal rules does it employ? What symbolic expressions does it manipulate?

Many other philosophers were sympathetic to the claim that mental activity was some sort of symbol manipulation. Thomas Hobbes is claimed as one of the philosophical fathers of classical cognitive science because of his writings on the nature of the mind:

When a man Reasoneth, hee does nothing else but conceive a summe totall, from Addition of parcels; or conceive a Remainder, from Substraction of one summe from another.” Such operations were not confined to numbers: “These operations are not incident to Numbers only, but to all manner of things that can be added together, and taken one out of another. (Hobbes, 1967, p. 32)

Hobbes noted that geometricians applied such operations to lines and figures, and that logicians applied these operations to words. Thus it is not surprising that Hobbes described thought as mental discourse—thinking, for him, was language-like.

Why were scholars taken by the idea that language was the medium in which thought was conducted? First, they agreed that thought was exceptionally powerful, in the sense that there were no limits to the creation of ideas. In other words, man in principle was capable of an infinite variety of different thoughts. “Reason is a universal instrument which can operate in all sorts of situations” (Descartes, 2006, p. 47). Second, language was a medium in which thought could be expressed, because it too was capable of infinite variety. Descartes expressed this as follows:

For it is a very remarkable fact that there are no men so dull-witted and stupid, not even madmen, that they are incapable of stringing together different words, and composing them into utterances, through which they let their thoughts be known. (Descartes, 2006, p. 47) Modern linguists describe this as the creative aspect of language (Chomsky, 1965, 1966). “An essential property of language is that it provides the means for expressing indefinitely many thoughts and for reacting appropriately in an indefinite range of new situations” (Chomsky, 1965, p. 6).

While Descartes did not write a great deal about language specifically (Chomsky, 1966), it is clear that he was sympathetic to the notion that language was the medium for thought. This is because he used the creative aspect of language to argue in favor of dualism. Inspired by the automata that were appearing in Europe in his era, Descartes imagined the possibility of having to prove that sophisticated future devices were not human. He anticipated the Turing test (Turing, 1950) by more than three centuries by using language to separate man from machine.

For we can well conceive of a machine made in such a way that it emits words, and even utters them about bodily actions which bring about some corresponding change in its organs . . . but it is not conceivable that it should put these words in different orders to correspond to the meaning of things said in its presence. (Descartes, 2006, p. 46)

Centuries later, similar arguments still appear in philosophy. For instance, why is a phonograph recording of someone’s entire life of speech an inadequate simulation of that speech (Fodor, 1968b)? “At the very best, phonographs do what speakers do, not what speakers can do” (p. 129).

Why might it be impossible for a device to do what speakers can do? For Descartes, language-producing machines were inconceivable because machines were physical and therefore finite. Their finite nature made it impossible for them to be infinitely variable.

Although such machines might do many things as well or even better than any of us, they would inevitably fail to do some others, by which we would discover that they did not act consciously, but only because their organs were disposed in a certain way. (Descartes, 2006, pp. 46–47)

In other words, the creativity of thought or language was only possible in the infinite, nonphysical, disembodied mind.

It is this conclusion of Descartes’ that leads to a marked distinction between Cartesian philosophy and classical cognitive science. Classical cognitive science embraces the creative aspect of language. However, it views such creativity from a materialist, not a dualist, perspective. Developments in logic and in computing that have occurred since the seventeenth century have produced a device that Descartes did not have at his disposal: the physical symbol system. And—seemingly magically—a physical symbol system is a finite artifact that is capable of an infinite variety of behaviour.

By the nineteenth century, the notion of language as a finite system that could be infinitely expressive was well established (Humboldt, 1999, p. 91): “For language is quite peculiarly confronted by an unending and truly boundless domain, the essence of all that can be thought. It must therefore make infinite employment of finite means.” While Humboldt’s theory of language has been argued to presage many of the key properties of modern generative grammars (Chomsky, 1966), it failed to provide a specific answer to the foundational question that it raised: how can a finite system produce the infinite? The answer to that question required advances in logic and mathematics that came after Humboldt, and which in turn were later brought to life by digital computers.

While it had been suspected for centuries that all traditional pure mathematics can be derived from the basic properties of natural numbers, confirmation of this suspicion was only obtained with advances that occurred in the nineteenth and twentieth centuries (Russell, 1993). The “arithmetisation” of mathematics was established in the nineteenth century, in what are called the Dedekind-Peano axioms (Dedekind, 1901; Peano, 1973). This mathematical theory defines three primitive notions: 0, number, and successor. It also defines five basic propositions: 0 is a number; the successor of any number is a number; no two numbers have the same successor; 0 is not the successor of any number; and the principle of mathematical induction. These basic ideas were sufficient to generate the entire theory of natural numbers (Russell, 1993).

Of particular interest to us is the procedure that is used in this system to generate the set of natural numbers. The set begins with 0. The next number is 1, which can be defined as the successor of 0, as s(0). The next number is 2, which is the successor of 1, s(1), and is also the successor of the successor of 0, s(s(0)). In other words, the successor function can be used to create the entire set of natural numbers: 0, s(0), s(s(0)), s(s(s(0))), and so on.

The definition of natural numbers using the successor function is an example of simple recursion; a function is recursive when it operates by referring to itself. The expression s(s(0)) is recursive because the first successor function takes as input another version of itself. Recursion is one method by which a finite system (such as the Dedekind-Peano axioms) can produce infinite variety, as in the set of natural numbers.

Recursion is not limited to the abstract world of mathematics, nor is its only role to generate infinite variety. It can work in the opposite direction, transforming the large and complex into the small and simple. For instance, recursion can be used to solve a complex problem by reducing it to a simple version of itself. This problem-solving approach is often called divide and conquer (Knuth, 1997).

One example of this is the famous Tower of Hanoi problem (see Figure 3-1), first presented to the world as a wooden puzzle by French mathematician Edouard Lucas in 1883. In this puzzle, there are three locations, A, B, and C. At the start of this problem there is a set of differently sized wooden discs stacked upon one another at location A. Let us number these discs 0, 1, 2, and so on, where the number assigned to a disc indicates its size. The goal for the problem is to move this entire stack to location C, under two restrictions: first, only one disc can be moved at a time; second, a larger disc can never be placed upon a smaller disc.

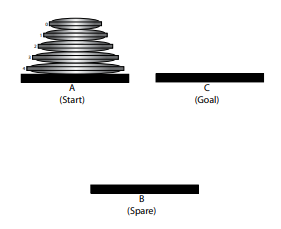
Figure 3-1. The starting configuration for a five-disc version of the Tower of Hanoi problem.

The simplest version of the Tower of Hanoi problem starts with only disc 0 at location A. Its solution is completely straightforward: disc 0 is moved directly to location C, and the problem is solved. The problem is only slightly more complicated if it starts with two discs stacked on location A. First, disc 0 is moved to location B. Second, disc 1 is moved to location C. Third, disc 0 is moved from A to C, stacked on top of disc 1, and the problem has been solved.

What about a Tower of Hanoi problem that begins with three discs? To solve this more complicated problem, we can first define a simpler subproblem: stacking discs 0 and 1 on location B. This is accomplished by doing the actions defined in the preceding paragraph, with the exception that the goal location is B for the subproblem. Once this subtask is accomplished, disc 2 can be moved directly to the final goal, location C. Now, we solve the problem by moving discs 0 and 1, which are stacked on B, to location C, by again using a procedure like the one described in the preceding paragraph.

This account of solving a more complex version of the Tower of Hanoi problem points to the recursive nature of divide and conquer: we solve the bigger problem by 0 1 2 3 4 A (Start) B (Spare) C (Goal) first solving a smaller version of the same kind of problem. To move a stack of n discs to location C, we first move the smaller stack of n – 1 discs to location B. “Moving the stack” is the same kind of procedure for the n discs and for the n – 1 discs. The whole approach is recursive in the sense that to move the big stack, the same procedure must first be used to move the smaller stack on top of the largest disc.

The recursive nature of the solution to the Tower of Hanoi is made obvious if we write a pseudocode algorithm for moving the disks. Let us call our procedure MoveStack (). It will take four arguments: the number of discs in the stack to be moved, the starting location, the “spare” location, and the goal location. So, if we had a stack of three discs at location A, and wanted to move the stack to location C using location B as the spare, we would execute MoveStack (3, A, B, C).

The complete definition of the procedure is as follows:

MoveStack (N, Start, Spare, Goal)

If N = 0

Exit

Else

MoveStack (N – 1, Start, Goal, Spare)

MoveStack (1, Start, Spare, Goal)

MoveStack (N – 1, Spare, Start, Goal)

EndIf

Note the explicit recursion in this procedure, because MoveStack () calls itself to move a smaller stack of disks stacked on top of the disk that it is going to move. Note too that the recursive nature of this program means that it is flexible enough to work with any value of N. Figure 3-2 illustrates an intermediate state that occurs when this procedure is applied to a five-disc version of the problem.

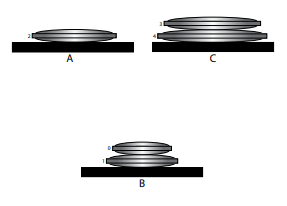
Figure 3-2. An intermediate state that occurs when MoveStack () is applied to a five-disc version of the Tower of Hanoi.

In the code given above, recursion was evident because MoveStack () called itself. There are other ways in which recursion can make itself evident. For instance, recursion can produce hierarchical, self-similar structures such as fractals (Mandelbrot, 1983), whose recursive nature is immediately evident through visual inspection. Consider the Sierpinski triangle (Mandelbrot, 1983), which begins as an equilateral triangle (Figure 3-3).

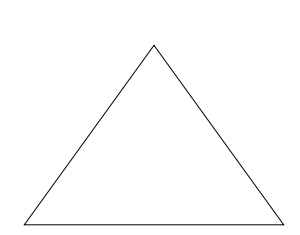
Figure 3-3. The root of the Sierpinski triangle is an equilateral triangle.

The next step in creating the Sierpinski triangle is to take Figure 3-3 and reduce it to exactly half of its original size. Three of these smaller triangles can be inscribed inside of the original triangle, as is illustrated in Figure 3-4.

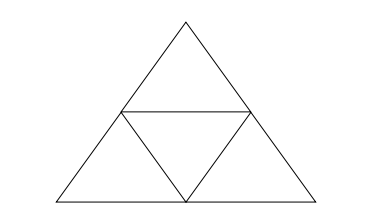
Figure 3-4. The second step of constructing a Sierpinski triangle.

The rule used to create Figure 3-4 can be applied recursively and (in principle) infinitely. One takes the smaller triangle that was used to create Figure 3-4, makes it exactly half of its original size, and inscribes three copies of this still smaller triangle into each of the three triangles that were used to create Figure 3-4. This rule can be applied recursively to inscribe smaller triangles into any of the triangles that were added to the figure in a previous stage of drawing. Figure 3-5 shows the result when this rule is applied four times to Figure 3-4.

Figure 3-5. The Sierpinski triangle that results when the recursive rule is applied four times to Figure 3-4.

The Sierpinski triangle, and all other fractals that are created by recursion, are intrinsically self-similar. That is, if one were to take one of the smaller triangles from which Figure 3-4 is constructed and magnify it, one would see still see the hierarchical structure that is illustrated above. The structure of the whole is identical to the (smaller) structure of the parts. In the next section, we see that the recursive nature of human language reveals itself in the same way.