3.5: Behaviourism, Language, and Recursion
- Page ID
- 21218
Behaviourism viewed language as merely being observable behaviour whose development and elicitation was controlled by external stimuli:
A speaker possesses a verbal repertoire in the sense that responses of various forms appear in his behavior from time to time in relation to identifiable conditions. A repertoire, as a collection of verbal operants, describes the potential behavior of a speaker. To ask where a verbal operant is when a response is not in the course of being emitted is like asking where one’s knee-jerk is when the physician is not tapping the patellar tendon. (Skinner, 1957, p. 21)
Skinner’s (1957) treatment of language as verbal behaviour explicitly rejected the Cartesian notion that language expressed ideas or meanings. To Skinner, explanations of language that appealed to such unobservable internal states were necessarily unscientific:
It is the function of an explanatory fiction to allay curiosity and to bring inquiry to an end. The doctrine of ideas has had this effect by appearing to assign important problems of verbal behavior to a psychology of ideas. The problems have then seemed to pass beyond the range of the techniques of the student of language, or to have become too obscure to make further study profitable. (Skinner, 1957, p. 7)
Modern linguistics has explicitly rejected the behaviourist approach, arguing that behaviourism cannot account for the rich regularities that govern language (Chomsky, 1959b).
The composition and production of an utterance is not strictly a matter of stringing together a sequence of responses under the control of outside stimulation and intraverbal association, and that the syntactic organization of an utterance is not something directly represented in any simple way in the physical structure of the utterance itself. (Chomsky, 1959b, p. 55)
Modern linguistics has advanced beyond behaviourist theories of verbal behaviour by adopting a particularly technical form of logicism. Linguists assume that verbal behaviour is the result of sophisticated symbol manipulation: an internal generative grammar.
By a generative grammar I mean simply a system of rules that in some explicit and well-defined way assigns structural descriptions to sentences. Obviously, every speaker of a language has mastered and internalized a generative grammar that expresses his knowledge of his language. (Chomsky, 1965, p. 8)
A sentence’s structural description is represented by using a phrase marker, which is a hierarchically organized symbol structure that can be created by a recursive set of rules called a context-free grammar. In a generative grammar another kind of rule, called a transformation, is used to convert one phrase marker into another.
The recursive grammars that have been developed in linguistics serve two purposes. First, they formalize key structural aspects of human languages, such as the embedding of clauses within sentences. Second, they explain how finite resources are capable of producing an infinite variety of potential expressions. This latter accomplishment represents a modern rebuttal to dualism; we have seen that Descartes (1996) used the creative aspect of language to argue for the separate, nonphysical existence of the mind. For Descartes, machines were not capable of generating language because of their finite nature.
Interestingly, a present-day version of Descartes’ (1996) analysis of the limitations of machines is available. It recognizes that a number of different information processing devices exists that vary in complexity, and it asks which of these devices are capable of accommodating modern, recursive grammars. The answer to this question provides additional evidence against behaviourist or associationist theories of language (Bever, Fodor, & Garrett, 1968).
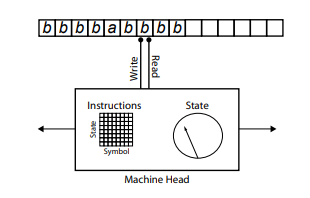
Figure 3-8. How a Turing machine processes its tape.
In Chapter 2, we were introduced to one simple—but very powerful—device, the Turing machine (Figure 3-8). It consists of a machine head that manipulates the symbols on a ticker tape, where the ticker tape is divided into cells, and each cell is capable of holding only one symbol at a time. The machine head can move back and forth along the tape, one cell at a time. As it moves it can read the symbol on the current cell, which can cause the machine head to change its physical state. It is also capable of writing a new symbol on the tape. The behaviour of the machine head—its new physical state, the direction it moves, the symbol that it writes—is controlled by a machine table that depends only upon the current symbol being read and the current state of the device. One uses a Turing machine by writing a question on its tape, and setting the machine head into action. When the machine head halts, the Turing machine’s answer to the question has been written on the tape.
What is meant by the claim that different information processing devices are available? It means that systems that are different from Turing machines must also exist. One such alternative to a Turing machine is called a finite state automaton (Minsky, 1972; Parkes, 2002), which is illustrated in Figure 3-9. Like a Turing machine, a finite state automaton can be described as a machine head that interacts with a ticker tape. There are two key differences between a finite state machine and a Turing machine.
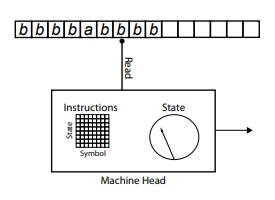
Figure 3-9. How a finite state automaton processes the tape. Note the differences between Figures 3-9 and 3-8.
First, a finite state machine can only move in one direction along the tape, again one cell at a time. Second, a finite state machine can only read the symbols on the tape; it does not write new ones. The symbols that it encounters, in combination with the current physical state of the device, determine the new physical state of the device. Again, a question is written on the tape, and the finite state automaton is started. When it reaches the end of the question, the final physical state of the finite state automaton represents its answer to the original question on the tape.
It is obvious that a finite state automaton is a simpler device than a Turing machine, because it cannot change the ticker tape, and because it can only move in one direction along the tape. However, finite state machines are important information processors. Many of the behaviours in behaviour-based robotics are produced using finite state machines (Brooks, 1989, 1999, 2002). It has also been argued that such devices are all that is required to formalize behaviourist or associationist accounts of behaviour (Bever, Fodor, & Garrett., 1968).
What is meant by the claim that an information processing device can “accommodate” a grammar? In the formal analysis of the capabilities of information processors (Gold, 1967), there are two answers to this question. Assume that knowledge of some grammar has been built into a device’s machine head. One could then ask whether the device is capable of accepting a grammar. In this case, the “question” on the tape would be an expression, and the task of the information processor would be to accept the string, if it is grammatical according to the device’s grammar, or to reject the expression, if it does not belong to the grammar. Another question to ask would be whether the information processor is capable of generating the grammar. That is, given a grammatical expression, can the device use its existing grammar to replicate the expression (Wexler & Culicover, 1980)?
In Chapter 2, it was argued that one level of investigation to be conducted by cognitive science was computational. At the computational level of analysis, one uses formal methods to investigate the kinds of information processing problems a device is solving. When one uses formal methods to determine whether some device is capable of accepting or generating some grammar of interest, one is conducting an investigation at the computational level.
One famous example of such a computational analysis was provided by Bever, Fodor, and Garrett (1968). They asked whether a finite state automaton was capable of accepting expressions that were constructed from a particular artificial grammar. Expressions constructed from this grammar were built from only two symbols, a and b. Grammatical strings in the sentence were “mirror images,” because the pattern used to generate expressions was bNabN where N is the number of bs in the string. Valid expressions generated from this grammar include a, bbbbabbbb, and bbabb. Expressions that cannot be generated from the grammar include ab, babb, bb, and bbbabb.
While this artificial grammar is very simple, it has one important property: it is recursive. That is, a simple context-free grammar can be defined to generate its potential expressions. This context-free grammar consists of two rules, where Rule 1 is S → a, and Rule 2 is a → bab. A string is begun by using Rule 1 to generate an a. Rule 2 can then be applied to generate the string bab. If Rule 2 is applied recursively to the central bab then longer expressions will be produced that will always be consistent with the pattern bNabN.
Bever, Fodor, and Garrett (1968) proved that a finite state automaton was not capable of accepting strings generated from this recursive grammar. This is because a finite state machine can only move in one direction along the tape, and cannot write to the tape. If it starts at the first symbol of a string, then it is not capable of keeping track of the number of bs read before the a, and comparing this to the number of bs read after the a. Because it can’t go backwards along the tape, it can’t deal with recursive languages that have embedded clausal structure.
Bever, Fodor, and Garrett (1968) used this result to conclude that associationism (and radical behaviourism) was not powerful enough to deal with the embedded clauses of natural human language. As a result, they argued that associationism should be abandoned as a theory of mind. The impact of this proof is measured by the lengthy responses to this argument by associationist memory researchers (Anderson & Bower, 1973; Paivio, 1986). We return to the implications of this argument when we discuss connectionist cognitive science in Chapter 4.
While finite state automata cannot accept the recursive grammar used by Bever, Fodor, and Garrett (1968), Turing machines can (Révész, 1983). Their ability to move in both directions along the tape provides them with a memory that enables them to match the number of leading bs in a string with the number of trailing bs.
Modern linguistics has concluded that the structure of human language must be described by grammars that are recursive. Finite state automata are not powerfulenough devices to accommodate grammars of this nature, but Turing machines are. This suggests that an information processing architecture that is sufficiently rich to explain human cognition must have the same power—must be able to answer the same set of questions—as do Turing machines. This is the essence of the physical symbol system hypothesis (Newell, 1980), which are discussed in more detail below. The Turing machine, as we saw in Chapter 2 and further discuss below, is a universal machine, and classical cognitive science hypothesizes that “this notion of symbol system will prove adequate to all of the symbolic activity this physical universe of ours can exhibit, and in particular all the symbolic activities of the human mind” (Newell, 1980, p. 155).


