9.2: Bond Prices, Yields and Interest Rates
- Page ID
- 11838
Before we can discuss the demand for money that comes from portfolio decisions, we need to understand the relationship between interest rates, bond coupons, the prices of financial assets, and yields on financial assets. To keep our discussion simple, we will assume only one type of financial asset, a bond. However, the prices and yields of other financial assets are related to interest rates in the same way as bond prices.
Several concepts are important for our discussion. A bond is an asset that makes one or more fixed money payments to its holder each year until its maturity date. On its maturity date, it also repays its principal value.
Bond: a financial contract that makes one or more fixed money payments at specific dates in the future.
The interest rate [is] the current market rate, expressed as a percentage, paid to lenders or charged to borrowers.
Interest rate: the current market rate paid to lenders or charged to borrowers.
A bond coupon is the fixed money payment made annually to the holders of the bond from the date of issue until the date of maturity. The coupon rate is a fixed percentage of the principal value of the bond at the time of issue.
Bond coupon: the annual fixed money payment paid to a bond holder.
The price of a marketable bond is the current price at which it can be bought or sold on the open bond market at any time between its date of issue and its maturity date.
Price of a marketable bond: the current price at which the bond trades in the bond market.
The yield on a bond is the return to a bond holder expressed as an annual percentage rate, which is a combination of the coupon payments and any change in the market price of the bond during the period in which it is held.
Yield on a bond: the return to a bond holder expressed as an annual percentage.
The ongoing and continuous purchases and sales of bonds on the bond market establish the equilibrium prices of bonds. At those prices, the yields on the bonds at that point in time are equal to the market rate of interest. Changes in bond prices with changing bond market conditions change yields and market interest rates. In late 2008, for example, uncertainty in financial markets led portfolio managers to shift to low-risk assets like Government of Canada bonds. This increased demand for bonds bid bond prices up, and yields on Government of Canada 1-to-3 year bonds fell from 3.22 percent in January 2008 to 1.11 percent in December 2008. In the same period, yields on 3-to-5 year bonds fell from 3.45 percent to 1.61 percent.
With slow recoveries from the recession that followed the 2008-09 financial crisis monetary policy shifted to low interest rates to provide economic stimulus. These low policy rates, slow economic growth continue in 2014 and the effects have spread across terms to maturity in the bond market. As of late April 2014 Government of Canada benchmark bond yields were: 3 year 1.21 percent, 5 year 1.71 percent and 10 year 2.45 percent.
Consider an example that shows the relationship between bond coupons, current market interest rates, bond prices, and yields. Suppose one such bond is listed as:
Government of Canada 4.250 June 1, 2017
This is a marketable 4.25 percent bond with a maturity date of June 1, 2017. It promises to pay its holder $4.25 for each $100 of face value on June 1 each year until June 1, 2017. The $4.25 is the coupon value and $100 is the principal value. On June 1, 2017, the bond matures and pays $104.25, the coupon plus the principal.
Bond prices depend on current market interest rates. The current price of a bond is the present value of the future payments it will provide. Present value is the discounted value of those future payments. It recognizes that money payments in the future are worth less than money payments today. To help understand present value, ask the following question: If someone offers to give you $1000, would you rather have it today or a year from today?
Bond price: the present value of future payments of interest and principal.
Present value is the discounted value of future payments.
Notice that $1000 lent at an interest rate of 3 percent would give you a sum of:
\($1,000 \times (1.03) = $1,030\)
one year from today. In the same way, the amount of money you need to lend today to have $1000 one year from today is:
\(\begin{align}
$M \times (1.03) &= $1,000 \notag\\
$M &= \frac{$1,000}{(1.03)} \notag\\
$M &= $970.87 \notag
\end{align}\)
When the market rate of interest is 3 percent, the present value of $1000 to be received one year in the future is $970.87.
By experimenting with different interest rate assumptions in this present value calculation you will see that the present value of $1,000 to be paid one year from today changes with the rate of interest. Higher interest rates reduce present values while lower rates increase them.
This relationship is the key to understanding bond prices and how they fluctuate over time. A rise in market interest rates lowers the prices of outstanding bonds. A fall in market rates increases bond prices. Bond prices and interest rates move inversely. A couple of examples illustrate this relationship.
First consider the price of the 4.25 percent bond described above. Let’s assume that the 3 year market rate of interest on the date you buy the bond, say June 1, 2014 is 4.25 percent. The price of the bond is the present value of the future payments: $4.25 on June 1, 2015, $4.25 on June 1, 2016, and $104.25 on June 1, 2017. Payments to be received two years in the future are discounted twice, and three years in the future three times, to give:
\(\begin{align}
PV &= \frac{$4.25}{(1.0425)} + \frac{$4.25}{(1.0425)^2} + \frac{$104.25}{(1.0425)^3} \notag\\
PV &= $4.076 + $3.911 + $92.013 \notag\\
PV &= $100.00 \notag
\end{align}\)
If you paid $100 for each $100 of face value and held the bond to maturity, it would yield 4.25 percent, the current market rate of interest assumed in this example. We would say the bond is trading at par because the market price equals the face value.
As an alternative example let’s assume that the 3 year market rate of interest on your purchase date June 1, 2014 is 1.75 percent, which is closer to current rates. The price of the bond is then the present value of the future payments: $4.25 on June 1, 2015, $4.25 on June 1, 2016, and $104.25 on June 1, 2017. Payments to be received two years in the future are discounted twice, and three years in the future three times, to give:
\(\begin{align}
PV &= \frac{$4.25}{(1.0175)} + \frac{$4.25}{(1.0175)^2} + \frac{$104.25}{(1.0175)^3} \notag\\
PV &= $4.177 + $4.125 + $98.962 \notag\\
PV &= $107.26 \notag
\end{align}\)
The price of this 4.25 percent bond on June 1, 2014 would be $107.26 per $100 of face value. The assumption that the market rate of interest is 1.75 percent, which is clearly lower than the 4.25 percent coupon on the bond, means the bond trades at a premium. The premium price means that buying the bond and holding it to its maturity date will give you an annualized return of 1.75 percent on your money. That is the assumed 3 year rate.
In this case the yield on the bond—the present value of its coupon payment plus the capital loss as its price falls to par at maturity—gives a rate of return equal to the market interest rate of 1.75 percent.
Yield on a bond: the coupon plus any capital gain or loss from the change in price between the date of purchase and the date of maturity
In general, because the future payments offered by bonds are fixed in dollar terms, the prices of marketable bonds vary inversely to market rates of interest. Rising interest rates mean falling bond prices, and falling interest rates mean rising bond prices. There are many types of bonds that differ by coupon, maturity date, frequency of future payments, and in other ways. However, the relationship between prices, yields, and interest rates remains the same. Because bond prices are the present value of future payments, prices and interest rates move in opposite directions.
Furthermore, the size of the change in the price of a bond as a result of a change in the interest rate depends on the bond’s term to maturity. The prices of longer-term bonds are more volatile than those of shorter-term bonds. This an important consideration for bond portfolio managers concerned with trade-offs between risk and return. To see this, rework the numerical example where the term to maturity is one year rather than three.
Bond markets in action
Asset markets like the bond market are very active. Large volumes of bonds are bought and sold every business day. If portfolio managers see bond prices that offer yields higher than current market interest rates, they buy bonds. Buying makes prices rise and yields fall until yields and current interest rates are equal. Conversely, if bondholders find yields are lower than interest rates, they sell bonds, bond prices fall, and yields rise. Table 9.1 provides a sample of the information on bond prices and yields. The first three columns define the bond. The next two give current prices and yields.
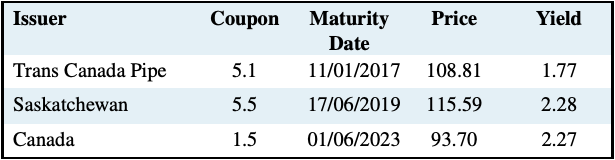
Table 9.1: Bond prices and yields, April 16, 2014
A Trans Canada Pipe 5.10 percent coupon is the first listed in Table 9.1. It matures on the 11th day of January 2017, about 32 months from the date of this quotation. The price is what sellers or buyers were willing to accept or pay for some of these outstanding bonds. The final column reports the yield to maturity from buying this bond in April 2014 and holding it until January 2017. These yields also reflect the market rate of interest for 32-month money on April 16, 2014, which is 1.77 percent.
The first two bonds reported in the table are trading at a premium. Their market prices exceed $100 for $100 of principal value, and their yields to maturity are lower than their coupons. The third bond is trading at a discount. The coupons paid by the bonds reflect market interest rates at the time the bonds were issued. Three and five year market interest rates at those times were higher than on April 2014. The borrowers had to offer higher coupons to sell bonds in the market conditions at the time of issue. The ten market year rate was lower than the April 2014 ten year market rate when the 1.5% coupon Canada was issued. Consequently, it traded at a discount in April 2016.
The fall in Canadian interest rates over the past few years has been good for bondholders. As our calculation of bond prices tells us, falling interest rates raise bond prices. Bondholders enjoyed capital gains as the prices of their bonds rose, in addition to the interest income their bonds paid. We see these higher bond prices in the table.
Of course, market conditions can change. If interest rates were to rise from the 2012 levels, bond prices would fall. Bondholders would suffer capital losses as interest rates rose and bond prices fell. This is the market risk that comes with holding bonds and other marketable financial assets.
Bonds are only one of the alternatives to money in a wealth portfolio. Application Box 9.1 describes some other assets, their prices and yields, in a bit more detail. To understand the demand for money balances and the operation of financial markets, we need to know how these financial assets, which are alternatives to money balances, differ from money. The choice to hold money balances, regardless of motive, is a choice between money and other forms in which wealth could be held.
There are three broad classes of financial assets that are bought and sold in financial markets. These are bills, bonds, and equities.
Bills are short-term financial assets that make no interest payment to the holder but do make specified cash payment on their maturity date. They trade at a discount. A government treasury bill or T-Bill is an example. Every second week the government sells T-Bills that promise to pay the buyer $100 for each $100 of face value on the date that is about three months in the future. The interest earned is the difference between the price paid and the face amount received at the maturity date.
Bonds are longer-term financial assets that pay a fixed money income payment each year and repay their face value on a fixed maturity date. Bonds are marketable, and trade on the bond market between their issue dates and maturity dates at prices determined by supply and demand. As with T-Bills, the return to the holder of a bond depends on the price paid for the bond. In this case, the calculation is more complex however, because it involves a fixed annual money payment and a fixed value at maturity.
Equities are shares in the ownership of the business. They give the holder the right to a share in the profits of the business, either in the form of dividend payments or in terms of the increase in the size of the business if profits are used for business expansion. The shares or stocks in publicly traded businesses can be bought and sold on stock markets like the Toronto Stock Exchange. The financial pages of major newspapers give you daily reports on stocks prices and stock markets. ShareholdersâA˘Z returns from their stock holdings depend ´ on the combination of dividend income they receive and the changes in the market price of the shares they hold. Equity prices are the expected value of the future profits of business. Because expectations of future business performance are volatile, equity prices are volatile and therefore risky. Equities do however offer the prospect of higher long-term returns.
Application Box 9.1: A basic guide to financial assets


