7.4: Entry and Exit Decisions in the Long Run
- Last updated
- Save as PDF
- Page ID
- 51360
Learning Objectives
- Explain how entry and exit lead to zero profits in the long run
- Discuss the long-run adjustment process
The line between the short run and the long run cannot be defined precisely with a stopwatch, or even with a calendar. It varies according to the specific business. The distinction between the short run and the long run is therefore more technical: in the short run, firms cannot change the usage of fixed inputs, while in the long run, the firm can adjust all factors of production.
In a competitive market, profits are a red cape that incites businesses to charge. If a business is making a profit in the short run, it has an incentive to expand existing factories or to build new ones. New firms may start production, as well. When new firms enter the industry in response to increased industry profits it is called entry.
Losses are the black thundercloud that causes businesses to flee. If a business is making losses in the short run, it will either keep limping along or just shut down, depending on whether its revenues are covering its variable costs. But in the long run, firms that are facing losses will shut down at least some of their output, and some firms will cease production altogether. The long-run process of reducing production in response to a sustained pattern of losses is called exit. The following Clear It Up feature discusses where some of these losses might come from, and the reasons why some firms go out of business.
Example \(\PageIndex{1}\): Why do firms cease to exist?
Can we say anything about what causes a firm to exit an industry? Profits are the measurement that determines whether a business stays operating or not. Individuals start businesses with the purpose of making profits. They invest their money, time, effort, and many other resources to produce and sell something that they hope will give them something in return. Unfortunately, not all businesses are successful, and many new startups soon realize that their “business adventure” must eventually end.
In the model of perfectly competitive firms, those that consistently cannot make money will “exit,” which is a nice, bloodless word for a more painful process. When a business fails, after all, workers lose their jobs, investors lose their money, and owners and managers can lose their dreams. Many businesses fail. The U.S. Small Business Administration indicates that in 2011, \(409,040\) new firms "entered," and \(470,376\) firms failed.
Sometimes a business fails because of poor management or workers who are not very productive, or because of tough domestic or foreign competition. Businesses also fail from a variety of causes that might best be summarized as bad luck. For example, conditions of demand and supply in the market shift in an unexpected way, so that the prices that can be charged for outputs fall or the prices that need to be paid for inputs rise. With millions of businesses in the U.S. economy, even a small fraction of them failing will affect many people—and business failures can be very hard on the workers and managers directly involved. But from the standpoint of the overall economic system, business exits are sometimes a necessary evil if a market-oriented system is going to offer a flexible mechanism for satisfying customers, keeping costs low, and inventing new products.
How Entry and Exit Lead to Zero Profits in the Long Run
No perfectly competitive firm acting alone can affect the market price. However, the combination of many firms entering or exiting the market will affect overall supply in the market. In turn, a shift in supply for the market as a whole will affect the market price. Entry and exit to and from the market are the driving forces behind a process that, in the long run, pushes the price down to minimum average total costs so that all firms are earning a zero profit.
To understand how short-run profits for a perfectly competitive firm will evaporate in the long run, imagine the following situation. The market is in long-run equilibrium, where all firms earn zero economic profits producing the output level where \(P = MR = MC\) and \(P = AC\). No firm has the incentive to enter or leave the market. Let’s say that the product’s demand increases, and with that, the market price goes up. The existing firms in the industry are now facing a higher price than before, so they will increase production to the new output level where \(P = MR = MC\).
This will temporarily make the market price rise above the average cost curve, and therefore, the existing firms in the market will now be earning economic profits. However, these economic profits attract other firms to enter the market. Entry of many new firms causes the market supply curve to shift to the right. As the supply curve shifts to the right, the market price starts decreasing, and with that, economic profits fall for new and existing firms. As long as there are still profits in the market, entry will continue to shift supply to the right. This will stop whenever the market price is driven down to the zero-profit level, where no firm is earning economic profits.
Short-run losses will fade away by reversing this process. Say that the market is in long-run equilibrium. This time, instead, demand decreases, and with that, the market price starts falling. The existing firms in the industry are now facing a lower price than before, and as it will be below the average cost curve, they will now be making economic losses. Some firms will continue producing where the new \(P = MR = MC\), as long as they are able to cover their average variable costs. Some firms will have to shut down immediately as they will not be able to cover their average variable costs, and will then only incur their fixed costs, minimizing their losses. Exit of many firms causes the market supply curve to shift to the left. As the supply curve shifts to the left, the market price starts rising, and economic losses start to be lower. This process ends whenever the market price rises to the zero-profit level, where the existing firms are no longer losing money and are at zero profits again. Thus, while a perfectly competitive firm can earn profits in the short run, in the long run the process of entry will push down prices until they reach the zero-profit level. Conversely, while a perfectly competitive firm may earn losses in the short run, firms will not continually lose money. In the long run, firms making losses are able to escape from their fixed costs, and their exit from the market will push the price back up to the zero-profit level. In the long run, this process of entry and exit will drive the price in perfectly competitive markets to the zero-profit point at the bottom of the \(AC\) curve, where marginal cost crosses average cost.
The Long-Run Adjustment and Industry Types
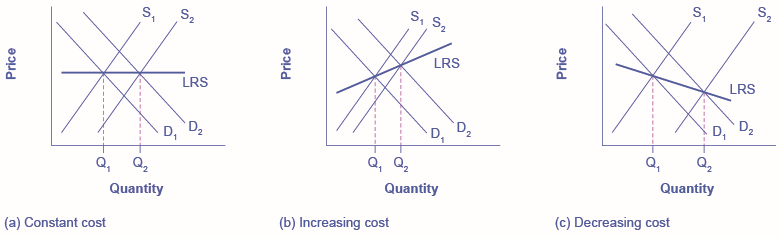
Whenever there are expansions in an industry, costs of production for the existing and new firms could either stay the same, increase, or even decrease. Therefore, we can categorize an industry as being (1) a constant cost industry (as demand increases, the cost of production for firms stays the same), (2) an increasing cost industry (as demand increases, the cost of production for firms increases), or (3) a decreasing cost industry (as demand increases the costs of production for the firms decreases).
For a constant cost industry, whenever there is an increase in market demand and price, then the supply curve shifts to the right with new firms’ entry and stops at the point where the new long-run equilibrium intersects at the same market price as before. But why will costs remain the same? In this type of industry, the supply curve is very elastic. Firms can easily supply any quantity that consumers demand. In addition, there is a perfectly elastic supply of inputs—firms can easily increase their demand for employees, for example, with no increase to wages. Tying in to our Bring it Home discussion, an increased demand for ethanol in recent years has caused the demand for corn to increase. Consequently, many farmers switched from growing wheat to growing corn. Agricultural markets are generally good examples of constant cost industries.
For an increasing cost industry, as the market expands, the old and new firms experience increases in their costs of production, which makes the new zero-profit level intersect at a higher price than before. Here companies may have to deal with limited inputs, such as skilled labor. As the demand for these workers rise, wages rise and this increases the cost of production for all firms. The industry supply curve in this type of industry is more inelastic.
For a decreasing cost industry, as the market expands, the old and new firms experience lower costs of production, which makes the new zero-profit level intersect at a lower price than before. In this case, the industry and all the firms in it are experiencing falling average total costs. This can be due to an improvement in technology in the entire industry or an increase in the education of employees. High tech industries may be a good example of a decreasing cost market.
Figure \(\PageIndex{1}\) (a) presents the case of an adjustment process in a constant cost industry. Whenever there are output expansions in this type of industry, the long-run outcome implies more output produced at exactly the same original price. Note that supply was able to increase to meet the increased demand. When we join the before and after long-run equilibriums, the resulting line is the long run supply (LRS) curve in perfectly competitive markets. In this case, it is a flat curve. Figure \(\PageIndex{1}\) (b) and Figure \(\PageIndex{1}\) (c) present the cases for an increasing cost and decreasing cost industry, respectively. For an increasing cost industry, the LRS is upward sloping, while for a decreasing cost industry, the LRS is downward sloping.
Adjustment Process in a Constant-Cost Industry
Key Concepts and Summary
In the long run, firms will respond to profits through a process of entry, where existing firms expand output and new firms enter the market. Conversely, firms will react to losses in the long run through a process of exit, in which existing firms reduce output or cease production altogether. Through the process of entry in response to profits and exit in response to losses, the price level in a perfectly competitive market will move toward the zero-profit point, where the marginal cost curve crosses the AC curve, at the minimum of the average cost curve.
The long-run supply curve shows the long-run output supplied by firms in three different types of industries: constant cost, increasing cost, and decreasing cost.
Glossary
- entry
- the long-run process of firms entering an industry in response to industry profits
- exit
- the long-run process of firms reducing production and shutting down in response to industry losses
- long-run equilibrium
- where all firms earn zero economic profits producing the output level where \(P = MR = MC\) and \(P = AC\)


