9.3: Oligopoly
- Last updated
- Save as PDF
- Page ID
- 51371
Skills to Develop
- Explain why and how oligopolies exist
- Contrast collusion and competition
- Interpret and analyze the prisoner’s dilemma diagram
- Evaluate the tradeoffs of imperfect competition
Many purchases that individuals make at the retail level are produced in markets that are neither perfectly competitive, monopolies, nor monopolistically competitive. Rather, they are oligopolies. Oligopoly arises when a small number of large firms have all or most of the sales in an industry. Examples of oligopoly abound and include the auto industry, cable television, and commercial air travel. Oligopolistic firms are like cats in a bag. They can either scratch each other to pieces or cuddle up and get comfortable with one another. If oligopolists compete hard, they may end up acting very much like perfect competitors, driving down costs and leading to zero profits for all. If oligopolists collude with each other, they may effectively act like a monopoly and succeed in pushing up prices and earning consistently high levels of profit. Oligopolies are typically characterized by mutual interdependence where various decisions such as output, price, advertising, and so on, depend on the decisions of the other firm(s). Analyzing the choices of oligopolistic firms about pricing and quantity produced involves considering the pros and cons of competition versus collusion at a given point in time.
Why Do Oligopolies Exist?
A combination of the barriers to entry that create monopolies and the product differentiation that characterizes monopolistic competition can create the setting for an oligopoly. For example, when a government grants a patent for an invention to one firm, it may create a monopoly. When the government grants patents to, for example, three different pharmaceutical companies that each has its own drug for reducing high blood pressure, those three firms may become an oligopoly.
Similarly, a natural monopoly will arise when the quantity demanded in a market is only large enough for a single firm to operate at the minimum of the long-run average cost curve. In such a setting, the market has room for only one firm, because no smaller firm can operate at a low enough average cost to compete, and no larger firm could sell what it produced given the quantity demanded in the market.
Quantity demanded in the market may also be two or three times the quantity needed to produce at the minimum of the average cost curve—which means that the market would have room for only two or three oligopoly firms (and they need not produce differentiated products). Again, smaller firms would have higher average costs and be unable to compete, while additional large firms would produce such a high quantity that they would not be able to sell it at a profitable price. This combination of economies of scale and market demand creates the barrier to entry, which led to the Boeing-Airbus oligopoly for large passenger aircraft.
The product differentiation at the heart of monopolistic competition can also play a role in creating oligopoly. For example, firms may need to reach a certain minimum size before they are able to spend enough on advertising and marketing to create a recognizable brand name. The problem in competing with, say, Coca-Cola or Pepsi is not that producing fizzy drinks is technologically difficult, but rather that creating a brand name and marketing effort to equal Coke or Pepsi is an enormous task.
Collusion or Competition?
When oligopoly firms in a certain market decide what quantity to produce and what price to charge, they face a temptation to act as if they were a monopoly. By acting together, oligopolistic firms can hold down industry output, charge a higher price, and divide up the profit among themselves. When firms act together in this way to reduce output and keep prices high, it is called collusion. A group of firms that have a formal agreement to collude to produce the monopoly output and sell at the monopoly price is called a cartel. However, one major issue facing oligopolies is trusting each other, as we will see below.
See the following Clear It Up feature for a more in-depth analysis of the difference between the two.
Collusion versus cartels: How can I tell which is which?
In the United States, as well as many other countries, it is illegal for firms to collude since collusion is anti-competitive behavior, which is a violation of antitrust law. Both the Antitrust Division of the Justice Department and the Federal Trade Commission have responsibilities for preventing collusion in the United States.
The problem of enforcement is finding hard evidence of collusion. Cartels are formal agreements to collude. Because cartel agreements provide evidence of collusion, they are rare in the United States. Instead, most collusion is tacit, where firms implicitly reach an understanding that competition is bad for profits.
The desire of businesses to avoid competing so that they can instead raise the prices that they charge and earn higher profits has been well understood by economists. Adam Smith wrote in Wealth of Nations in 1776: “People of the same trade seldom meet together, even for merriment and diversion, but the conversation ends in a conspiracy against the public, or in some contrivance to raise prices.”
Even when oligopolists recognize that they would benefit as a group by acting like a monopoly, each individual oligopoly faces a private temptation to produce just a slightly higher quantity and earn slightly higher profit—while still counting on the other oligopolists to hold down their production and keep prices high. If at least some oligopolists give in to this temptation and start producing more, then the market price will fall. Indeed, a small handful of oligopoly firms may end up competing so fiercely that they all end up earning zero economic profits—as if they were perfect competitors. Trust is Key!
Game Theory
Game theory is the science of strategic decision-making or strategic-interaction in situations that involve more than one actor. These can include actual games, or real-life situations like military battles, business interactions, or managerial decisions. According to game theory, the best strategy for an individual may or may not be the same depending on the stakes of the game and given the likely move of the other player involved.
Sometimes, the best strategy will be the same no matter how other players act. This is known as the dominant strategy. A dominant strategy is the best strategy for an individual player regardless of the moves of any other player. An example would be if you are playing Poker. In this case, the only hand that a player could have that would be a dominant strategy would be a Royal Flush. An Ace-high, Royal Flush is the only hand that beats every other hand, no other player can have this hand. Thus, the player will win every time and they should bet!
On the other hand, there exists the so-called Nash equilibrium, which does not describe a particular strategy per se, but rather a sort of mutual understanding-- each player understands the other player's optimal strategies and takes those into consideration when optimizing her own strategy.
- According to game theory, the dominant strategy is the optimal move for an individual regardless of how other players act.
- A Nash equilibrium describes the optimal state of the game where both players make optimal moves but now consider the moves of their opponent.
- A well-known example of where the Nash equilibrium plays out in game theory is the prisoner's dilemma.
The Prisoner’s Dilemma
Because of the complexity of oligopoly, which is the result of mutual interdependence among firms, there is no single, generally-accepted theory of how oligopolies behave, in the same way that we have theories for all the other market structures. Instead, economists use game theory, a branch of mathematics that analyzes situations in which players must make decisions and then receive payoffs based on what other players decide to do. Game theory has found widespread applications in the social sciences, as well as in business, law, and military strategy.
The prisoner’s dilemma is a scenario in which the gains from cooperation are larger than the rewards from pursuing self-interest. It applies well to oligopoly. The story behind the prisoner’s dilemma goes like this:
Two co-conspiratorial criminals are arrested. When they are taken to the police station, they refuse to say anything and are put in separate interrogation rooms. Eventually, a police officer enters the room where Prisoner A is being held and says: “You know what? Your partner in the other room is confessing. So your partner is going to get a light prison sentence of just one year, and because you’re remaining silent, the judge is going to stick you with eight years in prison. Why don’t you get smart? If you confess, too, we’ll cut your jail time down to five years, and your partner will get five years, also.” Over in the next room, another police officer is giving exactly the same speech to Prisoner B. What the police officers do not say is that if both prisoners remain silent, the evidence against them is not especially strong, and the prisoners will end up with only two years in jail each.
The game theory situation facing the two prisoners is shown in Table \(\PageIndex{1}\). To understand the dilemma, first consider the choices from Prisoner A’s point of view. If A believes that B will confess, then A ought to confess, too, so as to not get stuck with the eight years in prison. But if A believes that B will not confess, then A will be tempted to act selfishly and confess, so as to serve only one year. The key point is that A has an incentive to confess regardless of what choice B makes! B faces the same set of choices, and thus will have an incentive to confess regardless of what choice A makes. Confess is considered the dominant strategy or the strategy an individual (or firm) will pursue regardless of the other individual’s (or firm’s) decision. The result is that if prisoners pursue their own self-interest, both are likely to confess, and end up doing a total of \(10\) years of jail time between them.
Table \(\PageIndex{1}\): The Prisoner’s Dilemma Problem
| Prisoner B | |||
| Remain Silent (cooperate with other prisoner) | Confess (do not cooperate with other prisoner) | ||
| Prisoner A | Remain Silent (cooperate with other prisoner) | A gets 2 years, B gets 2 years | A gets 8 years, B gets 1 year |
| Confess (do not cooperate with other prisoner) | A gets 1 year, B gets 8 years | A gets 5 years B gets 5 years | |
The game is called a dilemma because if the two prisoners had cooperated by both remaining silent, they would only have had to serve a total of four years of jail time between them. If the two prisoners can work out some way of cooperating so that neither one will confess, they will both be better off than if they each follow their own individual self-interest, which in this case leads straight into longer jail terms.
The Oligopoly Version of the Prisoner’s Dilemma (Duopoly-or Two Oligopolists)
The members of an oligopoly can face a prisoner’s dilemma, also. If each of the oligopolists cooperates in holding down output, then high monopoly profits are possible. Each oligopolist, however, must worry that while it is holding down output, other firms are taking advantage of the high price by raising output and earning higher profits. Table \(\PageIndex{2}\) shows the prisoner’s dilemma for a two-firm oligopoly—known as a duopoly. If Firms A and B both agree to hold down output, they are acting together as a monopoly and will each earn \(\$1,000\) in profits. However, both firms’ dominant strategy is to increase output, in which case each will earn \(\$400\) in profits.
Table \(\PageIndex{2}\): A Prisoner’s Dilemma for Oligopolists
| Firm B | |||
| Hold Down Output (cooperate with other firm) | Increase Output (do not cooperate with other firm) | ||
| Firm A | Hold Down Output (cooperate with other firm) | A gets $1,000, B gets $1,000 | A gets $200, B gets $1,500 |
| Increase Output (do not cooperate with other firm) | A gets $1,500, B gets $200 | A gets $400, B gets $400 | |
Can the two firms trust each other? Consider the situation of Firm A:
- If A thinks that B will cheat on their agreement and increase output, then A will increase output, too, because for A the profit of \(\$400\) when both firms increase output (the bottom right-hand choice in Table \(\PageIndex{2}\)) is better than a profit of only \(\$200\) if A keeps output low and B raises output (the upper right-hand choice in the table).
- If A thinks that B will cooperate by holding down output, then A may seize the opportunity to earn higher profits by raising output. After all, if B is going to hold down output, then A can earn \(\$1,500\) in profits by expanding output (the bottom left-hand choice in the table) compared with only \(\$1,000\) by holding down output as well (the upper left-hand choice in the table).
Thus, firm A will reason that it makes sense to expand output if B holds down output and that it also makes sense to expand output if B raises output. Again, B faces a parallel set of decisions.
The result of this prisoner’s dilemma is often that even though A and B could make the highest combined profits by cooperating in producing a lower level of output and acting like a monopolist, the two firms may well end up in a situation where they each increase output and earn only \(\$400\) each in profits. The following Clear It Up feature discusses one cartel scandal in particular.
What is the Lysine cartel?
Lysine, a \(\$600\) million-a-year industry, is an amino acid used by farmers as a feed additive to ensure the proper growth of swine and poultry. The primary U.S. producer of lysine is Archer Daniels Midland (ADM), but several other large European and Japanese firms are also in this market. For a time in the first half of the 1990s, the world’s major lysine producers met together in hotel conference rooms and decided exactly how much each firm would sell and what it would charge. The U.S. Federal Bureau of Investigation (FBI), however, had learned of the cartel and placed wire taps on a number of their phone calls and meetings.
From FBI surveillance tapes, following is a comment that Terry Wilson, president of the corn processing division at ADM, made to the other lysine producers at a 1994 meeting in Mona, Hawaii:
I wanna go back and I wanna say something very simple. If we’re going to trust each other, okay, and if I’m assured that I’m gonna get \(67,000\) tons by the year’s end, we’re gonna sell it at the prices we agreed to . . . The only thing we need to talk about there because we are gonna get manipulated by these [expletive] buyers—they can be smarter than us if we let them be smarter. . . . They [the customers] are not your friend. They are not my friend. And we gotta have ‘em, but they are not my friends. You are my friend. I wanna be closer to you than I am to any customer. Cause you can make us ... money. ... And all I wanna tell you again is let’s—let’s put the prices on the board. Let’s all agree that’s what we’re gonna do and then walk out of here and do it.
The price of lysine doubled while the cartel was in effect. Confronted by the FBI tapes, Archer Daniels Midland pled guilty in 1996 and paid a fine of \(\$100\) million. A number of top executives, both at ADM and other firms, later paid fines of up to \(\$350,000\) and were sentenced to 24–30 months in prison.
In another one of the FBI recordings, the president of Archer Daniels Midland told an executive from another competing firm that ADM had a slogan that, in his words, had “penetrated the whole company.” The company president stated the slogan this way: “Our competitors are our friends. Our customers are the enemy.” That slogan could stand as the motto of cartels everywhere.
Other Game Theory Concepts
A Repeated Game
These are games that are played over and over again. When this happens, players learn more about the game and the players with each play of the game. Think about when you were young and played tic-tac-toe for the first time. The person who you played with was an experienced player and they beat you. However, you learned quickly about the strategies that you needed to use to keep them from earning three "Xs" or "Os" in a row. This is an example of a repeated game. Now every game ends in "Cats-Eye" or a draw.
Repeated games may induce players to cooperate. If you get to know other players well and know their strategies, this could build trust or at least predictability in their moves.
Maximin Strategy
A strategy that allows players to avoid the largest losses is the Maximin Strategy (or the safety first strategy). In other words, this is a strategy that maximizes the minimum payoff for one player. This strategy can be identified by identifying the worst possible outcome for each strategy. Players choose the best "worst case" strategy (where the lowest payoff is the highest).

Caption: Firm 1 and Firm 2 can either choose to Not Invest or Invest. If Firm 1 chooses to Invest and Firm 2 chooses to Invest, Firm 1's payoff will be $20. If Firm 1 chooses to Invest and Firm 2 chooses to Don't Invest, Firm 1's payoff will be -$100. If Firm 1 chooses to Don't Invest and Firm 2 chooses to Invest, Firm 1's payoff will be $15. If Firm 1 chooses to Don't Invest and Firm 2 chooses to Don't Invest, Firm 1's payoff will be $10. In this case, the best worst case scenario for Firm 1 will be to DON'T INVEST. (Check your Understanding: Firm 2s maximin strategy will be to INVEST.)
How to Enforce Cooperation
How can parties who find themselves in a prisoner’s dilemma situation avoid the undesired outcome and cooperate with each other? The way out of a prisoner’s dilemma is to find a way to penalize those who do not cooperate.
Perhaps the easiest approach for colluding oligopolists, as you might imagine, would be to sign a contract with each other that they will hold output low and keep prices high. If a group of U.S. companies signed such a contract, however, it would be illegal. Certain international organizations, like the nations that are members of the Organization of Petroleum Exporting Countries (OPEC), have signed international agreements to act like a monopoly, hold down output, and keep prices high so that all of the countries can make high profits from oil exports. Such agreements, however, because they fall in a gray area of international law, are not legally enforceable. If Nigeria, for example, decides to start cutting prices and selling more oil, Saudi Arabia cannot sue Nigeria in court and force it to stop.
Because oligopolists cannot sign a legally enforceable contract to act like a monopoly, the firms may instead keep close tabs on what other firms are producing and charging. Alternatively, oligopolists may choose to act in a way that generates pressure on each firm to stick to its agreed quantity of output.
One example of the pressure these firms can exert on one another is the kinked demand curve, in which competing oligopoly firms commit to match price cuts, but not price increases. This situation is shown in Figure \(\PageIndex{1}\). Say that an oligopoly airline has agreed with the rest of a cartel to provide a quantity of \(10,000\) seats on the New York to Los Angeles route, at a price of \(\$500\). This choice defines the kink in the firm’s perceived demand curve. The reason that the firm faces a kink in its demand curve is because of how the other oligopolists react to changes in the firm’s price. If the oligopoly decides to produce more and cut its price, the other members of the cartel will immediately match any price cuts—and therefore, a lower price brings very little increase in quantity sold.
If one firm cuts its price to \(\$300\), it will be able to sell only \(11,000\) seats. However, if the airline seeks to raise prices, the other oligopolists will not raise their prices, and so the firm that raised prices will lose a considerable share of sales. For example, if the firm raises its price to \(\$550\), its sales drop to \(5,000\) seats sold. Thus, if oligopolists always match price cuts by other firms in the cartel, but do not match price increases, then none of the oligopolists will have a strong incentive to change prices, since the potential gains are minimal. This strategy can work like a silent form of cooperation, in which the cartel successfully manages to hold down output, increase price, and share a monopoly level of profits even without any legally enforceable agreement.
A Kinked Demand Curve
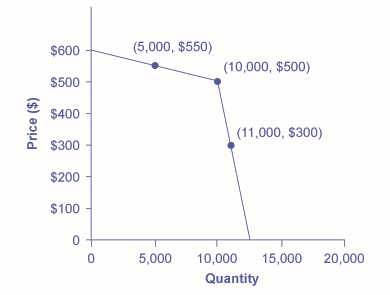
Figure \(\PageIndex{1}\): Consider a member firm in an oligopoly cartel that is supposed to produce a quantity of 10,000 and sell at a price of $500. The other members of the cartel can encourage this firm to honor its commitments by acting so that the firm faces a kinked demand curve. If the oligopolist attempts to expand output and reduce price slightly, other firms also cut prices immediately—so if the firm expands output to 11,000, the price per unit falls dramatically, to $300. On the other side, if the oligopoly attempts to raise its price, other firms will not do so, so if the firm raises its price to $550, its sales decline sharply to 5,000. Thus, the members of a cartel can discipline each other to stick to the pre-agreed levels of quantity and price through a strategy of matching all price cuts but not matching any price increases.
Many real-world oligopolies, prodded by economic changes, legal and political pressures, and the egos of their top executives, go through episodes of cooperation and competition. If oligopolies could sustain cooperation with each other on output and pricing, they could earn profits as if they were a single monopoly. However, each firm in an oligopoly has an incentive to produce more and grab a bigger share of the overall market; when firms start behaving in this way, the market outcome in terms of prices and quantity can be similar to that of a highly competitive market.
Tradeoffs of Imperfect Competition
Monopolistic competition is probably the single most common market structure in the U.S. economy. It provides powerful incentives for innovation, as firms seek to earn profits in the short run, while entry assures that firms do not earn economic profits in the long run. However, monopolistically competitive firms do not produce at the lowest point on their average cost curves. In addition, the endless search to impress consumers through product differentiation may lead to excessive social expenses on advertising and marketing.
Oligopoly is probably the second most common market structure. When oligopolies result from patented innovations or from taking advantage of economies of scale to produce at low average cost, they may provide considerable benefit to consumers. Oligopolies are often buffeted by significant barriers to entry, which enable the oligopolists to earn sustained profits over long periods of time. Oligopolists also do not typically produce at the minimum of their average cost curves. When they lack vibrant competition, they may lack incentives to provide innovative products and high-quality service.
The task of public policy with regard to competition is to sort through these multiple realities, attempting to encourage behavior that is beneficial to the broader society and to discourage behavior that only adds to the profits of a few large companies, with no corresponding benefit to consumers. Monopoly and Antitrust Policy discusses the delicate judgments that go into this task.
Example \(\PageIndex{1}\): The Temptation to Defy the Law
Oligopolistic firms have been called “cats in a bag,” as this chapter mentioned. The French detergent makers chose to “cozy up” with each other. The result? An uneasy and tenuous relationship. When the Wall Street Journal reported on the matter, it wrote: “According to a statement a Henkel manager made to the [French anti-trust] commission, the detergent makers wanted ‘to limit the intensity of the competition between them and clean up the market.’ Nevertheless, by the early 1990s, a price war had broken out among them.” During the soap executives’ meetings, which sometimes lasted more than four hours, complex pricing structures were established. “One [soap] executive recalled ‘chaotic’ meetings as each side tried to work out how the other had bent the rules.” Like many cartels, the soap cartel disintegrated due to the very strong temptation for each member to maximize its own individual profits.
How did this soap opera end? After an investigation, French antitrust authorities fined Colgate-Palmolive, Henkel, and Proctor & Gamble a total of €\(361\) million(\(\$484\) million). A similar fate befell the icemakers. Bagged ice is a commodity, a perfect substitute, generally sold in \(7\)- or \(22\)-pound bags. No one cares what label is on the bag. By agreeing to carve up the ice market, control broad geographic swaths of territory, and set prices, the icemakers moved from perfect competition to a monopoly model. After the agreements, each firm was the sole supplier of bagged ice to a region; there were profits in both the long run and the short run. According to the courts: “These companies illegally conspired to manipulate the marketplace.” Fines totaled about \(\$600,000\)—a steep fine considering a bag of ice sells for under \(\$3\) in most parts of the United States.
Even though it is illegal in many parts of the world for firms to set prices and carve up a market, the temptation to earn higher profits makes it extremely tempting to defy the law.
Key Concepts and Summary
An oligopoly is a situation where a few firms sell most or all of the goods in a market. Oligopolists earn their highest profits if they can band together as a cartel and act like a monopolist by reducing output and raising price. Since each member of the oligopoly can benefit individually from expanding output, such collusion often breaks down—especially since explicit collusion is illegal.
The prisoner’s dilemma is an example of game theory. It shows how, in certain situations, all sides can benefit from cooperative behavior rather than self-interested behavior. However, the challenge for the parties is to find ways to encourage cooperative behavior.
References
The United States Department of Justice. “Antitrust Division.” Accessed October 17, 2013. http://www.justice.gov/atr/.
eMarketer.com. 2014. “Total US Ad Spending to See Largest Increase Since 2004: Mobile advertising leads growth; will surpass radio, magazines and newspapers this year. Accessed March 12, 2015. http://www.emarketer.com/Article/Tot...e-2004/1010982.
Federal Trade Commission. “About the Federal Trade Commission.” Accessed October 17, 2013. http://www.ftc.gov/ftc/about.shtm.
Glossary
- cartel
- a group of firms that collude to produce the monopoly output and sell at the monopoly price
- collusion
- when firms act together to reduce output and keep prices high
- duopoly
- an oligopoly with only two firms
- game theory
- a branch of mathematics often used by economists that analyzes situations in which players must make decisions and then receive payoffs based on what decisions the other players make
- kinked demand curve
- a perceived demand curve that arises when competing oligopoly firms commit to match price cuts, but not price increases
- prisoner’s dilemma
- a game in which the gains from cooperation are larger than the rewards from pursuing self-interest


