10.5: The Long-Run Neutrality of Money
- Page ID
- 11848
There is a long historic tradition of discussing money, economic activity, and prices based on the equation of exchange. In terms of real GDP, that equation is an identity, true by definition, namely:
\[MV \equiv PY\]
Equation of exchange: the identity between total money expenditure and nominal GDP.
Suppose M is the money supply, V the velocity of circulation or the number of times a unit of money changes hands in a given time period, and P the flexible general price level like the GDP deflator, and Y real GDP. Then, in the equation of exchange, the total of expenditure, MV, is by definition equal to the money value of goods and services bought.
The equation of exchange is the foundation of the famous quantity theory of money, a theory of the price level or the inflation rate. Assume that V, the velocity of circulation of money is a constant, V0. This velocity of circulation is just the inverse of the demand for money, L, based on the current financial structure and practice of making payments, without the effect of interest rates on that demand for money balances.
Assume as well that the economy operates at the level of potential real GDP, YP. Further assume that the money supply is determined and firmly controlled by the central bank. Based on these assumptions, the quantity theory of money says that the price level P is determined by the size of the money supply. This can be written as follows:
\(MV_0 = PY_p\)
or restated as:
\[P = M \times \frac{V_0}{Y_p}\]
With (V0/YP) a constant, a change in money supply M causes a change in P. If M doubles then P doubles. If M grows at 10 percent a year then P grows at 10 percent a year. The inflation rate is determined by the rate of growth of the money supply.
Neutrality of money: monetary policy can set prices and inflation rates in the long run, but not output and employment.
By this quantity theory of money and the price level, money is neutral. Changes in the money supply have no effect on the level of real output. Real output is constant at YP. Central bank or government control of the money supply gives the policy authorities control of the price level and the inflation rate.
Current approaches to monetary policy recognize that the conditions assumed by the quantity theory are not met in the short run. The demand for money is variable and thus the velocity of circulation is not constant. Real GDP and real GDP growth rates fluctuate about the trend of potential output. Prices in some markets are sticky and slow to adjust to changes in demand. The central bank’s control of the money supply and the growth rate of the money supply are not precise. The quantity theory and the neutrality of money have important long-run implications but short-run conditions call for a different approach.
Monetary policy as described by the policy rule targets inflation by stabilizing output at potential output. In short time periods, prices tend to be sticky. This means that the central bank is able to change nominal interest rates more rapidly than prices change. Changes in the interest rates then change aggregate demand through the transmission mechanism we examined in Chapter 9.
Longer-term inflation targets are met by keeping actual output close to potential output. In an aggregate supply and demand model, prices or inflation rates change as a result of persistent recessionary or inflationary gaps. If monetary policy can reduce or eliminate the gaps by shifting the AD curve, it stabilizes both output and inflation.
What monetary policy cannot do is change potential output. Suppose in Figure 10.7 the central bank decides it could raise output above YP and lower the unemployment rate below the natural rate un. The central bank then sets the interest rate lower at i1. According to the transmission mechanism, AD increases and Y increases. The short-run effect of this shift to monetary expansion is, indeed, to increase output and employment and lower the unemployment rate creating an inflationary gap (Y1 − YP).
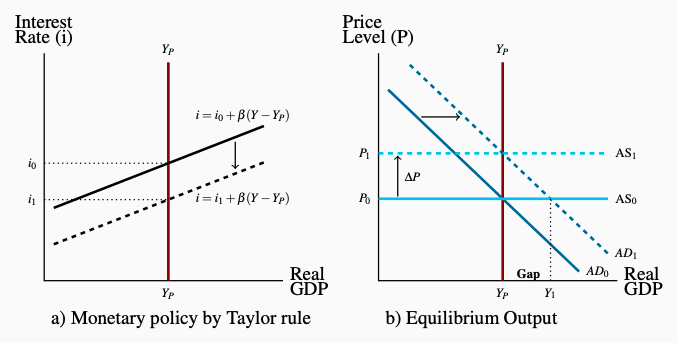
Figure 10.7: The Neutrality of Money
Starting with monetary policy \(I = i_0 + \beta(Y − YP)\) equilibrium at P0Y0, an
expansionary monetary policy lowers i from i0 to i1 with a corresponding
increase in money supply. Lower i shifts AD from AD0 to AD1, causes
a short run increase in Y to Y1 and creates an inflationary gap. If this gap
persists it pushes wages and prices up shifting AS to AS1 at the price level
P1. Expansionary monetary policy introduced at Y = YP. It does not make a
lasting change in real GDP but it just increases P. Money is neutral.
But if the inflationary gap created by expansionary monetary policy persists, costs and prices will rise. Low unemployment rates, high rates of utilization of plant and equipment, and strong demand for other inputs to production raise input prices and production costs, as we will discuss in more detail in Chapters 11 and 12. With strong demand for final output, higher costs result in higher prices. Rising prices reduce expenditure until output falls back to potential output. The only lasting effect of expansionary monetary policy is the higher price level P1.
In the long run, money is neutral. Monetary policy can change the price level or the inflation rate in the long run, but it cannot change potential output. As a result, central banks set inflation targets for monetary policy, not output or employment targets.


