6.5: The Multiplier: Changes in Aggregate Expenditure and Equilibrium Output
- Page ID
- 11820
In our model the slope of the AE line depends on the marginal propensity to consume and the marginal propensity to import. For any given MPC and MPM, the level of autonomous expenditure \(C_0 + I_0 + X_0 − IM_0\) determines the height of the AE line. Recall that autonomous expenditure is expenditure that is not related to national income.
Changes in autonomous expenditure cause parallel vertical shifts in the AE function. Investment expenditure depends chiefly on firms’ current expectations about future demand for their output and future profits. These expectations about the size and strength of future markets can fluctuate significantly, influenced by current pessimism or optimism about the future. We saw this volatility in investment in Figure 6.6. Similarly, changes in conditions in export markets change exports and changes in consumer confidence change autonomous consumption expenditure.
Suppose firms become very optimistic about future demand for their output. They want to expand their factories and add new equipment to meet this future demand. Planned investment rises. If other components of aggregate expenditure are unaffected, AE will be higher at each income than before. Figure 6.10 shows this upward shift in AE to AE1. Before we go into detail, think about what is likely to happen to output. It will rise, but by how much?
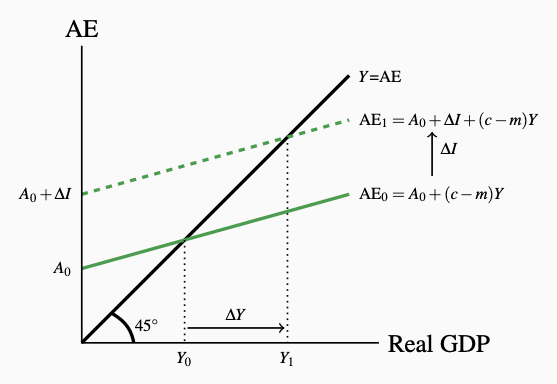
FIgure 6.10: The Effect of a Rise in Investment
A rise in investment ∆I shifts AE up to AE1. Equilibrium GDP rises by a
larger amount from Y0 to Y1.
When investment rises, firms increase output, increasing their payments for factor inputs to production. Households have higher income and increase their consumption expenditure (c∆Y) and imports (m∆Y). Firms increase output again to meet this increased demand, further increasing household incomes. Consumption and imports rise further. What brings this process of rising output and income to an end?
Figure 6.10 shows that an upward shift in the AE function increases equilibrium income by a finite amount, but by a larger amount than the vertical rise in the AE line. This is because \(c − m\), the slope of AE, is less than unity, giving the AE line a lower slope than the 45° line. Households increase their expenditure when incomes rise, but they increase expenditure by less than the rise in income. Equilibrium moves from Y0 to Y1. Equilibrium output rises more than the original rise in investment, ∆Ye > ∆I, but does not rise without limit.
We can also show the change in equilibrium output caused by a rise in autonomous investment expenditure using the simple algebra we used earlier. As before, start with:
\(Consumption: \hfill C = 20 + 0.8Y\)
{\text{Investment:}} \hfill {I = 20}%
{\text{Exports:}} \hfill {X = 50}%
{\text{Imports:}} \hfill {IM = 10 + 0.2Y}%
{\text{Aggregate expenditure:}} \hfill {AE = 80 + 0.6Y} \hfill%\)
Then, equilibrium requires output (Y) equal to aggregate expenditure (AE):
\(\begin{align*} Y &= 80 + 0.6Y \\
(1 - 0.6)Y &= 80 \\
Y &= \displaystyle\frac {80}{(1 - 0.6)} \\
Y &= 200 \end{align*}\)
Now suppose investment increases by 10 to \(I = 30\) and AE increases to \(AE = 90 + 0.6Y\).
Equilibrium still requires output (Y) equal to aggregate expenditure (AE), but now:
\(\begin{align*} Y &= 90 + 0.6Y \\
(1 - 0.6)Y &= 90 \\
Y &= \displaystyle\frac {90}{(1 - 0.6)} \\
Y &= 225 \end{align*}\)
A rise in autonomous investment expenditure by 10 has increased equilibrium output and income by 25, from 200 to 225. This is an algebraic example of the effect of the increase in investment illustrated by Figure 6.10. The algebra gives us the equilibrium output under two different levels of autonomous investment expenditure. But it does not show us the adjustment process. The key to that process is the induced expenditure coming from the marginal propensities to consume and import.
A rise of 10 in investment expenditure causes a rise of 25 in equilibrium output. Higher investment expenditure induces a rise in output and income that induces a further rise in consumption expenditure and imports. Total expenditure rises by more than the original rise in investment, but the process does not spiral out of control because the marginal propensities to spend are less than 1. Expenditure increases in diminishing steps until equilibrium output is 225.
The multiplier is a concept used to define the change in equilibrium output and income caused by a change in autonomous expenditure. If A is autonomous expenditure:
\[\text{The multiplier} = \displaystyle\frac {\Delta Y}{\Delta A}\]
Multiplier (∆Y/∆A): the ratio of the change in equilibrium income Y to the change in autonomous expenditure A that caused it.
In our example, the initial change in autonomous expenditure \(\Delta I = \Delta A\) is 10, and the final change in equilibrium output ∆Y is 25. The multiplier is \(\Delta I/\Delta A = 25/10 = 2.5\). That is why in Figure 6.10, a small upward shift in the AE line leads to a much larger increase in equilibrium output and income.
The Size of the Multiplier
The multiplier is a number that tells us how much equilibrium output changes as a result of a change in autonomous expenditure. The multiplier is bigger than 1 because a change in autonomous expenditure changes income and sets off further changes in induced expenditure. The marginal propensities to consume and import determine the induced expenditure.
The size of the multiplier depends on the sizes of the marginal propensities to consume and import. The initial effect of a unit rise in autonomous investment expenditure is to raise output and income by one unit. If the (MPC − MPM) is large, this rise in income causes a large rise in induced expenditure, and the multiplier is large. If the (MPC − MPM) is small, a given change in autonomous expenditure and output induces only small changes in expenditure, and the multiplier is small.
To find the multiplier, add all the increases in aggregate expenditure and output from each step in Table 6.3 below, based on c = 0.8 and m = 0.2 as follows:
\(\text{Multiplier} = 1 + (0.8 - 0.2) + (0.8 - 0.2)^2 + (0.8 - 0.2)^3 + ...\)
The dots at the end mean we keep adding terms such as (0.8−0.2)4 and so on. The right-hand side of the equation is a geometric series. Each term is (0.8−0.2) times the previous term. Fortunately, mathematicians have shown that there is a general formula for the sum of all terms in such a series, which gives:
\(\text{Multiplier} = \displaystyle\frac{1}{(1 - (0.8 - 0.2))} = \displaystyle\frac{1}{(1 - 0.6)}\)
The formula applies whatever the (constant) values of c and m, the marginal propensities to consume and import, as follows:
\[\text{Multiplier} = \frac{1}{(1-c+m)}\]
For the particular values of c = 0.8 and m = 0.2, Equation 6.9 confirms that the multiplier is 1/(1−0.6), which is 1/0.4 = 2.5. Hence, a rise in investment expenditure by 10 causes a rise in equilibrium output by 25, as we know from Table 6.3. Similarly, the multiplier allows us to predict that a fall in investment expenditure by 10 would lower equilibrium output and income by 25, if c = 0.8 and m = 0.2. Indeed, you will probably have guessed this from Equation 6.9. Equilibrium output is simply autonomous expenditure multiplied by the multiplier!
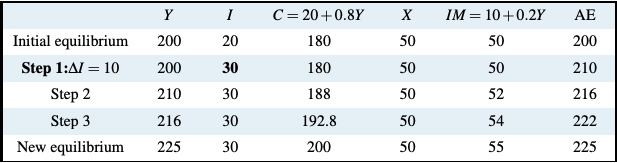
Table 6.3: The Multiplier Effects of an Increase in Investment (∆I = 10) on Equilibrium GDP
In more general terms, because MPC − MPM = c − m is the slope of the AE function, we can write:
\[\text{Multiplier} = \displaystyle\frac{1}{(1 - \text{slope of AE})}\]
In the model we have here, the slope of AE is MPC − MPM, but this formula for the multiplier will still be useful when we introduce the tax system in the government sector in Chapter 7.
Leakages, Injections & Equilibrium Output
Equilibrium output equals planned expenditure on consumption, investment, and exports net of imports. This also means that planned investment and exports equal planned saving and imports. If Y = C + I + X − IM, then Y − C + IM = I + X. From Equation 6.3, Y − C = S, and thus,
\[S + IM = I + X\]
This condition holds only when aggregate expenditure is at the right level to achieve equilibrium.
Savings and imports are leakages from the expenditure stream that do not pass current income on to business through expenditure on current output. On the other hand, autonomous investment and exports are injections into expenditure and a flow of funds to business that is independent of current income. When these injections just offset the leakages, aggregate expenditure equals output and the economy is in equilibrium.
In modern economies, business managers make investment decisions and residents of other countries make decisions about expenditure on domestic exports. Household expenditure plans depend on their income. Since planned saving and imports depend on income but planned investment and exports do not, Equation 6.11 means that output and income adjust to establish equilibrium by making savings and import plans by households (leakages) equal to the investment plans of firms and export plans of non- residents (injections). Figure 6.11 illustrates this equilibrium condition.
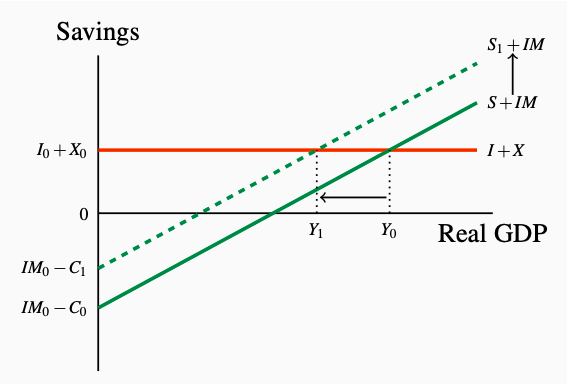
Figure 6.11: Equilibrium when Planned Leakages Equal Planned Injections
At equilibrium Y0 planned saving plus imports equal planned investment
plus exports. An increase in saving to S1 lowers equilibrium Y to Y1.
This equilibrium condition also reveals the paradox of thrift whereby an attempt to increase aggregate saving in the economy results in a lower equilibrium GDP but unchanged aggregate saving. In Figure 6.11 the increase in the rate of saving (S/Y) shifts the S + M up to S1 + IM. This increase in leakages lowers aggregate expenditure at Y0 and output falls to Y1. The paradox is that the attempt to increase savings causes a decrease in national income and leaves leakages S + IM unchanged. S1 + IM at Y1 equals S + IM at Y0.
Paradox of thrift: attempts to increase aggregate national saving cause changes in equilibrium GDP that leave saving unchanged.
Interest in this paradox has returned following the financial crisis and recession of 2008-09 as households in many countries tried to reduce their debt loads by raising the saving rate. Aggregate expenditure was further reduced by reduced consumption expenditures, adding to the recession As we will see in Chapter 7 the paradox can also frustrate government attempts to eliminate budget deficits by austerity programs when economies are in recession.


