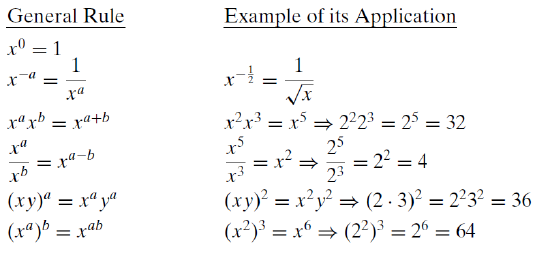3.1: Initial Solution
- Last updated
- Save as PDF
- Page ID
- 58444
What you know so far:
- The budget constraint shows the consumer’s possible consumption bundles. The standard, linear constraint is \(p_1x_1 + p_2x_2 = m\). There are many other situations, such as subsidies and rationing, which give more complicated constraints with kinks and horizontal/vertical segments.
- The indifference map shows the consumer’s preferences. The standard situation is a set of convex, downward sloping indifference curves. There are many alternative preferences, such as perfect substitutes and perfect complements. Preferences are captured by utility functions, which accurately reflect the shape of the indifference curves.
Our job is to combine these two parts, one expressing what is affordable and the other what is desirable, to find the combination (or bundle) that maximizes satisfaction (as described by the indifference map or utility function) given the budget constraint. The answer will be in terms of how much the consumer will buy in units of each good.
The optimal solution is depicted by the canonical graph in Figure 3.1. The word canonical is used here to mean standard, conventional, or orthodox. In economics, a canonical graph is a core, essential graph that is understood by all economists, such as a supply and demand graph.
It is no exaggeration to say that Figure 3.1 is one of the most fundamental and important graphs in economics. It is the foundation of the Theory of Consumer Behavior and with it we will derive a demand curve.
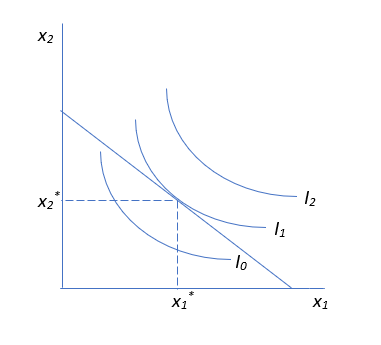 Figure 3.1: The canonical graph of the optimal solution.
Figure 3.1: The canonical graph of the optimal solution.One serious intellectual obstacle with Figure 3.1 is that it is highly abstract. Below we work on a concrete problem, with actual numbers, to explain what is going on in this fundamental graph.
Before we dive in, we need to discuss solution strategies. There are two ways to find the optimal solution:
1. Analytical methods using algebra and calculusthis is the conventional, paper and pencil approach that has been used for a long time.
2. Numerical methods using a computer, for example, Excel’s Solverthis is a modern solution strategy that uses the computer to do most of the work.
Analytical Approach
Unfortunately, constrained optimization problems are harder to solve than unconstrained problems. The appendix to this chapter offers a short calculus review along with a few common derivative and algebra rules. If the material below makes little sense, go to the appendix and then return here.
Because this is a constrained optimization problem, the analytical approach uses the method developed by Joseph Louis Lagrange. His brilliant idea is based on transforming a constrained optimization problem into an unconstrained problem and then solving by using standard calculus techniques. In the process, a new endogenous variable is created. It can have a meaningful economic interpretation.
Lagrange gave us a recipe to follow that requires four steps:
1. Rewrite the constraint so that it is equal to zero.
2. Form the Lagrangean function.
3. Take partial derivatives with respect to \(x_1\), \(x_2\), and \(\lambda\).
4. Set the derivatives equal to zero and solve for \(x_1\mbox{*}\), \(x_2\mbox{*}\), and \(\lambda\mbox{*}\).
A Concrete Example
Suppose a consumer has a Cobb-Douglas utility function with exponents both equal to 1 and a budget constraint, \(2x_1 + 3x_2 = 100\) (which means the price of good 1 is $2/unit, the price of good 2 is $3/unit, and income is $100).
The problem is to maximize utility subject to (s.t.) the budget constraint. It is written in equation form like this: \[\max\limits_{x_1,x_2}U(x_1,x_2)=x_1x_2 \\ \textrm{s.t. } 100 = 2x_1 + 3x_2 \nonumber \]
This problem is not solved directly. It is first transformed into an unconstrained problem, and then this unconstrained problem is solved. Here is how we apply the recipe developed by Lagrange.
1. Rewrite the constraint so that it is equal to zero.
\(0 = 100 - 2x_1 - 3x_2\)
2. Form the Lagrangean function.
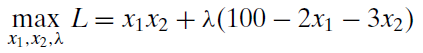
Most math books use a fancy script L for the Lagrangean, like this \(\mathcal{L}\), but this is difficult to do in Word’s Equation Editor (which you will be using) so an extra-large L will work just as well. Also, many books spell Lagrangean with an i, Lagrangian, but both spellings are acceptable.
Note that the Lagrangean function, L, is composed of the original objective function (in this case, the utility function) plus a new variable, the Greek letter lambda, \(\lambda\), times the rewritten constraint. Called the Lagrangean multiplier, \(\lambda\) is a new endogenous variable that is introduced as part of Lagrange’s solution strategy.
The next step in Lagrange’s recipe can be intimidating. This is not the time to rush through and turn the page. Refer to the appendix at the end of this section if things start to get confusing.
3. Take partial derivatives with respect to \(x_1\), \(x_2\), and \(\lambda\).
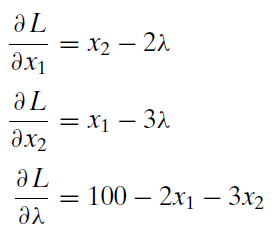
The derivative used here is a partial derivative, denoted by \(\partial\), which is an alternative way of writing a lowercase Greek letter d (which is why the more common symbol for the letter \(\delta\) is also used). The partial derivative symbol is usually read as the letter d, so the first equation read out loud would be “d L d x one equals x two minus two times lambda.” It is also common to read the derivative in the first equation as “partial L partial x one.”
The partial derivative is a natural extension of the regular derivative. Consider the function \(y = 4x^2\). The derivative of y with respect to x is \(\frac{dy}{dx} = 8x\). Suppose, however, that we had a more complicated function, like this: \(y = 4zx^2\). This multivariate function says that y depends on two variables, z and x. We can explore the rate of change of this function along the x axis by treating it as a partial function, meaning that we hold the z variable constant. Then the partial derivative of y with respect to x is \(\partial y/ \partial x = 8zx\). If we hold x constant and vary z, then the partial derivative of y with respect to z is \(\partial y/ \partial z = 4x^2\).
Applying this logic to the Lagrangean in step 2, when we take the partial derivative with respect to \(x_1\), the first term is \(x_2\) because it is as if we had "x4" and took the derivative with respect to x, getting 4.
If we multiply \(\lambda\) through the parenthetical expression in the Lagrangean, we get: \[\lambda (100 - 2x_1 - 3x_2)\\ \lambda 100 - \lambda 2x_1 - \lambda 3x_2 = 0\] The first and third terms on the left-hand side do not have \(x_1\) so the derivative with respect to \(x_1\) is zero (just like the derivative of a constant is zero). The derivative with respect to \(x_1\) of the middle term produces \(- \lambda 2\) which is written by convention as \(- 2 \lambda\).
Can you do the other two derivatives in step 3?
4. Set the derivatives equal to zero and solve for \(x_1\mbox{*}\), \(x_2\mbox{*}\), and \(\lambda\mbox{*}\).
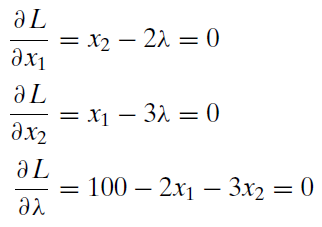
There are many ways to solve this system of equations, which are known as the first-order conditions. Sometimes, this is the hardest part of the Lagrangean method. Depending on the utility function and constraint, there may not be an analytical solution.
A common strategy involves moving the \(\lambda\) terms in the first two equations to the right-hand side and then dividing the first equation by the second one.
\[ x_2 = 2 \lambda \\ x_1 = 3 \lambda \\ \frac{x_2}{x_1}=\frac{2 \lambda}{3 \lambda}\] The \(\lambda\) terms then cancel out, leaving us with two equations (the one above and the third equation from the original three first-order conditions) and two unknowns (\(x_1\) and \(x_2\)). \[\begin{gathered} %star suppresses line # \frac{x_2}{x_1} = \frac{2}{3}\\ 100 - 2x_1 - 3x_2 = 0\end{gathered}\] The top equation has a nice economic interpretation. It says that, at the optimal solution, the MRS (slope of the indifference curve) must equal the price ratio (slope of the budget constraint).
From the top equation, we can solve for \(x_2\). \[x_2=\frac{2}{3}x_1\]
We can then substitute this expression into the bottom equation (the budget constraint) to get the optimal value of \(x_1\).
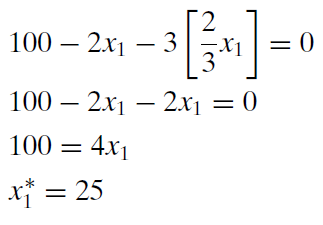
Then we substitute \(x_1\mbox{*}\) into the expression for \(x_2\) to get \(x_2\mbox{*}\). \[x_2=\frac{2}{3}[25]\] \[x_2\mbox{*}=16\frac{2}{3}\] The asterisk is used to represent the optimal solution for a choice variable. This work says that this consumer should buy 25 units of good 1 and \(16 \frac{2}{3}\) units of good 2 in order to maximize satisfaction given the budget constraint. We can use either equation 1 or 2 from the original first-order conditions to find the optimal value of \(\lambda\). Either way, we get \(\lambda\mbox{*} = 8 \frac{1}{3}\).
For many optimization problems, we would be interested in knowing the numerical value of the maximum by evaluating the objective function (in this case the utility function) at the optimal solution. But recall that utility is measured only up to an ordinal scale and the actual value of utility is irrelevant. We want to maximize utility, but we do not care about its actual maximum value. The fact that utility is ordinal, not cardinal, also explains why the optimal value of lambda is not meaningful. In general, the Lagrangean multiplier tells us how the maximum value of the objective function changes as the constraint is relaxed. With utility as the objective function, this interpretation is not applicable.
Numerical Approach
Instead of calculus (via the method of Lagrange) and pencil and paper, we can use numerical methods to find the optimal solution.
To use the numerical approach, we need to do some preliminary work. We have to set up the problem in Excel, carefully organizing things into a goal, endogenous variables, exogenous variables, and constraint. Once we have everything organized, we can use Excel’s Solver to get the solution.
STEP Open the Excel workbook OptimalChoice.xls, read the Intro sheet, and then go to the OptimalChoice sheet to see how the numerical approach can be used to solve the problem we worked on above.
Figure 3.2 reproduces the display you see when you first arrive at the OptimalChoice sheet.
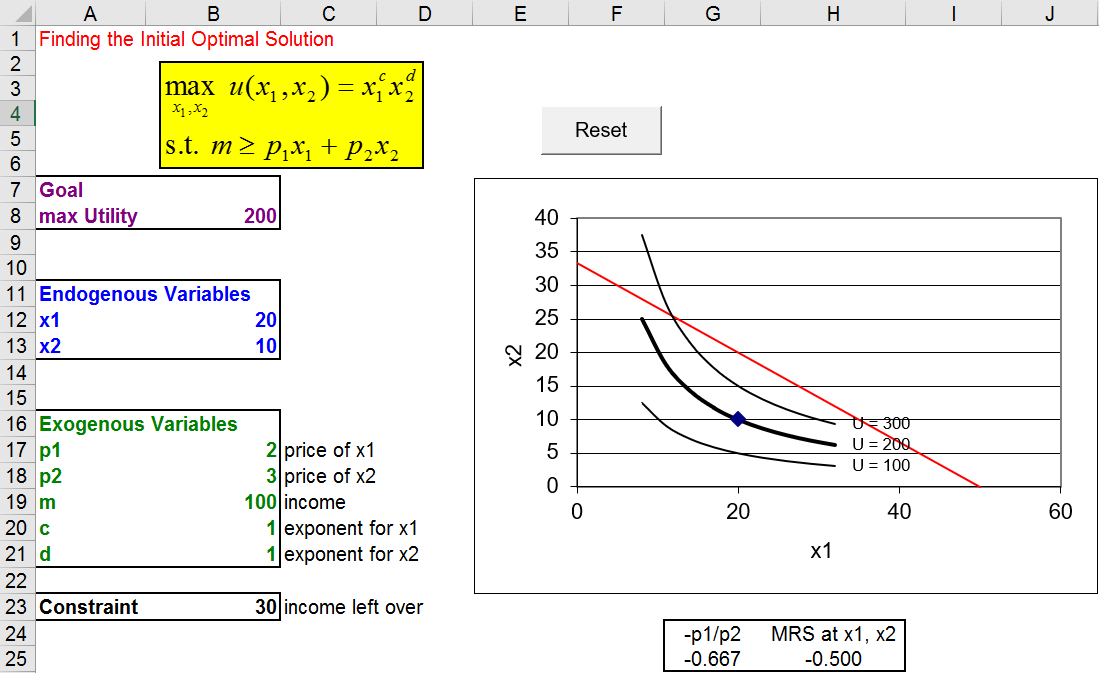
Figure 3.2: The initial display in the OptimalChoice sheet.
Source: OptimalChoice.xls!OptimalChoice
Notice how the sheet is organized according to the three components of the optimization problem: goal, endogenous, and exogenous variables. The constraint cell displays how much of the consumer’s budget remains available for buying goods. The consumer in Figure 3.2 is not using all of the income available so we know satisfaction cannot be maximized at the point 20,10.
STEP Let’s have the consumer buy \(x_2\) with the remaining $30. At $3/unit, 10 additional units of \(x_2\) can be purchased. Enter 20 in the \(x_2\) cell (B13) and hit the Enter key. The chart refreshes to display the point 20,20, which is on the budget constraint, and draws three new indifference curves.
Although 20,20 does exhaust the available income, it is not the optimal solution. While you know the answer is 25,\(16 \frac{2}{3}\), there is another way to tell that the consumer can do better.
STEP Look carefully at the display below the chart. It reveals the MRS does not equal the price ratio. This immediately tells us that something is amiss here.
MRS \(> p_1/ p_2\) tells us that the slope of the indifference curve at that point is greater than the slope of the budget constraint. The consumer cannot change the slope of the budget constraint, but the MRS can be altered by choosing a different the combination of goods. This consumer needs to lower the MRS (in absolute value) to make the two equal. This can be done by moving down the budget constraint.
If the consumer buys 10 more of good 1 (so 30 units of \(x_1\) total), consumption of \(x_2\) must fall by \(6 \frac{2}{3}\) units to \(13 \frac{1}{3}\).
STEP Enter 30 in cell B12 and the formula \(=13 + 1/3\) in B13. Now you are on the other side of the optimal solution. The MRS is less than the price ratio.
You could, of course, continue adjusting the cells manually, but there is a faster way.
STEP Click the Data tab in Excel’s Ribbon (on the top of the screen) and click Solver (grouped under the Analyze tab) or execute Tools: Solver in older versions of Excel to bring up the Solver Parameters dialog box (displayed in Figure 3.3).
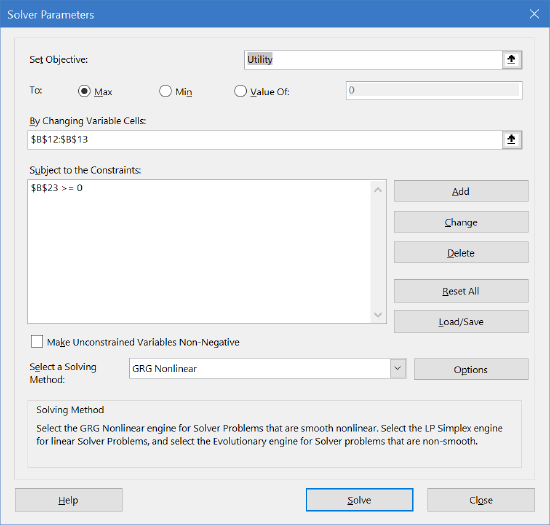 Figure 3.3: Excel’s Solver interface.
Figure 3.3: Excel’s Solver interface.If you do not have Solver available as a choice, bring up the Add-in Manager dialog box and make sure that Solver is listed and checked. If Solver is not listed, you must install it. Solver is included in a standard installation of Excel. For help, try support.office.com or www.solver.com.
Note how Excel’s Solver includes information on the objective function (the target cell), the choice variables (the changing cells), and the budget constraint. These have all been filled in for you, but you will learn how to do this yourself in future work.
STEP Since all of the information has been entered into the Solver Parameters dialog box, simply click the Solve button at the bottom of the dialog box.
Excel’s Solver works by trying different combinations of \(x_1\) and \(x_2\) and evaluating the improvement in the target cell, while trying to stay within the constraint. When it cannot improve very much more, it figures it has found the answer and displays a message as shown in Figure 3.4.
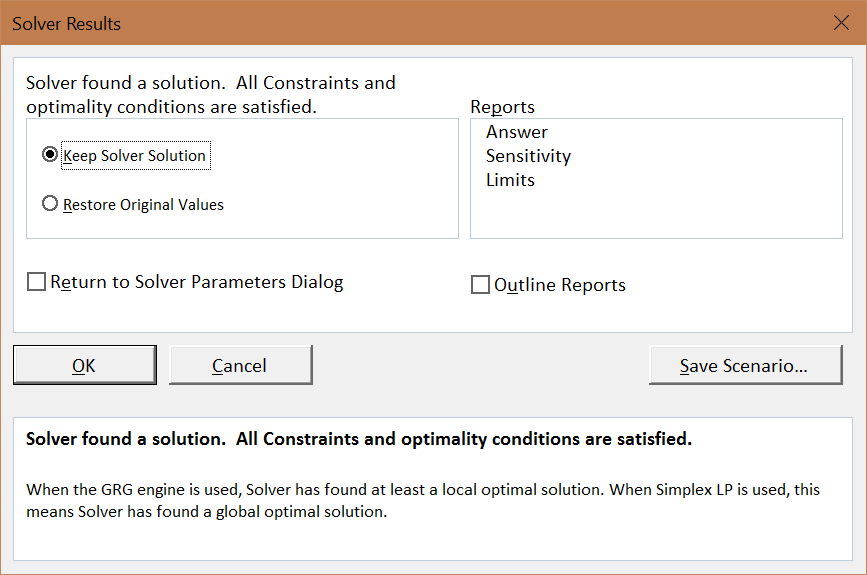 Figure 3.4: Solver reports success.
Figure 3.4: Solver reports success.Although Solver gets the right answer in this problem, we will see in future applications that Solver is not perfect and does not deserve blind trust.
STEP Click the Sensitivity option under Reports and click OK; Excel puts the Solver solution into cells B12 and B13. It also inserts a new sheet into the workbook with the Sensitivity Report.
STEP Click on cells B12 and B13. Notice that Excel did not get exactly 25 and \(16 \frac{2}{3}\). It got extremely close and you can certainly interpret the result as confirming the analytical solution, but Solver’s output requires interpretation and critical thinking by the user. We will focus on the issue of the exactly correct answer later.
STEP Proceed to the Sensitivity Report sheet (inserted by Solver) to confirm that this numerical method gives substantially the same absolute value for the Lagrangean multiplier that we found via the Lagrangean method (\(8 \frac{1}{3}\)). We postpone explanation of this because utility’s ordinal scale makes interpretation of the Lagrangean multiplier pointless. For now, we simply note that Solver can report optimal lambda and its results agreed with the Lagrangean method.
You might notice that Excel reports a Lagrangean multiplier value of -8.33 (with a few more trailing 3s) yet our analytical work did not produce a negative number. It turns out that we ignore the sign of \(\lambda^{*}\). If we set up the Lagrangean as the objective function minus (instead of plus) lambda times the constraint or rewrite the constraint as \(0 = 2x_1 + 3x_2 - 100\) (instead of \(0 = 100 - 2x_1 - 3x_2\)), we would get a negative value for \(\lambda^{*}\) in our analytical work. The way we write the constraint or whether we add or subtract the constraint is arbitrary, so we ignore the sign of \(\lambda^{*}\).
To be clear, unlike the sign, the magnitude of \(\lambda^{*}\) can be meaningful, but it is not in this application because utility is not cardinal. We will, however, see examples where the value of \(\lambda^{*}\) is useful and has an economic interpretation.
Using Analytical and Numerical Methods to Find the Optimal Solution
There are two ways to solve optimization problems:
1. The traditional way uses pencil and paper, derivatives, and algebra. The Lagrangean method is used to solve constrained optimization problems, such as the consumer’s choice problem.
2. Advances in computers have led to the creation of numerical methods to solve optimization problems. Excel’s Solver is an example of a numerical algorithm that can be used to find optimal solutions.
In the chapters that follow, we will continue to use both analytical and numerical approaches. You will see that neither method is perfect and both have strengths and weaknesses.
Exercises
The utility function, \(U = 10x - 0.1x^2 + y\), has a quasilinear functional form. Use this utility function to answer the questions below.
- Suppose the budget line is \(100 = 2x + 3y\). Use the analytical method to find the optimal solution. Show your work.
- Suppose the consumer considers the bundle 0,33.33, buying no x and spending all income on y. Use the MRS compared to the price ratio logic to explain what the consumer will do and why.
- This utility function can be written in a more general form with letters instead of numbers, like this: \(U = ax - bx^c + dy\). If a increases, what happens to the optimal consumption of \(x\mbox{*}\)? Explain how you arrived at your answer.
References
The epigraph is from page 421 of W. W. Rouse Ball’s A Short Account of the History of Mathematics (first published in 1888). Of course, there are many books on the history of mathematics, but this classic is fun and easy to read. It mixes stories about people with real mathematical content.
This entire book (and many others) is freely available at books.google.com. You can read it online or download it as a pdf file.
Appendix: Derivatives and Optimization
A derivative is a mathematical expression that tells you how y in a function \(y = f(x)\) changes given an infinitesimally small change in x. Graphically, it is the slope, or rate of change, of the function at that particular value of x.
Linear functions have a constant slope and, therefore, a constant value for the derivative. For the linear function \(y = 6 + 3x\), the derivative of y with respect to x is written \(\frac{dy}{dx}\) (pronounced “d y d x”) and its value is 3. This tells you that every time the x variable goes up, the y variable goes up threefold. So, if x increases by 1 unit, y will increase by 3 units. This is easy to see in Figure 3.5.
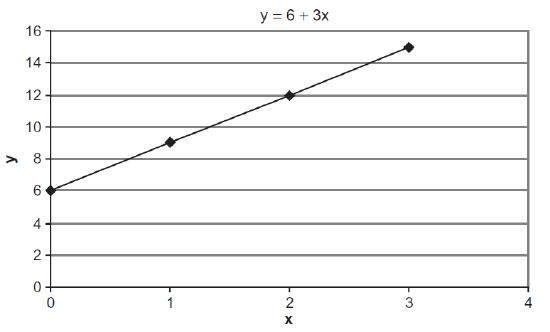 Figure 3.5: A linear function.
Figure 3.5: A linear function.Nonlinear functions have a changing slope and, therefore, a derivative that takes on different values at different values of x. Consider the function \(y = 4x - x^2\). Figure 3.6 graphs this function. Its derivative is \(\frac{dy}{dx} = 4 - 2x\). When evaluated at a specific point, such as \(x = 1\), the derivative is the slope of the tangent line at that point.
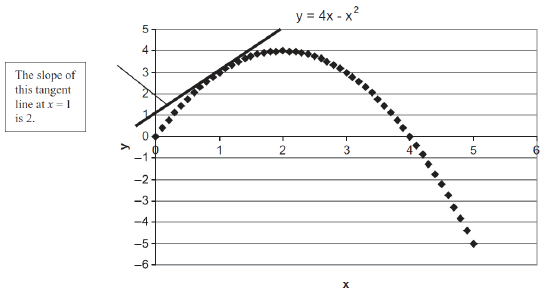 Figure 3.6: A nonlinear function with tangent line at \(x=1\).
Figure 3.6: A nonlinear function with tangent line at \(x=1\).Unlike the previous case, this derivative has x in it. This means this function is nonlinear. The slope depends on the value of x. At \(x=1\), the derivative is 2, but at \(x=2\), it is zero (\(4-2[2]\)) and at \(x=3\), it is -2 (\(4-2[3]\)).
In addition, because it is nonlinear, the size of the change in x affects the measured rate of change. For example, the change in y from \(x = 1\) to \(x = 2\) is 1 (because we move from \(y = 3\) to \(y = 4\) as we increase x by 1). If we increase x by a smaller amount, say 0.1 (from 1 to 1.1), then \(\frac{\Delta y}{\Delta x}=\frac{3.19-3}{1.1-1} = 1.9\). By taking a smaller change in x, we get a different measure of the rate of change.
If we compute the rate of change via the derivative, by evaluating \(4 - 2x\) at x = 1, we get 2. The derivative computes the rate of change for an infinitesimally small change in x. The smaller the change in x, the closer \(\frac{\Delta y}{\Delta x}\) gets to \(\frac{dy}{dx}\). You can see this happening as \(\frac{\Delta y}{\Delta x}\) went from 1 to 1.9 as \(\Delta x\) fell from 1 to 0.1. If we go even smaller, making \(\Delta x\) = 0.01 (going from 1 to 1.01), then \(\frac{\Delta y}{\Delta x}=\frac{3.0199-3}{1.01-1} = 1.99\).
Optimizing with the Derivative
An optimization problem typically requires you to find the value of an endogenous variable (or variables) that maximizes or minimizes a particular objective function. We can use derivatives to find the optimal solution. This is called an analytical approach.
If we draw tangent lines at each value of x in Figure 3.6, only one would be horizontal (with derivative and slope of zero) and that would be the one at the top. This gives us a solution strategy: to find the maximum, find the value of x with the flat tangent line. This is equivalent to finding the value of x where the derivative is zero.
By solving for the value of x where \(\frac{dy}{dx} = 0\), we find the optimal solution. For \(y = 4x - x^2\), this is easy. We set the derivative equal to zero and solve for \(x\mbox{*}\). \[\frac{dy}{dx} = 4 - 2x\mbox{*} = 0\\ 4 = 2x\mbox{*}\\ x\mbox{*} = 2\] The equation that you make when you set the first derivative equal to zero is called the first-order condition. The first-order condition is different from the derivative because the derivative by itself is not equal to anythingyou can plug in any value of x and the derivative expression will pump out an answer that tells you whether and by how much the function is rising or falling at that point. The first-order condition is a special situation in which you are using the derivative to find a horizontal tangent line to figure out where the function has a flat spot.
A reduced form is the answer that you get when the derivative is set equal to zero and solved for the optimal solution. It may be a number or a function of exogenous variables. It cannot have any endogenous variables in the expression. Sometimes, you cannot solve explicitly for \(x\mbox{*}\). We say there is no closed form solution in these cases. The solution may exist (and numerical methods may be used to find it), but we cannot express the answer as an equation.
The second derivative is the derivative of the first derivative. It tells you the slope of the slope function. For example, if a function has a constant slope, we saw that its first derivative is a constant value (like 3 in the first example above). Then the second derivative is zero.
Second derivatives are useful in optimization for the following reason: when you find the value of the endogenous variable that makes the first derivative equal to zero, the point that you have located could be either a maximum or a minimum. If you want to be sure which one you have found, you can check the second derivative. For \(y = 4x - x^2\), the first derivative is \(4 - 2x\) and the second derivative is, therefore, -2. Because the second derivative is negative, we know that our flat spot at x = 2 is a maximum and not a minimum.
In this book, we will not use second derivatives to check that our solutions are truly maxima or minima. Our functions will be (mostly) well behaved and we will focus on the economics of the problem, not the mathematics.
In summary, derivatives are used to measure the rate of change of a function based on a vanishingly small change in x. If we set a derivative equal to zero, we are trying to find an optimal solution by finding a value for x where the tangent line is flat. This solution strategy is based on the idea that a point where the tangent line is horizontal must mean that we are at the top of the function (or bottom, if we are minimizing).
Useful Math Facts
This appendix concludes with a short list of common rules for taking derivatives and working with exponents. The idea here is to sharpen your math skills so you can solve optimization problems analytically.
A derivative can be computed by directly applying the definitioni.e., taking the limit of the change in x as it approaches zero and determining the change in y. Fortunately, however, there is an easier way. Differentiation rules have been developed that make it much less tedious to take a derivative. Most calculus books have inside covers that are full of rules. Many students never grasp that these rules are actually shortcuts. Here is a short list, with special emphasis on those used in economics.
The derivative rules are followed by a few algebra rules relating to legal operations on exponents. We will use these rules often to find optimal solutions and reduce complicated expressions to simpler final answers.
Reading these equations is boring and tedious, but may save a lot of time and effort in the future (especially if your math is rusty). You should consider writing out the examples for a different number, say 6. So, instead of \(x^4\), what is the derivative with respect to x for \(x^6\)?
Derivative Rules
Let x be the variable and a be a constant.
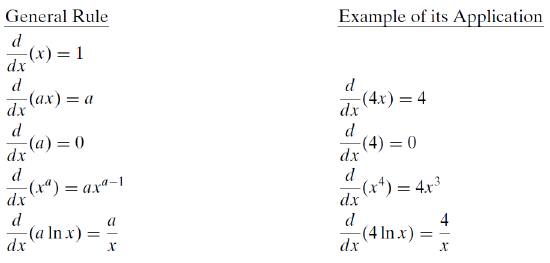
When you take a derivative of a function with respect to a variable, you apply the rules to the different parts of the function. For example, if \(y = 4x - x^2\), then you apply the \(\frac{d}{dx}(ax) = a\) rule to \(4x\), getting 4. You apply the \(\frac{d}{dx}(x^a) = ax^{a-1}\) rule to \(- x^2\) and get \(- 2x\). Thus, the derivative of y with respect to x is \(\frac{dy}{dx} = 4 - 2x\).
There are other calculus rules, of course, such as the chain rule, but we will explain them when they are needed.
Laws of Exponents