8.1.4: Analogical Arguments
- Page ID
- 91192
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When I strike a match it will produce a flame. It is natural to take the striking of the match as the cause that produces the effect of a flame. But what if the matchbook is wet? Or what if I happen to be in a vacuum in which there is no oxygen (such as in outer space)? If either of those things is the case, then the striking of the match will not produce a flame. So it isn’t simply the striking of the match that produces the flame, but a combination of the striking of the match together with a number of other conditions that must be in place in order for the striking of the match to create a flame. Which of those conditions we call the “cause” depends in part on the context. Suppose that I’m in outer space striking a match (suppose I’m wearing a space suit that supplies me with oxygen but that I’m striking the match in space, where there is no oxygen). I continuously strike it but no flame appears (of course). But then someone (also in a space suit) brings out a can of compressed oxygen that they spray on the match while I strike it. All of a sudden a flame is produced. In this context, it looks like it is the spraying of oxygen that causes flame, not the striking of the match. Just as in the case of the striking of the match, any cause is more complex than just a simple event that produces some other event. Rather, there are always multiple conditions that must be in place for any cause to occur. These conditions are called background conditions. That said, we often take for granted the background conditions in normal contexts and just refer to one particular event as the cause. Thus, we call the striking of the match the cause of the flame. We don’t go on to specify all the other conditions that conspired to create the flame (such as the presence of oxygen and the absence of water). But this is more for convenience than correctness. For just about any cause, there are a number of conditions that must be in place in order for the effect to occur. These are called necessary conditions (recall the discussion of necessary and sufficient conditions from chapter 2, section 2.7). For example, a necessary condition of the match lighting is that there is oxygen present. A necessary condition of a car running is that there is gas in the tank. We can use necessary conditions to diagnose what has gone wrong in cases of malfunction. That is, we can consider each condition in turn in order to determine what caused the malfunction. For example, if the match doesn’t light, we can check to see whether the matches are wet. If we find that the matches are wet then we can explain the lack of the flame by saying something like, “dropping the matches in the water caused the matches not to light.” In contrast, a sufficient condition is one which if present will always bring about the effect. For example, a person being fed through an operating wood chipper is sufficient for causing that person’s death (as was the fate of Steve Buscemi’s character in the movie Fargo). Because the natural world functions in accordance with natural laws (such as the laws of physics), causes can be generalized. For example, any object near the surface of the earth will fall towards the earth at 9.8 m/s2 unless impeded by some contrary force (such as the propulsion of a rocket). This generalization applies to apples, rocks, people, wood chippers and every other object. Such causal generalizations are often parts of explanations. For example, we can explain why the airplane crashed to the ground by citing the causal generalization that all unsupported objects fall to the ground and by noting that the airplane had lost any method of propelling itself because the engines had died. So we invoke the causal generalization in explaining why the airplane crashed. Causal generalizations have a particular form:
For any x, if x has the feature(s) F, then x has the feature G
For example:
For any human, if that human has been fed through an operating wood chipper, then that human is dead.
For any engine, if that engine has no fuel, then that engine will not operate.
For any object near the surface of the earth, if that object is unsupported and not impeded by some contrary force, then that object will fall towards the earth at 9.8 m/s2.
Being able to determine when causal generalizations are true is an important part of becoming a critical thinker. Since in both scientific and every day contexts we rely on causal generalizations in explaining and understanding our world, the ability to assess when a causal generalization is true is an important skill. For example, suppose that we are trying to figure out what causes our dog, Charlie, to have seizures. To simplify, let’s suppose that we have a set of potential candidates for what causes his seizures. It could be either:
- eating human food,
- the shampoo we use to wash him,
- his flea treatment,
- not eating at regular intervals,
or some combination of these things. Suppose we keep a log of when these things occur each day and when his seizures (S) occur. In the table below, I will represent the absence of the feature by a negation. So in the table below, “~A” represents that Charlie did not eat human food on that day; “~B” represents that he did not get a bath and shampoo that day; “~S” represents that he did not have a seizure that day. In contrast, “B” represents that he did have a bath and shampoo, whereas “C” represents that he was given a flea treatment that day. Here is how the log looks:
| Day 1 | ~A | B | C | D | S |
|---|---|---|---|---|---|
| Day 2 | A | ~B | C | D | ~S |
| Day 3 | A | B | ~C | D | ~S |
| Day 4 | A | B | C | ~D | S |
| Day 5 | A | B | ~C | D | ~S |
| Day 6 | A | ~B | C | D | ~S |
How can we use this information to determine what might be causing Charlie to have seizures? The first thing we’d want to know is what feature is present every time he has a seizure. This would be a necessary (but not sufficient) condition. And that can tell us something important about the cause. The necessary condition test says that any candidate feature (here A, B, C, or D) that is absent when the target feature (S) is present is eliminated as a possible necessary condition of S.3 In the table above, A is absent when S is present, so A can’t be a necessary condition (i.e., day 1). D is also absent when S is present (day 4) so D can’t be a necessary condition either. In contrast, B is never absent when S is present—that is every time S is present, B is also present. That means B is a necessary condition, based on the data that we have gathered so far. The same applies to C since it is never absent when S is present. Notice that there are times when both B and C are absent, but on those days the target feature (S) is absent as well, so it doesn’t matter.
The next thing we’d want to know is which feature is such that every time it is present, Charlie has a seizure. The test that is relevant to determining this is called the sufficient condition test. The sufficient condition test says that any candidate that is present when the target feature (S) is absent is eliminated as a possible sufficient condition of S. In the table above, we can see that no one candidate feature is a sufficient condition for causing the seizures since for each candidate (A, B, C, D) there is a case (i.e. day) where it is present but that no seizure occurred. Although no one feature is sufficient for causing the seizures (according to the data we have gathered so far), it is still possible that certain features are jointly sufficient. Two candidate features are jointly sufficient for a target feature if and only if there is no case in which both candidates are present and yet the target is absent. Applying this test, we can see that B and C are jointly sufficient for the target feature since any time both are present, the target feature is always present. Thus, from the data we have gathered so far, we can say that the likely cause of Charlie’s seizures are when we both give him a bath and then follow that bath up with a flea treatment. Every time those two things occur, he has a seizure (sufficient condition); and every time he has a seizure, those two things occur (necessary condition). Thus, the data gathered so far supports the following causal conditional:
Any time Charlie is given a shampoo bath and a flea treatment, he has a seizure.
Although in the above case, the necessary and sufficient conditions were the same, this needn’t always be the case. Sometimes sufficient conditions are not necessary conditions. For example, being fed through a wood chipper is a sufficient condition for death, but it certainly isn’t necessary! (Lot’s of people die without being fed through a wood chipper, so it can’t be a necessary condition of dying.) In any case, determining necessary and sufficient conditions is a key part of determining a cause.
When analyzing data to find a cause it is important that we rigorously test each candidate. Here is an example to illustrate rigorous testing. Suppose that on every day we collected data about Charlie he ate human food but that on none of the days was he given a bath and shampoo, as the table below indicates.
| Day 1 | A | ~B | C | D | ~S |
|---|---|---|---|---|---|
| Day 2 | A | ~B | C | D | ~S |
| Day 3 | A | ~B | ~C | D | ~S |
| Day 4 | A | ~B | C | ~D | S |
| Day 5 | A | ~B | ~C | D | ~S |
| Day 6 | A | ~B | C | D | S |
Given this data, A trivially passes the necessary condition test since it is always present (thus, there can never be a case where A is absent when S is present). However, in order to rigorously test A as a necessary condition, we have to look for cases in which A is not present and then see if our target condition S is present. We have rigorously tested A as a necessary condition only if we have collected data in which A was not present. Otherwise, we don’t really know whether A is a necessary condition. Similarly, B trivially passes the sufficient condition test since it is never present (thus, there can never be a case where B is present but S is absent). However, in order to rigorously test B as a sufficient condition, we have to look for cases in which B is present and then see if our target condition S is absent. We have rigorously tested B as a sufficient condition only if we have collected data in which B is present. Otherwise, we don’t really know whether B is a sufficient condition or not.
In rigorous testing, we are actively looking for (or trying to create) situations in which a candidate feature fails one of the tests. That is why when rigorously testing a candidate for the necessary condition test, we must seek out cases in which the candidate is not present, whereas when rigorously testing a candidate for the sufficient condition test, we must seek out cases in which the candidate is present. In the example above, A is not rigorously tested as a necessary condition and B is not rigorously tested as a sufficient condition. If we are interested in finding a cause, we should always rigorously test each candidate. This means that we should always have a mix of different situations where the candidates and targets are sometimes present and sometimes absent.
The necessary and sufficient conditions tests can be applied when features of the environment are wholly present or wholly absent. However, in situations where features of the environment are always present in some degree, these tests will not work (since there will never be cases where the features are absent and so rigorous testing cannot be applied). For example, suppose we are trying to figure out whether CO2 is a contributing cause to higher global temperatures. In this case, we can’t very well look for cases in which CO2 is present but high global temperatures aren’t (sufficient condition test), since CO2 and high temperatures are always present to some degree. Nor can we look for cases in which CO2 is absent when high global temperatures are present (necessary condition test), since, again, CO2 and high global temperatures are always present to some degree. Rather, we must use a different method, the method that J.S. Mill called the method of concomitant variation. In concomitant variation we look for how things vary vis-à-vis each other. For example, if we see that as CO2 levels rise, global temperatures also rise, then this is evidence that CO2 and higher temperatures are positively correlated. When two things are positively correlated, as one increases, the other also increases at a similar rate (or as one decreases, the other decreases at a similar rate). In contrast, when two things are negatively correlated, as one increases, the other decreases at similar rate (or vice versa). For example, if as a police department increased the number of police officers on the street, the number of crimes reported decreases, then number of police on the street and number of crimes reported would be negative correlated. In each of these examples, we may think we can directly infer the cause from the correlation—the rising CO2 levels are causing the rising global temperatures and the increasing number of police on the street is causing the crime rate to drop. However, we cannot directly infer causation from correlation. Correlation is not causation. If A and B are positively correlated, then there are four distinct possibilities regarding what the cause is:
- A is the cause of B
- B is the cause of A
- Some third thing, C, is the cause of both A and B increasing
- The correlation is accidental
In order to infer what causes what in a correlation, we must rely on our general background knowledge (i.e., things we know to be true about the world), our scientific knowledge, and possibly further scientific testing. For example, in the global warming case, there is no scientific theory that explains how rising global temperatures could cause rising levels of CO2 but there is a scientific theory that enables us to understand how rising levels of CO2 could increase average global temperatures. This knowledge makes it plausible to infer that the rising CO2 levels are causing the rising average global temperatures. In the police/crime case, drawing on our background knowledge we can easily come up with an inference to the best explanation argument for why increased police presence on the streets would lower the crime rate—the more police on the street, the harder it is for criminals to get away with crimes because there are fewer places where those crimes could take place without the criminal being caught. Since criminals don’t want to risk getting caught when they commit a crime, seeing more police around will make them less likely to commit a crime. In contrast, there is no good explanation for why decreased crime would cause there to be more police on the street. In fact, it would seem to be just the opposite: if the crime rate is low, the city should cut back, or at least remain stable, on the number of police officers and put those resources somewhere else. This makes it plausible to infer that it is the increased police officers on the street that is causing the decrease in crime.
Sometimes two things can be correlated without either one causing the other. Rather, some third thing is causing them both. For example, suppose that Bob discovers a correlation between waking up with all his clothes on and waking up with a headache. Bob might try to infer that sleeping with all his clothes on causes headaches, but there is probably a better explanation than that. It is more likely that Bob’s drinking too much the night before caused him to pass out in his bed with all his clothes on, as well as his headache. In this scenario, Bob’s inebriation is the common cause of both his headache and his clothes being on in bed.
Sometimes correlations are merely accidental, meaning that there is no causal relationship between them at all. For example, Tyler Vigen4 reports that the per capita consumption of cheese in the U.S. correlates with the number of people who die by becoming entangled in their bedsheets:
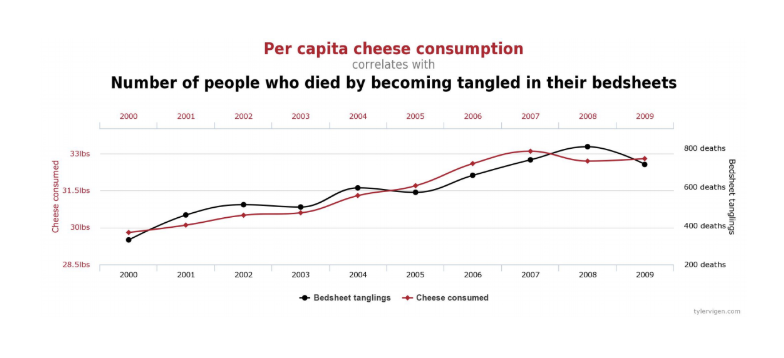
And the number of Mexican lemons imported to the U.S. correlates with the number of traffic fatalities5:
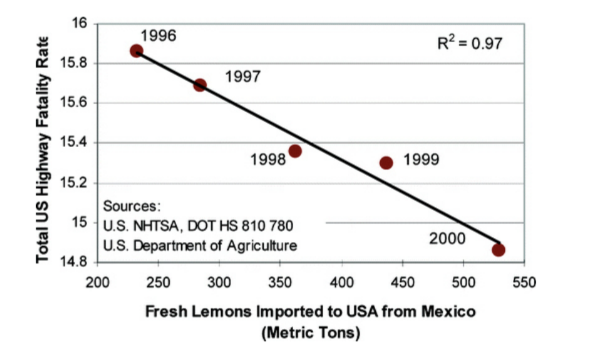
Clearly neither of these correlations are causally related at all—they are accidental correlations. What makes them accidental is that we have no theory that would make sense of how they could be causally related. This just goes to show that it isn’t simply the correlation that allows us to infer a cause, but, rather, some additional background theory, scientific theory, or other evidence that establishes one thing as causing another. We can explain the relationship between correlation and causation using the concepts of necessary and sufficient conditions (first introduced in chapter 2): correlation is a necessary condition for causation, but it is not a sufficient condition for causation.
Our discussion of causes has shown that we cannot say that just because A precedes B or is correlated with B, that A caused B. To claim that since A precedes or correlates with B, A must therefore be the cause of B is to commit what is called the false cause fallacy. The false cause fallacy is sometimes called the “post hoc” fallacy. “Post hoc” is short for the Latin phrase, “post hoc ergo propter hoc,” which means “before this therefore because of this.” As we’ve seen, false cause fallacies occur any time someone assumes that two events that are correlated must be in a causal relationship, or that since one event precedes another, it must cause the other. To avoid the false cause fallacy, one must look more carefully into the relationship between A and B to determine whether there is a true cause or just a common cause or accidental correlation. Common causes and accidental correlations are more common than one might think.
Exercise
Determine which of the candidates (A, B, C, D) in the following examples pass the necessary condition test or the sufficient condition test relative to the target (G). In addition, note whether there are any candidates that aren’t rigorously tested as either necessary or sufficient conditions.
1.
| Case 1 | A | B | ~C | D | ~G |
| Case 2 | ~A | B | C | D | G |
| Case 3 | A | ~B | C | D | G |
2.
| Case 1 | A | B | C | D | G |
| Case 2 | ~A | B | ~C | D | ~G |
| Case 3 | A | ~B | C | ~D | G |
3.
| Case 1 | A | B | C | D | G |
| Case 2 | ~A | B | C | D | G |
| Case 3 | A | ~B | C | D | G |
4.
| Case 1 | A | B | C | D | ~G |
| Case 2 | ~A | B | C | D | G |
| Case 3 | A | ~B | C | ~G | ~G |
5.
| Case 1 | A | B | C | D | ~G |
| Case 2 | ~A | B | C | D | G |
| Case 3 | A | ~B | C | ~D | ~G |
6.
| Case 1 | A | B | ~C | D | ~G |
| Case 2 | ~A | B | C | D | ~G |
| Case 3 | A | ~B | ~C | ~D | G |
7.
| Case 1 | A | B | ~C | D | G |
| Case 2 | ~A | ~B | C | D | ~G |
| Case 3 | A | ~B | C | ~D | ~G |
8.
| Case 1 | A | B | ~C | D | ~G |
| Case 2 | ~A | ~B | ~C | D | ~G |
| Case 3 | A | ~B | ~C | ~D | ~G |
9.
| Case 1 | A | B | ~C | D | G |
| Case 2 | ~A | ~B | C | D | G |
| Case 3 | A | ~B | ~C | D | ~G |
10.
| Case 1 | ~A | B | ~C | D | ~G |
| Case 2 | ~A | B | C | D | G |
| Case 3 | ~A | ~B | ~C | D | G |
For each of the following correlations, use your background knowledge to determine whether A causes B, B causes A, a common cause C is the cause of both A and B, or the correlations is accidental.
1. There is a positive correlation between U.S. spending on science, space, and technology (A) and suicides by hanging, strangulation, and suffocation (B).
2. There is a positive correlation between our dog Charlie’s weight (A) and the amount of time we spend away from home (B). That is, the more time we spend away from home, the heavier Charlie gets (and the more we are at home, the lighter Charlie is.
3. The height of the tree in our front yard (A) positively correlates with the height of the shrub in our backyard (B).
4. There is a negative correlation between the number of suicide bombings in the U.S. (A) and the number of hairs on a particular U.S President’s head (B).
5. There is a high positive correlation between the number of fire engines in a particular borough of New York Cite (A) and the number of fires that occur there (B).
6. At one point in history, there was a negative correlation between the number of mules in the state (A) and the salaries paid to professors at the state university (B). That is, the more mules, the lower the professors’ salaries.
7. There is a strong positive correlation between the number of traffic accidents on a particular highway (A) and the number of billboards featuring scantily-clad models (B).
8. The girth of an adult’s waist (A) is negatively correlated with the height of their vertical leap (B).
9. Olympic marathon times (A) are positively correlated with the temperature during the marathon (B). That is, the more time it takes an Olympic marathoner to complete the race, the higher the temperature.
10.The number gray hairs on an individual’s head (A) is positively correlated with the number of children or grandchildren they have (B).
3 This discussion draws heavily on chapter 10, pp. 220-224 of Sinnott-Armstrong and Fogelin’s
Understanding Arguments, 9th edition (Cengage Learning).
4 http://tylervigen.com/spurious-correlations
5 Stephen R. Johnson, The Trouble with QSAR (or How I Learned To Stop Worrying and Embrace
Fallacy). J. Chem. Inf. Model., 2008, 48 (1), pp. 25–26.


