Marginal Analysis

1.0 Introduction

Economics is the study of human decision-making and the allocation of scarce resources among competing ends. The choice to use more scarce resources to undertake an activity is made at the margin. For example, when allocating your time to study for an exam, you may decide to allocate an hour, initially. If you feel more time is needed to understand the material after an hour has passed, you may decide to study for an additional hour. These study decisions are made on the margin. On the margin, refers to the additional resources needed to make a choice, complete an activity, or take an action. The designated hour to study and the additional hour for studying are marginal decisions. Thinking on the margin is essential in understanding the impact of each additional resource consumed, sold, or gained. It is key to thinking like an economist! Foundational to a thorough understanding of economics is the idea of marginal analysis. This type of analysis is crucial in making informed decisions as a producer or consumer in any market. Marginal analysis is used to compare the additional benefits of an activity to the additional costs incurred by the same activity to meet specified objectives.

Marginal analysis comes into many of the decisions we make. Weighing the additional benefits and costs of making a decision is something that is experienced by everyone. This is the essence of marginal analysis! Whether you realize it or not, marginal analysis is something you do every single day, from deciding to eat that last slice of pizza to pushing yourself through one last rep on the bench with those heavy weights. We undertake marginal analysis in deciding whether or not to go to class each day, by deciding which is more essential at that given moment; another nap, lunch with your friends, a quick run, or learning the class material.

In addition to explicitly considering other alternatives, another benefit of learning marginal analysis more formally is learning you do not need to make decisions by starting from the beginning. Let's go back to the studying example. If you’ve been studying for an exam for 2 hours for your principles of economics course and you’re weighing the decision of whether or not to study for another hour, you are utilizing marginal analysis. We don’t decide every single hour whether or not we should study at all! Consider another example involving farmers, who use the same sort of logic. Assume a farmer is contemplating deciding to invest in more land for their farm. The farmer doesn’t evaluate whether or not it would be profitable to farm their entire operation with the acquisition of the new land. The costs, revenues, and profit for the land the farmer already owns are known. It is the additional (or marginal) costs and revenues incurred by incorporating the new land into the farming operation that they would be concerned with.

The purpose of this chapter is to introduce you to the concept of marginal analysis, present different marginal concepts often used in economics, and begin to present to you how to think "on the margin". We define what "on the margin" means and alternative marginal concepts in the next section. In Section 3, we learn about marginal analysis and different techniques used to conduct marginal analysis. Finally, in Section 4, we present three case studies that apply the concepts and approaches used in the chapter to examine profit maximization for a firm, a problem of pollution abatement in the area of environmental economics, and an application of partial budgeting to the adoption of conservation practices on-farm.

1.1 Learning Objectives

At the end of this chapter you should be able to:

(1) Define what "on the margin" means and identify alternative marginal concepts in economics;

(2) Calculate marginal values for different economic decision situations (e.g. for consuming and producing goods and services); and

(3) Conduct marginal analysis using optimization rules and partial budgeting.

Throughout the chapter, there are many examples to illustrate the concepts we talk about and the case studies will provide in-depth examples that will allow you to walk through situations of calculating marginal values and conducting marginal analysis.

2.0 "On the Margin"

Tractor Production Line [3]

This section of the chapter will introduce the concept of "on the margin", its importance in economic analysis, and different marginal concepts often used in economics. The notion of "on the margin" is central to thinking like an economist.

2.1 What do “on the margin” and marginal mean?

The term marginal is used by economists to describe the additional benefits and costs incurred when one more unit or level of an activity or choice is made. For example, this could be eating one more piece of pizza, producing one more tractor, or studying for one more hour. Benefits and costs can include how "full" you feel, an increase in production costs, or your performance on an exam. “On the margin” is essentially a description of the change that occurs when the amount or level of a choice or activity is being changed incrementally. The marginal change is measured as the additional benefit or cost from the change in the amount or level of an activity or choice.

Marginal changes in economics are often illustrated as the change in the benefits or costs with a one-unit change in the amount or level of a choice or activity being undertaken. For example, consider a government deciding whether or not to build an additional nuclear power plant in their country. The capital required for this kind of decision usually only allows for a single unit of the good to be considered at a time. Marginal changes do not have to be in one-unit increments though. Consider the production of lollipops, which a candy producer may produce in the hundreds of thousands of units. Asking the question “Should I produce one more lollipop?” may seem ludicrous. However, the company may be interested in the marginal decision to open an additional production line to produce 100,000 lollipops and want to know what the additional or marginal cost would be of that decision. Thus, "on the margin" refers to the additional or incremental decrease or increase in benefits or costs from making an incremental change (i.e. one unit change) in a choice or activity. We will explore multiple marginal concepts in this chapter and examine how decisions can be made "on the margin" using marginal analysis.

2.2 Aspects of Thinking "On the Margin"

Marginal analysis is a fundamental and important economic concept that is used in explaining how individuals and entities make decisions. There are a few key aspects encompassing marginal analysis that are important to take into consideration. Understanding the difference between average and marginal concepts, as well as understanding the properties of curves used in marginal analysis are important and will come up in this chapter.

2.3 Marginal Concepts Used in Economics

Marginal analysis can be applied to nearly every single decision we make, but it is perhaps most useful when we can quantify the marginal benefits and marginal costs under consideration. This subsection examines different marginal concepts used in economics, which include marginal concepts related to production, profit, revenue, utility, amongst others. It is important to emphasize that, marginal benefits and marginal costs will be dependent on the situation or decision under consideration, but the concepts here can be useful for decision-making in a number of different contexts.

3.0 Marginal Analysis

This section of the chapter examines how to use the marginal concepts presented in the previous section to conduct marginal analysis. Recall from earlier in the chapter, that marginal analysis is used to compare the additional benefits of an activity to the additional costs incurred by the same activity to meet specified objectives. We will examine two approaches often used in economics to conduct marginal analysis. The first is based on optimization rules and the second is partial budgeting.

3.1 Marginal Benefit (MB) versus Marginal Cost (MC)

Profit or Not [8]

Economists recommend that individuals, firms, and/or organizations consider both the positive attributes or marginal benefits (MB) and negative attributes or marginal costs (MC) of decisions or choices they are faced with. Such consideration means weighing the marginal benefits against the marginal costs of that choice or decision. Individuals and firms should consider all relevant benefits and costs, whether they directly or indirectly impact the individual or firm. Even when an individual or entity has an opportunity to largely benefit directly without much internal cost, there can be externalities involved. Externalities are impacting third parties who do not have direct involvement in the choice, decision, or action being taken. Externalities can be positive and negative, meaning other external benefits and costs may result from a given choice or decision, which should also be considered. In addition, decision-makers want to take account of opportunity costs or the next best thing they could do with the resources they are using for the decision or choice being made.

Thus, all relevant additional benefits and costs of a choice or decision should be considered by individuals, firms, and organizations in their decision-making processes. To help guide these decisions, economists will often employ optimization rules. Optimization rules can be mathematically derived from optimization-type problems, such as firms trying to maximize profit or minimize cost when producing their goods and services, but these derivations are well beyond the scope of this chapter.

In this subsection, we will focus on a general rule for comparing \(MB\) and \(MC\). An individual, firm, or organization should consider enacting a choice or decision as long as the marginal benefits outweigh the marginal costs. Mathematically, this can be represented as: \[MB>=MC\]

That is, if the marginal benefits are greater than or equal to the marginal costs of the choice or decision then an individual, firm, or organization should, from an economic perspective, make that choice or decision.

To explore this consider the following situation: You have to make an effort each morning to go to class during the week. Pick one weekday this coming week. Now consider the following questions.

The optimization rules considered in the next two subsections will be based on this general optimization rule but will allow for the numerical computation of \(MB\) and \(MC\).

3.2 Profit Maximization

In economics, we often assume that firms are profit maximizers. The assumption can be justified by the fact that firms must earn profit to remain in business. However, it is important to recognize that this may not be the firm's only objective. Other motives that drive firms include minimizing risk, cost minimization, promoting environmental sustainability, and charity.

The assumption of profit maximization provides for a relatively strong optimization rule for production decisions made by firms. That is, can a profit-maximizing rule be determined that helps a firm decide how much to produce in the short-run? First, let's present the rule and then we will discuss it. A firm will maximize profit in the short-run by producing up to the point where (1) marginal revenue (\(MR\)) equals marginal cost (\(MC\)), and (2) marginal cost cuts marginal revenue from below.

The second condition helps to make sure that the firm gets through the initial phase of production where marginal profits may be negative. That is, firms may have high fixed costs, which can result in significantly higher marginal costs at the start of production that only begin to decrease as production increases (i.e. as average fixed costs decline). Thus, marginal profit \((MR-MC)\) at the beginning or in the initial stages of production may be negative, but will likely become positive as the level of production increases (as seen in the example with AGSPI in section 2.3.5). So in the initial stages of production, a firm will try to produce until \(Marginal Profit>0\). (If the firm is unable to reach a point in the production process where marginal profit is positive, then it will have to shut down and stop production.)

Now let's turn our attention to the first and most significant part of this optimization rule for profit maximization, that a firm will produce up to the point where \(MR=MC\). To begin to explain why the above optimization rule works, first remember that for a firm selling a single unit of output, the marginal benefit \(MB)\) is the marginal revenue \((MR)\) or price they receive for selling that unit of output. The marginal cost \((MC)\) of producing the unit of output will be the actual marginal cost in dollars (which includes variable cost, fixed cost and opportunity cost for that unit of output). Marginal profit for the unit is then \(MR-MC\). If a firm is a profit maximizer, then it will produce and sell an additional unit of output if the marginal profit for that unit is greater than or equal to zero, i.e. \[MarginalProfit\ge0\]

Remember, that \(Marginal Profit=MR-MC\), so the above rule, implies that the profit-maximizing firm will want to produce and sell an additional unit of output, if: \[MR-MC\ge0\]

This implies a firm should produce as long as \(MR\ge{MC}\) (i.e. they are still earning money on the additional unit of output being produced).

To dive a bit deeper, assume the firm is at a point of production in the short-run, where marginal profit is positive. The firm wants to determine the level of output to produce that will maximize its total profit. As long as marginal profit is positive, total profit will increase. It is only when marginal profit becomes negative that the firm will stop increasing production, as total profit will decrease. Thus, the firm will want to produce as long as the marginal profit is positive, but not when the marginal profit is negative. This condition suggests the firm will want to produce up to the point where \(Marginal Profit=0\). At this point, the firm is making no additional profit from producing more output. That is, the additional profit from the next unit of output is zero. If they go past this point in the production process, marginal profit will become negative, decreasing total profit. Given that \({Marginal Profit}=MR-MC\), a profit-maximizing firm should produce up to the point where \(MR-MC=0\) or: \[MR=MC\]

which is our optimization rule given by (1). The profit-maximizing optimization rule can be applied to many types of firms in many types of markets.

Let us return to the AGSPI example previously explored, considering the production of agricultural drones. The table below provides information about Total Cost, Total Revenue, Marginal Cost, Marginal Revenue, and Marginal Profit for different levels of output (or production) for AGSPI. Now let's use this information to apply the profit maximization rule.

Type caption for table (optional)

We already had you explore in section 2.3.5 how many drones AGSPI should produce. Let's see if you were correct (see Question 13). Using the profit-maximizing optimization rule for a firm, according to condition (2), AGSPI should produce at least 15 drones, as this is the point where they begin to earn a positive marginal level of profit per drone. Now we turn to condition (1), which states we should produce up to the point where \(MR=MC\) and not beyond (i.e. as long as \(MR\ge{MC}\)). If we look at the table, marginal profit remains positive up to the production of 35 drones. At this point \(MR>MC\). If AGSPI produces 40 drones, then marginal profit becomes negative, reducing total profit, because \(MR>MC\). While in the table we do not have a level of production given where \(MR=MC\), we want to make sure we do not choose a level of production past this point where marginal profits become negative. In many examples using tables with production, cost, and revenue information, this will likely be the case. Thus, we want to find the highest level of production where \(MR\ge{MC}\) (i.e. marginal revenue is still greater than marginal cost) or marginal profit is positive, which occurs for AGSPI at a production level of 35 drones. Thus, AGSPI's profit-maximizing level of production is 35 drones.

To see an additional example, view the following video below.

Apple Orchard Profit Max Example [9]

Use the video to answer the following two questions.

3.3 Partial Budgeting (Marginal Budgeting)

Farmer Decisions [10]

Making decisions as a manager will often have an impact on the bottom line. Thus, managers must consider the impacts of their decisions on marginal benefits or revenue and marginal cost. Thus, we have to consider how each decision will impact the profitability of our firm or operation. A very useful technique known as partial budgeting exists to aid in the making of these decisions and incorporates many of the marginal concepts we discussed in this chapter. Partial budgeting is a technique that provides a formal way to estimate the expected marginal change in profit from a particular decision for a firm or operation [11]. For example, partial budgeting can be used to assess the impacts of proposed changes in crop rotations or livestock enterprises on a farm or ranch. Partial budgeting can be viewed as a formal way to conduct profitability analysis by allowing for the comparison of multiple decisions or changes in a production system, providing the manager guidance on how to best maximize profit or meet their goals. In addition, if you consider the profitability of the next best alternative not made, then partial budgeting can also provide one way to estimate the opportunity cost of a given decision.

Partial budgets only consider (i) marginal revenues or changes in revenue and (ii) marginal costs or changes in production costs or expenses of a decision, management changes, or technology adoption. Given that we are often in the midst of production or activity when making decisions, aspects of the production situation or activity not affected by the decision being assessed are excluded from the partial budget. The goal of using partial budgeting is to determine if the proposed decision or change will result in a positive marginal change in profitability. The approach “tallies” the net change based on marginal changes in revenues (benefits) and costs [11-12].

In addition to the financial or monetary estimates that can be derived using partial budgets, personal and social factors can also be incorporated. These factors can include level of risk; desire for personal time for leisure and family; workload on employees; equitability; impacts on the environment; and other factors that are difficult to quantify but are important to the overall firm or operation [11]. Personal and social factors are included in the partial budgets as qualitative components and should also be considered in the marginal decision-making process.

To complete a partial budget, a decision-maker can use the following six steps that are adapted from Kay et al. [11] and Bergtold et al. [12]. The steps are as follows:

Step 1: Identify the proposed change in the production system, activity, or operation. For example, on a farm, the proposed change might be to change crop varieties, adopt no-till, or increase herd size. If you are considering multiple changes, then prepare a separate partial budget for each.

Step 2: Positive Marginal Revenue Changes: Record additional revenues (i.e. changes in marginal revenue). List marginal increases in current revenues and/or new revenue sources generated from the decision being considered.

Step 3: Marginal Cost Reductions: Record marginal decreases or reductions in production or other monetary costs (e.g. cost-savings) from the decision being considered.

Step 4: Marginal Cost Increases: Record marginal increases in or new costs from the decision(s) being considered.

Step 5: Reductions in Marginal Revenue: Record marginal decreases or reductions in revenue, as well as lost revenue sources from the decision being considered.

Step 6: Calculate the marginal change in profit (or net return or other objective measure) by subtracting the negative marginal changes (Step 4 and Step 5) from the positive marginal changes (Step 2 and Step 3). If the difference is positive, there is a net economic benefit or marginal gain from adopting the change or making the decision. If the difference is negative, there is a net economic loss or marginal loss. If the marginal change is zero, the decision to adopt the change may be based on the significance of the personal or social factors being considered.

These changes can be put into a partial budgeting form, which is provided below. A case study example illustrating the use of partial budgets will be provided in the case study section of the chapter.

4.0 Case Studies

Marginal analysis can aid in making decisions at both the individual and firm level. This section will provide you with a set of case studies using marginal analysis in a variety of topics and will apply what you have learned in this chapter. An emphasis on understanding the material will be important for these applied problems.

4.1 Profit Maximization in Production from an Input Perspective

The purpose of this case study is to examine profit maximization for a firm but from an input perspective. That is, how much input should the firm apply to maximize output. The optimization rule here is based on the general profit maximization rule for determining the optimal level of output for a firm, producing up to the level of production where \(MR=MC\). For our purposes, in this case study, we will modify this optimization rule for the input perspective. As examined in section 2.3.3, the marginal revenue from the additional use of one unit of input is referred to as the marginal revenue product (\(MRP\)). \(MRP\) will replace \(MR\) in the optimization rule. The additional cost of one unit of input is called the marginal factor cost \((MFC\)) and this will replace \(MC\) in the optimization rule. Thus, for a firm that wants to maximize profit from production from an input perspective, the firm will produce as long as \(MRP\ge{MFC}\) or up to the point or level of production where: \[MRP=MFC\] The logic behind this optimization rule is very similar to that for the output perspective as presented in section 3.2.

Fertilizer Application [13]

The applied example here will examine the economic optimal level of nitrogen fertilizer to apply to maximize return (or profit) for a corn crop being produced by a farmer. The example will utilize corn production data from Debertin [14] with some modifications.

Consider a farmer who is planting corn on a field in the Corn Belt. The farmer is trying to determine how much fertilizer to apply to maximize her profit on that field from corn production. The farmer has worked with her local extension agents at the nearby land grant university to assemble the information in the table below. The first column indicates the potential amount of nitrogen in lbs that can be applied to the corn crop. The second column provides the expected corn yield at the given level of nitrogen. The first two columns represent the expected corn production schedule for the farmer. Each row represents the agronomic and economic effect of applying an additional 20 lbs of nitrogen to the corn crop. The third column provides the marginal product of fertilizer (\(MP_{fertilizer}\)) for each additional pound of fertilizer applied to the corn crop at that level of production. The fourth column is the expected price of corn at harvest. The fifth column is the marginal revenue product from fertilizer application (\(MP_{fertilizer}\)). The fifth column is the marginal factor cost of nitrogen \(MFC\) or the cost of nitrogen per pound, which is assumed to be $0.55 per pound. The last column is the marginal profit from applying an additional pound of nitrogen and is calculated as the \(MRP_{fertilizer}-MFC\). Use this information to answer the following questions. The blanks in the table are left for you to fill in (i.e. on a separate piece of paper).

4.2 Environmental Economics and Pollution Abatement

In economics, market transactions or decisions (e.g. driving to work or planting a crop) may not take account of the full impact of the transaction or decision on society or the environment. That is, individuals and businesses may engage in economic activity (consuming and producing goods and services) without considering the impact this has on the rest of society. If this activity has a negative impact on society or the environment, then we say that this economic activity may result in a negative externality. We define a negative externality as a situation where the parties in the market transaction or decision being considered (through the market price) do not fully account for all the costs of the market activity on society (or third parties), such as health impacts, pollution, etc. [15]. The impact on society or a third party includes potential harm or loss of welfare, which is uncompensated. Of particular interest in this case study is the ability to use marginal analysis in examining the economics of negative externalities. That is, we can use the notions of marginal benefit and marginal cost to examine when it is economically optimal to take account of negative externalities in society. The following video provides additional information on externalities.

Externalities Video [16]

We will use the case of water pollution as our example. Consider a farmer who plants a majority of their peanut crop next to a river. The farmer has not yet adopted conservation practices, such as vegetative or field buffers, that would prevent run-off from their crop field from flowing into the river. The farmer bases their peanut production system on what his parents did in the 1990s, given that his parents earned a good income producing peanuts. The production of peanuts requires a significant application of pesticides that may potentially leach or run-off the field after application into the river and other streams or lakes [17,18]. Downstream is a small town that uses the river for drinking water and recreation (swimming and fishing). Local environmental safety officials have tested the water and found that current water levels contain an unsafe level of pesticides that make it hazardous for residents to use. The local officials have determined that the primary source of the pollution originates from the farmer's peanut field upstream. After consulting with the local town council, they want to try to find a way to encourage the farmer to reduce their use of pesticides or put in conservation measures, such as conservation buffers, to make the water safe again. The conservation buffer, also known as a field buffer or vegetative strip helps to absorb some of the excess pesticides that may run off the field. They decide to look for and consult an environmental economics professor at the local university for an answer.

The environmental economics professor tries to explain the problem from an economic point of view to the local environmental safety officials. She indicates that the decision to reduce pollution to an “economically optimal level” is determined using marginal analysis. She indicates that it is unlikely an optimal solution from a market perspective will eliminate all of the pollution too. She explains that, first, one must consider the marginal benefit of the economic activity undertaken by the farmer. That is, for each unit of pesticide applied to the peanut crop by the farmer, the farmer will earn additional benefit (e.g. from higher crop yields), but it is likely the case that this marginal benefit will decrease as more pesticide is applied due to the Law of Diminishing Marginal Return, (see section 2.3.3 for more information on this concept). Decreasing marginal yields from additional pesticide applications or higher rates means that a farmer is marginally earning less revenue with each additional unit of pesticide applied, assuming crop prices are constant. This change is similar to marginal revenue but is referred to as marginal revenue product \(MRP\) or the marginal change in total revenue from a one-unit change in pesticide use (i.e. \(MRP=\frac{△TR}{△X}\)). Assume the cost of a unit of pesticide is \($W\). Then the marginal cost of a unit of pesticide, known as the marginal factor cost \(MFC\) is \($W\) (i.e. \(MFC=\frac{△TC}{△X}=$W\)).

She goes on to discuss that the concepts in the prior paragraph can now be used to help determine the marginal benefit, or what we will call the marginal net private benefit (\(MNPB\)) to the farmer growing the peanut crop. The marginal net private benefit or \(MNPB\) is in essence the marginal profit from using an additional unit of pesticides or \(MNPB={MRP}-{MFC}\) [19]. Given that \(MRP\) is likely decreasing as more pesticide is applied and \(MFC\) is constant (e.g. \($W\)), then \(MNPB\) will be decreasing, as well. The \(MNPB\) Curve is illustrated in Figure 1. As crop output increases with additional pesticide use, \(MNPB\) decreases. So due to the Law of Diminishing Marginal Returns, \(MNPB\) will be decreasing for the farmer with additional application of pesticides due to less yield from each additional unit of pesticide being applied.

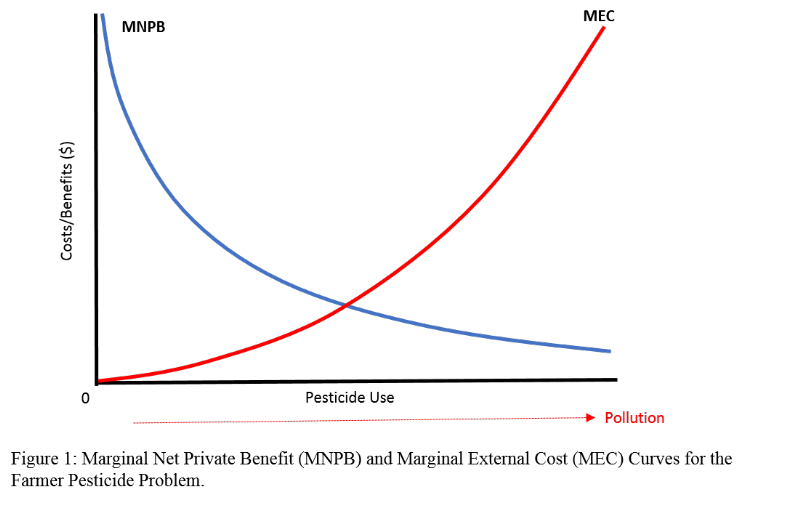
It is important to note that \(MNPB\) does not take into account any costs to society or third parties. These costs, known as negative externalities, are characterized in this example by health impacts and loss of recreation felt along the river downstream. In addition, it is emphasized that there is no direct economic incentive in the market for the farmer to adjust their behavior.

The other curve in Figure 1 is the Marginal External Cost (\(MEC\)) curve [19]. As crop output increases, driven by the increasing use of pesticides by the farmer (holding all else constant), the amount of pesticide leaching or running off the field increases. This type of leaching or run-off that impacts the river and the small town downstream is known as non-point source pollution, as it is usually difficult for environmental safety officials to pinpoint the exact source of the pollution (e.g. the starting point). Thus, as shown in Figure 1, as pesticide use increases, so does the nonpoint source pollution (designated by the red arrow below the X-axis). The increased pollution in the water leads to water quality problems for residents using the water for drinking water and watering livestock, as well as the lost recreational use of the small river due to potential health hazards. These problems can be assigned a monetary cost, which could be equal to actual health costs; the cost of buying bottled water or filters; the cost of lost recreational income from use of the river; etc. We refer to the costs as external costs. These external costs increase with the level of pollution. Each additional unit of pesticide use increases the external cost to society, which we refer to as the marginal external cost, represented by the \(MEC\) curve in Figure 1 [19].

The economist points out that the environment can deal with some level of pollution or waste through natural processes. Thus, it may not be economically optimal to prevent all pollution or eliminate all waste from production processes. So at what point, from an economic point of view, is the optimal level of pollution? This point occurs where \({MNPB}={MEC}\), that is where the marginal net private benefit is equal to the marginal external cost. This occurs where an additional unit of pesticide results in an increase in marginal net private benefit to the farmer equal to the marginal external cost to society (or the citizens of the small town). In this sense, it may be socially optimal to make sure that the gains from private production are not at the expense or greater than the costs to society. This occurs where \({MNPB}={MEC}\). Thus, the optimal level of pollution here may be economically and socially optimal, maximizing the net welfare of society (or all residents of the local community). It should be noted, that there are other ways and criteria used to assess the impacts on society and its welfare, as well.

The condition that \({MNPB}={MEC}\) is an equilibrium condition. That is, from an economic point of view there is not an incentive for society to move away from this point. To see this, consider the following questions that explore what would likely happen if \(MNPB\) was not equal to \(MEC\).

Many conservation programs exist at the local, state, and federal governmental level. For example, the USDA Natural Resource Conservation Service (USDA- NRCS) administers the Environmental Quality Incentives Program (EQIP) to incentivize farmers to adopt and add conservation practices on their farms to improve soil health, reduce soil erosion, improve water quality, sequester carbon, etc. USDA-NRCS incentivizes farmers by offering monetary incentives to adopt conservation practices in their farming operations. (For more information on this program see: https://www.nrcs.usda.gov/wps/portal/nrcs/main/national/programs/financial/eqip/.) One practice that can help to reduce run-off from fields that may result in pesticides getting into water bodies, such as a river, is vegetative or field buffers. USDA-NRCS refers to these as conservation buffers, which they define as: “small areas or strips of land in permanent vegetation, designed to intercept pollutants and manage other environmental concerns” [20].

Consider the situation where the small town decides to incentivize the peanut farmer to install conservation buffers along their fields adjacent to the river and the farmer agrees to do this. Assume there is no net change to \(MNPB\) for the farmer (assuming the cost-share covers the cost of installation). For the small town, for each unit of pesticide applied to the fields adjacent to the river, less pollution now runs-off into the river. This results in lower marginal external costs. Thus, the adoption of conservation practices can help to potentially increase the net benefit of private production to society by potentially reducing external costs to society overall.

4.3 Partial Budgeting and Conservation Adoption

Partial budgeting provides a very organized and formal way of conducting marginal analysis of decisions using monetary values. To illustrate the use of this technique, let’s consider a farming example that is adapted from Bergtold et al. [12]. Farmer Jane farms 600 acres of cotton conventionally in Southeast Kansas. A long-term goal is to move to a conservation tillage system (utilizing no-tillage equipment and management). No-tillage is defined as a crop production system in which seeds are planted into soil that has not been tilled. No-tillage practices are also known as no-till, zero tillage, and direct seeding. No-tillage systems may require equipment modifications and weeds are controlled using herbicides rather than cultivation [21].

No-Till [2]

To assess the transition from a conventional to a no-tillage system, Jane looks for data online and finds studies providing cotton yield differences between conventional and no-tillage production. Jane determines that transitioning to no-tillage from conventional tillage will result in a 60-pound-per-acre increase in cotton yield. After talking with her local farm dealer, she is also able to purchase a slightly used no-till planter costing $15,000. The useful life of the planter is expected to be seven years with a $1,000 salvage value. Jane can take out a loan to purchase the planter with an annual interest rate of 5 percent. Additionally, Jane can determine that repair and insurance rates should be 2 and 2.5 percent, respectively, of the net value of the used planter, $14,000; (the net value is the actual cost minus salvage value). Below is a partial budget chart outlining the partial budgeting analysis for this case study. The cost of the new planter is expected to be $5.63 per acre, which is equal to the interest cost of $1.25 per acre (\(\frac{$15,000\times0.05}{600}\)), plus repair costs of $0.47 per acre (\(\frac{$14,000\times.02}{600}\)), plus insurance costs of $0.58 per acre (\(\frac{$14,000\times0.025}{600}\)), as well as depreciation costs of $3.33 per acre (\(\frac{$15,000-$1000}{7\times600}\)).

Assume that the price of cotton lint (which is the yield from cotton that is sold) is $0.85 per pound.

Converting to no-tillage can help farmers reduce costs by reducing the number of passes made across the field for tillage operations no longer performed (like disking, harrowing, cultivation, plowing, etc.). Let’s assume, that Jane can eliminate two tillage passes (a disking and deep tillage operation) each year on her 600 acres of cotton. The production cost savings is estimated to be $20 per acre. Given that Jane is in southeast Kansas, she wants to further protect and enhance the productivity of the soil in her new no-tillage crop production system, so Jane decides to plant a cover crop at a cost of $25 per acre. Cover crops are crops planted between regular cash crops in rotation to provide mulch to cover the soil, enhance soil fertility, and help suppress weeds. The cover crop is not expected to change cotton yield but will help maintain soil fertility and reduce soil erosion.

Given that cultivation will no longer be used to control weeds in the field, the no-tillage system will require the use of herbicides with additional passes for herbicide applications during the growing season. The expected cost of the additional herbicide applications is $18 per acre, which includes cover crop termination in the spring and weed control during the summer months.

The partial budgeting table below is partially filled out. The questions will guide you through the analysis and filling out of this Table. It could be useful to print out the Table (copy and paste to a word processor) and use it to guide you through the questions.

5.0 Concluding Remarks

In this chapter, we introduced you to the marginal concepts that are central to an economic way of thinking, including marginal benefit, marginal revenue, marginal cost, and marginal profit, among others. These concepts are used in conducting marginal analysis, which can be done using different methods. Two presented here are the use of optimization rules, such as a firm maximizing profit for the production of a single good up to the point where \(MR=MC\) and \(MC\) cuts \(MR\) from below. Another important and useful tool presented was partial budgeting, which is a tool used by many firms and producers today. Finally, you were presented with some case studies to expand on these topics and present how they can be used in analyzing decisions.

6.0 References

[1] Image courtesy through Pixabay, within the public domain. (Grain)

[2] Image courtesy of Wikimedia Commons, under the Creative Commons Attribution-Share Alike 2.0 Generic License (No-till)

[3] Image courtesy of Homoatrox through Wikimedia Commons, under license CC BY-SA 4.

[4] Wikipedia. "∂∂". Available online at: https://en.Wikipedia.org/wiki/%E2%88%82.

[5] Image courtesy of Mydogategodshat through Wikimedia Commons, under license CC BY-SA 3.0.

[6] Image courtesy of barskefrank through Pixabay, under license by Pixabay.

[7] Video courtesy of lostmy1 through Youtube, under license CC BY Attribution 3.0 Unported.

[8] Image courtesy of Kevin Hodgson via Flickr, under license CC BY-SA 2.0

[9] Video courtesy of Saylor Academy via Youtube, under license CC BY Attribution 3.0 Unported.

[10] Image courtesy of Keith Wellner (USDA, Agricultural Research Service) via Free Stock Photos, under license CC0 1.0 Universal.

[11] Kay, R.D., W.M. Edwards and P.A. Duffy. 2004. Farm Management. 5thed. New York: McGraw Hill.

[12] Bergtold, J.S., A. Smith, M. Lamb and L. Duzy. 2019. “Conservation Economics: Budgeting, Cover Crops and Government Programs.” In: Conservation Tillage Systems: Production, Profitability and Stewardship. J. Bergtold and M. Sailus (eds.). USDA-SARE. 2020.

[13] Image courtesy of Lynn Betts and the USDA, Natural Resource Conservation Service via Wikimedia Commons, within the Public Domain.

[14] Debertin, D.L. 1986. Agricultural Production Economics, 2nd ed. Upper Saddle River, NJ: Pearson Education.

[15] Barkley, A. and P.W. Barkley. (2016). Principles of Agricultural Economics. 2nded. New York, NY: Routledge.

[16] Video courtesy of Darin Bell via Youtube, under license CC BY 3.0 Attribution Unported.

[17] Kvien, C.K., A.K. Culbreath, J.W. Wilcut, S.L. Brown and D.K. Bell. (1993). Peanut production in systems restricting use of pesticides based on carcinogenicity and leachability. Peanut Science20: 118 – 124.

[18] Roberson, P. (2009). High-yield, high-quality peanuts. Delta Farm Press. Online. Available at: https://www.farmprogress.com/peanuts/high-yield-high-quality-peanuts. (Accessed 03/29/2019).

[19] Pearce, D.W. and R.K. Turner. (1990). Economics of Natural Resources and the Environment. Baltimore, MD: The Johns Hopkins University Press.

[20] Natural Resource Conservation Service, USDA. Buffer strips: common sense conservation. Online. Available at: https://www.nrcs.usda.gov/wps/portal/nrcs/detail/national/newsroom/features/?cid=nrcs143_023568. Last Accessed: April 5, 2019.

[21] Derpsh, R. “What is No-Till Farming?” NO-Tillage, Sustainable Agriculture in the New Millennium. Available at: http://www.rolf-derpsch.com/en/no-till/what-is-no-till-farming/. Accessed: March 22, 2019.