5.2: Number and Operations

Course Competency 5. Examine strategies that teach early math skills.

5.2. identify concepts of number operations.

Number and Operations

Number and Operations is a part of Number Sense. Strong number sense is highly related to later mathematical development. Both Wisconsin Model Early Learing Standards B.El.1 and B.EL.2 align with Number Sense.

We can think of B.EL. 1 Demonstrates understanding of numbers and counting as the beginning or more basic concepts involved with Number Sense such as imitating counting, rote counting, one-to-one correspondence, and recognizing and writing numerals.

B.EL. 2 Understands number operations and relationships deals with more complex concepts in Number Sense such as comparing quantities, subitizing, more and less, adding (combining sets), and subtraction (removing from sets).

Please see the Wisconsin Model Early Learning Standards for Mathematical Thinking to review the standards, developmental continuum and sample behaviors of adults.

The information below is from the California Preschool Standards and is again provided as a reference to the age you may see these Number and Operations skills appear. However, remember the Wisconsin Model Early Learning Standards include the skills for Number Sense in order of development but do not assign a specific age to any skills as all children develop at their own rate and time.

Examples in 2.0 would correlate to WMELS B.EL. 2 Understands number operations and relationships

At around 48 months of age	At around 60 months of age
2.0 Children begin to understand number relationships and operations in their everyday environment.	2.0 Children expand their understanding of number relationships and operations in their everyday environment.
2.1 Compare visually (with or without counting) two groups of objects that are obviously equal or nonequal and communicate, “more” or “same.”	2.1 Compare, by counting or matching, two groups of up to five objects and communicate, “more,” “same as,” or “fewer” (or “less”).
2.2 Understand that adding to (or taking away) one or more objects from a group will increase (or decrease) the number or objects in the group.	2.2 Understand that adding one or taking away one changes the number in a small group of objects by exactly one.

2.3 Understand that putting two groups of objects together will make a bigger group.	2.3 Understand that putting two groups of objects together will make a bigger group and that a group of objects can be taken apart into smaller groups.
2.4 Solve simple addition and subtraction problems nonverbally (and often verbally) with a very small number of objects (sums up to 4 or 5).	2.4 Solve simple addition and subtraction problems with a small number of objects (sums up to 10), usually by counting.

Supporting the Development of Number and Operations

Ten-Frames

Another way to develop number sense and the more complex skills involved with number and operations in children is to use ten-frames. A “ten-frame” is a rectangle, separated into two rows, with 10 equal spaces. Here is a blank ten-frame from NRICH.

Ten-frames help students develop number sense, a sense of ten, and learn basic number facts. A ten-frame also gives students a visual of numbers, of composing and decomposing numbers, and is a good way to teach addition and subtraction within 10.

This Ten Frame applet from NCTM Illuminations is a fun way for students to practice counting and addition skills.

Hundreds Chart

A Hundreds Chart is essential in every K-2 classroom. Ask students what patterns they see on the Hundreds Chart. You can also begin to “hide” numbers on the Hundreds Chart and ask students to tell what that number is and how they know. See Math, Kids and Chaos to learn what a hundreds chart is and how to use one.

Whole Number Computation

Computational fluency is the ability to accurately, efficiently, and flexibly compute with basic operations (National Research Council, 2001) and is developed over time. In elementary school, students learn about the four basic operations, the properties of the operations, and the strategies to perform those operations. It is developed progressing from concrete models to drawings and then to symbols. The Concrete Representational Abstract (CRA) approach helps students make the connection from concrete manipulatives to abstract mathematical ideas. The three stages of learning mathematics are:

• Concrete – students physically manipulate objects to solve a mathematics problem
• Representational (or semi-concrete) – involves using images to represent objects.
• Abstract (or symbolic) – using only numbers and symbols to solve math problems.

In preschool, we would mostly be working with Concrete and then Representational. Older children would work with Abstract computations once they enter school. However, some children with advanced mathematical abilities may be able to complete abstract or symbolic computations sooner.

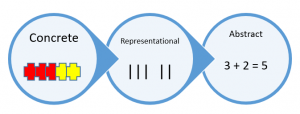
CRA is grounded in the constructivist theory of learning. Teachers begin with concrete manipulatives, transition to visual representations/drawings, and then move to abstract mathematical numbers and symbols. When teaching students addition and subtraction, begin with models/manipulatives, and then progress to bar diagrams, and number lines.

Watch the video from Graham Fletcher, “The Progression of Addition and Subtraction.”

Addition and Subtraction Computation

In kindergarten, students developed an understanding of addition as putting together and adding to, and subtraction as taking apart and taking from. Students in first grade are expected to add two-digit numbers to one-digit numbers; and in second grade, students add two- and three-digit numbers. It is important to note that the traditional algorithms are not required until fourth grade. Therefore, students are expected to compose and decompose numbers and use flexible methods to solve problems.

When adding two or more numbers, the result is the sum. The symbol used for addition is the plus sign (+). The inverse of addition is subtraction, and the result is called the difference. The symbol used for subtraction is the minus sign (-).

First grade students will extend their number facts and place value strategies to add within 100. Do not introduce the traditional addition or subtraction algorithms in first grade. Instead, represent a problem using words, numbers, pictures, manipulatives, and/or symbols.

Estimation

Don’t teach estimation by asking students “make a guess.” The word “estimate” comes from the Latin word aestimare, which means to value. To estimate means to judge the value of something, and an estimate is the resulting calculation. A “guess” is to form an opinion with little or no evidence. When you tell students to make a guess, they are making uninformed conclusions. On the other hand, estimating means to make an informed decision based on data and models (Nichol, n.d.).

Vignettes

The children cleaned up the play yard before going back inside. The teacher, Ms. Denise, had noticed that not all the shovels were picked up from the sandbox. Ms. Denise asked for help saying, “We need all five shovels back in the box so our toys aren’t lost. I see here only three. We need more shovels in the box. How many more shovels do we need?” The teacher had noticed that Ling Wa, one of the older preschool children in the group, was counting her fingers, trying to find out how many shovels were missing.

Ling Wa suddenly said, “Ms. Denise, we need two more.”

Ms. Denise went further, asking, “Do you think we need two more shovels?” How did you figure that out?”