Problem Set 1: Use Elasticities for Exogneous Variables to Estimate Shocks and Changes to an Equilibrium. In this problem set you can assume that it is appropriate to treat W and M as exogenous variables.
Exercise \(\PageIndex{1}\)
Given the following:
\(\phi_{11} = 0.5\)
\(\phi_{1W} = -0.15\)
\(\varepsilon_{11} = -1.5\)
\(\varepsilon_{1M} = -0.5\)
\(\% \Delta M = 6\)
\(\% \Delta W = 0\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S= 0\)
\(\textrm{Demand Shock}: D= -3\)
\(\% \Delta P_{1} = -1.5\)
\( \% \Delta Q_{1} = -0.75\)
Exercise \(\PageIndex{2}\)
Given the following:
\(\phi_{11} = 1.5\)
\(\phi_{1W} = -0.25\)
\(\varepsilon_{11} = -1.75\)
\(\varepsilon_{1M} = 0.5\)
\(\% \Delta M = 5\)
\(\% \Delta W = 3\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S= -0.75\)
\(\textrm{Demand Shock}: D= 2.5\)
\(\% \Delta P_{1} = 1\)
\( \% \Delta Q_{1} = 0.75\)
Exercise \(\PageIndex{3}\)
Given the following:
\(\phi_{11} = 0.5\)
\(\phi_{1W} = -0.3\)
\(\varepsilon_{11} = -2\)
\(\varepsilon_{1M} = -0.4\)
\(\% \Delta M = 8\)
\(\% \Delta W = 0\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S= 0\)
\(\textrm{Demand Shock}: D= -3.2\)
\(\% \Delta P_{1} = -1.28\)
\( \% \Delta Q_{1} = -0.64\)
Exercise \(\PageIndex{4}\)
Given the following:
\(\phi_{11} = 2\)
\(\phi_{1W} = -0.1\)
\(\varepsilon_{11} = -3\)
\(\varepsilon_{1M} = 0.3\)
\(\% \Delta M = 0\)
\(\% \Delta W = 8\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S= -0.8\)
\(\textrm{Demand Shock}: D= 0\)
\(\% \Delta P_{1} = 0.16\)
\( \% \Delta Q_{1} = -0.48\)
Exercise \(\PageIndex{5}\)
Given the following:
\(\phi_{11} = 0.5\)
\(\phi_{1W} = -0.2\)
\(\varepsilon_{11} = -1.5\)
\(\varepsilon_{1M} = 0.4\)
\(\% \Delta M = 5\)
\(\% \Delta W = 4\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S= -0.8\)
\(\textrm{Demand Shock}: D= 2\)
\(\% \Delta P_{1} = 1.4\)
\( \% \Delta Q_{1} = -0.1\)
Exercise \(\PageIndex{6}\)
Given the following:
\(\phi_{11} = 0.25\)
\(\phi_{1W} = -0.3\)
\(\varepsilon_{11} = -1.75\)
\(\varepsilon_{1M} = 0.5\)
\(\% \Delta M = 0\)
\(\% \Delta W = 8\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S= -2.4\)
\(\textrm{Demand Shock}: D= 0\)
\(\% \Delta P_{1} = 1.2\)
\( \% \Delta Q_{1} = -2.1\)
Exercise \(\PageIndex{7}\)
Given the following:
\(\phi_{11} = 1\)
\(\phi_{1W} = -0.5\)
\(\varepsilon_{11} = -2\)
\(\varepsilon_{1M} = -0.5\)
\(\% \Delta M = 5\)
\(\% \Delta W = 8\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S= -4\)
\(\textrm{Demand Shock}: D= -2.5\)
\(\% \Delta P_{1} = 0.5\)
\( \% \Delta Q_{1} = -3.5\)
Exercise \(\PageIndex{8}\)
Given the following:
\(\phi_{11} = 0.5\)
\(\phi_{1W} = -0.7\)
\(\varepsilon_{11} = -3\)
\(\varepsilon_{1M} = 0.4\)
\(\% \Delta M = 0\)
\(\% \Delta W = 2\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S= -1.4\)
\(\textrm{Demand Shock}: D= 0\)
\(\% \Delta P_{1} = 0.4\)
\( \% \Delta Q_{1} = -1.2\)
Exercise \(\PageIndex{9}\)
Given the following:
\(\phi_{11} = 1.5\)
\(\phi_{1W} = -0.5\)
\(\varepsilon_{11} = -1.75\)
\(\varepsilon_{1M} = -0.6\)
\(\% \Delta M = 5\)
\(\% \Delta W = 6\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S= -3\)
\(\textrm{Demand Shock}: D= -3\)
\(\% \Delta P_{1} = 0\)
\( \% \Delta Q_{1} = -3\)
Exercise \(\PageIndex{10}\)
Given the following:
\(\phi_{11} = 0.75\)
\(\phi_{1W} = -0.2\)
\(\varepsilon_{11} = -1.75\)
\(\varepsilon_{1M} = -0.4\)
\(\% \Delta M = 7\)
\(\% \Delta W = 0\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S= 0\)
\(\textrm{Demand Shock}: D= -2.8\)
\(\% \Delta P_{1} = -1.12\)
\( \% \Delta Q_{1} = -0.84\)
Problem Set 2: Use Per Unit Cost or Valuation Estimates to Compute Shocks and Changes to an Equilibrium
Exercise \(\PageIndex{1}\)
Given the following:
\(\phi_{11} = 1.5\)
\(\varepsilon_{11} = -1\)
\(\textrm{Per unit change in production cost is } 8 \%\)
\(\textrm{Per unit change in willingness to pay is } = 3 \%\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S = -12\)
\(\textrm{Demand Shock}: D = 3\)
\(\% \Delta P_{1} = 6\)
\(\% \Delta Q_{1} = -3\)
Exercise \(\PageIndex{2}\)
Given the following:
\(\phi_{11} = 1\)
\(\varepsilon_{11} = -2\)
\(\textrm{Per unit change in production cost is } 0 \%\)
\(\textrm{Per unit change in willingness to pay is } = -6 \%\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S = 0\)
\(\textrm{Demand Shock}: D = -12\)
\(\% \Delta P_{1} = -4\)
\(\% \Delta Q_{1} = -4\)
Exercise \(\PageIndex{3}\)
Given the following:
\(\phi_{11} = 0.5\)
\(\varepsilon_{11} = -2\)
\(\textrm{Per unit change in production cost is } 6 \%\)
\(\textrm{Per unit change in willingness to pay is } = 7 \%\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S = -3\)
\(\textrm{Demand Shock}: D = 14\)
\(\% \Delta P_{1} = 6.8\)
\(\% \Delta Q_{1} = 0.4\)
Exercise \(\PageIndex{4}\)
Given the following:
\(\phi_{11} = 2\)
\(\varepsilon_{11} = -6\)
\(\textrm{Per unit change in production cost is } -2 \%\)
\(\textrm{Per unit change in willingness to pay is } = -3 \%\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S = 4\)
\(\textrm{Demand Shock}: D = -18\)
\(\% \Delta P_{1} = -2.75\)
\(\% \Delta Q_{1} = -1.5\)
Exercise \(\PageIndex{5}\)
Given the following:
\(\phi_{11} = 2\)
\(\varepsilon_{11} = -3\)
\(\textrm{Per unit change in production cost is } 0 \%\)
\(\textrm{Per unit change in willingness to pay is } = 5 \%\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S = 0\)
\(\textrm{Demand Shock}: D = 15\)
\(\% \Delta P_{1} = 3\)
\(\% \Delta Q_{1} = 6\)
Exercise \(\PageIndex{6}\)
Given the following:
\(\phi_{11} = 1.5\)
\(\varepsilon_{11} = -1.75\)
\(\textrm{Per unit change in production cost is } -5 \%\)
\(\textrm{Per unit change in willingness to pay is } = -5 \%\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S = 9\)
\(\textrm{Demand Shock}: D = -10.5\)
\(\% \Delta P_{1} = -6\)
\(\% \Delta Q_{1} = 0\)
Exercise \(\PageIndex{7}\)
Given the following:
\(\phi_{11} = 1\)
\(\varepsilon_{11} = -4\)
\(\textrm{Per unit change in production cost is } -4 \%\)
\(\textrm{Per unit change in willingness to pay is } = 0 \%\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S = 4\)
\(\textrm{Demand Shock}: D = 0\)
\(\% \Delta P_{1} = -0.8\)
\(\% \Delta Q_{1} = 3.2\)
Exercise \(\PageIndex{8}\)
Given the following:
\(\phi_{11} = 2\)
\(\varepsilon_{11} = -3\)
\(\textrm{Per unit change in production cost is } -6 \%\)
\(\textrm{Per unit change in willingness to pay is } = 0 \%\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S = 12\)
\(\textrm{Demand Shock}: D = 0\)
\(\% \Delta P_{1} = -2.4\)
\(\% \Delta Q_{1} = 7.2\)
Exercise \(\PageIndex{9}\)
Given the following:
\(\phi_{11} = 1.5\)
\(\varepsilon_{11} = -1.75\)
\(\textrm{Per unit change in production cost is } 5 \%\)
\(\textrm{Per unit change in willingness to pay is } = 5 \%\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S = -7.5\)
\(\textrm{Demand Shock}: D = 8.75\)
\(\% \Delta P_{1} = 5\)
\(\% \Delta Q_{1} = 0\)
Exercise \(\PageIndex{10}\)
Given the following:
\(\phi_{11} = 0.5\)
\(\varepsilon_{11} = -0.75\)
\(\textrm{Per unit change in production cost is } 6 \%\)
\(\textrm{Per unit change in willingness to pay is } = -7 \%\)
What is the supply shock?
What is the demand shock?
What is the change in equilibrium price?
What is the change in equilibrium quantity?
- Answer
-
\(\textrm{Supply Shock}: S = -3\)
\(\textrm{Demand Shock}: D = -5.25\)
\(\% \Delta P_{1} = -1.8\)
\(\% \Delta Q_{1} = -3.9\)
Problem Set 3: Multiple Choice
Exercise \(\PageIndex{1}\)
- Which best describes a market equilibrium?
a) A price such that quantity supplied equals quantity demanded.
b) The confluence of exogenous factors that alter conditions within the market in question.
c) Forces that cause changes in price and or quantity in a market.
d) A situation where prices reach what many consider to be reasonable levels. For instance, the market for gasoline has finally returned to an equilibrium after several years of high prices.
- Answer
-
a
Exercise \(\PageIndex{2}\)
- In equilibrium models, endogenous variables
a) Are variables that cause shifts in the demand and supply curves.
b) Are prices and quantities in the markets being analyzed.
c) Are non-existent because all variables are exogenous in these models.
d) Are difficult to measure but still affect the equilibrium (e.g., changes in preferences).
- Answer
-
b
Exercise \(\PageIndex{3}\)
- If you are modeling a market equilibrium and you need to account for feedback from other markets or sectors of the economy then you should be using
a) A partial equilibrium model.
b) A feedback accountability model.
c) A general equilibrium model.
d) A model that forces cross-price elasticities to be negative.
- Answer
-
c
Exercise \(\PageIndex{4}\)
- Consider a single market. Which would be most likely to cause an increase in both the equilibrium price and the equilibrium quantity?
a) A positive supply shock
b) A decrease in consumer incomes, assuming demand is for an inferior good
c) A decrease in consumer incomes, assuming demand is for a normal good
d) A negative supply shock
- Answer
-
b
Use the scenario below to answer questions 5 - 8.
Two products are substitutes in consumption and are unrelated in production. The Ukraine is a major supply source for Product 1. Given the current conflict in Eastern Ukraine, the supply for Product 1 (Market 1) shifts inwards (to the left).
Exercise \(\PageIndex{5}\)
- Which of the following do you know will happen in Market 1?
a) Equilibrium quantity in Market 1 will increase
b) Equilibrium price in Market 1 will decrease
c) Equilibrium price in Market 1 will increase
d) Both a and c
- Answer
-
c
Exercise \(\PageIndex{6}\)
- Which of the following do you know will happen in Market 2?
a) Nothing because the supply shock was in Market 1.
b) Equilibrium price in Market 2 will increase
c) Equilibrium price in Market 2 will decrease
d) Equilibrium quantity in Market 2 will increase
e) Both b and d.
- Answer
-
e
Exercise \(\PageIndex{7}\)
- After considering feedback between these two markets. Which, if any, of the following schedules have not shifted once a new equilibrium is reached?
a) Supply in Market 1
b) Supply in Market 2
c) Demand in Market 1
d) Demand in Market 2
e) All of the above schedules have shifted
- Answer
-
b
Exercise \(\PageIndex{8}\)
- Which best describes the exogenous shock in this situation?
a) The conflict that led to the supply shift to Market 1
b) The change in equilibrium price in Market 1
c) The feedback from Market 2 into Market 1
d) All of the above.
- Answer
-
a
Use the diagram below to answer questions 9 - 12.
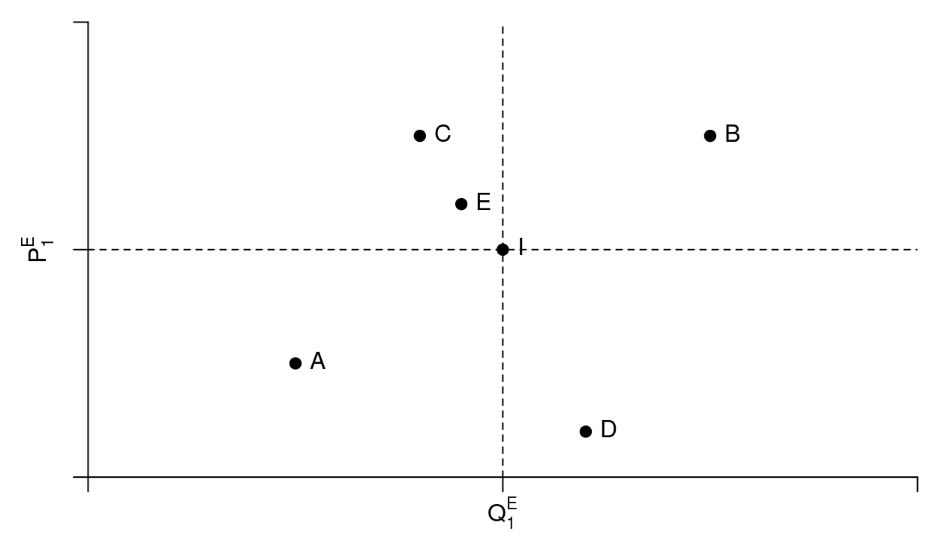
Exercise \(\PageIndex{9}\)
- Point D only
- Points C, D, and E
- Points B and A
- Points C and E
- None of the points
- Answer
-
c
Exercise \(\PageIndex{10}\)
- In which cases do you know for certain that demand has increased relative to the original equilibrium at point I?
a) Point B
b) Points C and E
c) Points B and A
d) Points A
e) None of the points
- Answer
-
a
Exercise \(\PageIndex{11}\)
- In which cases do you know for certain that supply has decreased relative to the original equilibrium at point I?
a) Point B
b) Points C and E
c) Points B and A
d) Points A
e) None of the points
- Answer
-
b
Exercise \(\PageIndex{12}\)
- In which cases do you know for certain that both demand and supply have shifted from the original equilibrium at point I?
a) Point B
b) Points C and E
c) Points B and A
d) Points A
e) None of the points
- Answer
-
e



