6.1: Risk Versus Return
- Last updated
- Save as PDF
- Page ID
- 58462
In finance, a portfolio means the total holdings of stocks, bonds, and other securities of an individual (or other entity, such as a trust or foundation).
Because the investor can decide which securities to include in her portfolio, in other words, because choices are made, we can apply the method of economics. Optimal Portfolio Theory is the name given to the application of the Theory of Consumer Behavior to analyze decisions about which assets to hold.
An important stop on our journey is shown in Figure 6.1, the initial solution to the constrained optimization problem.
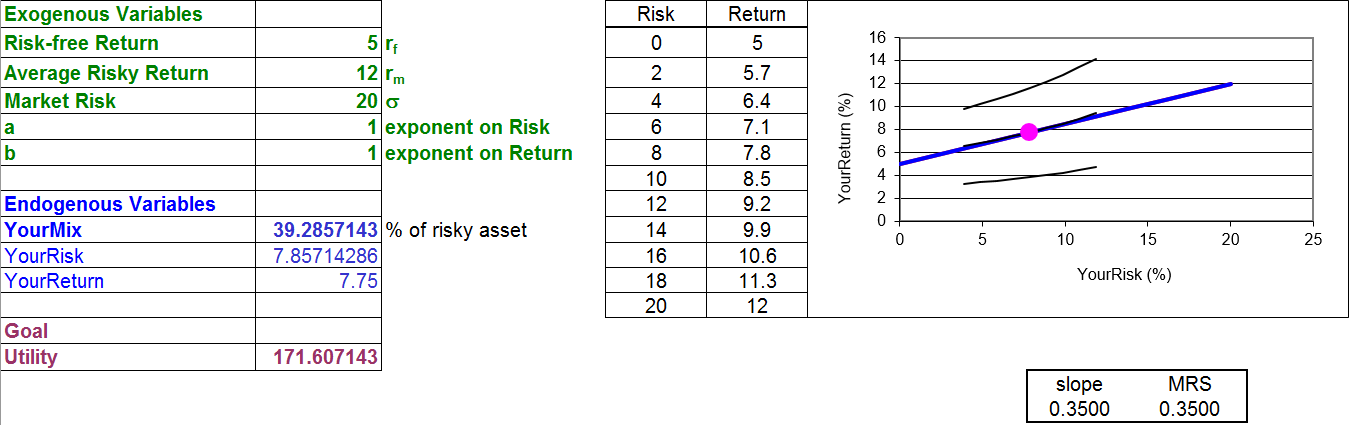
Figure 6.1: The initial solution.
Source: RiskReturn.xls!OptimalChoice
There are some strange features in Figure 6.1 and you are not expected to understand it right away. Perhaps the weirdest thing is that the budget constraint and indifference curves are upward sloping. Because risk (on the x axis) is a bad (not a good), the agent substitutes more of the bad for more of the good (return, on the y axis) on an indifference curve.
There are also, however, elements that are familiar and comfortable in Figure 6.1. There are exogenous (green) and endogenous (blue) variables with a goal. There is a constraint and a few curves with a tangency highlighted that is obviously the optimal solution. And we can see the usual MRS = slope condition below the chart.
Of course, Figure 6.1 is just the initial optimal solution. There is more to do than simply finding the initial solution. That is why Figure 6.1 is an important stop on our journey, but we have more to travel. We want to explore how the optimal solution changes as one of the exogenous variables changes, ceteris paribus. This is called comparative statics analysis.
The procedure that defines the Theory of Consumer Behavior is clear: constraint, preferences, find initial solution, then comparative statics to make statements about how a shock variable affects an optimal choice variable. We will do an elasticity computation and interpretation of the shock. The short way of saying all of this is to just say that we are going to do an economic analysis of portfolio choice.
But since we will be talking about returns from assets, volatility, and the stock market, let’s look at some data to make sure we understand some basic facts.
Stock Market Returns
STEP Open the Excel workbook RiskReturn.xls and read the Intro sheet, then go to the Data sheet.
The sheet has returns from the S&P 500 index, a group of 500 large companies, downloaded from www.moneychimp.com/features/market_cagr.htm.
These data are used to show that returns are quite volatile. The sheet also explains the difference between the arithmetic and geometric mean.
STEP Read the explanation in the Data sheet, scroll down to see the data (all the way down to 1871), and then click the  button.
button.
This reveals more material. Keep reading and clicking the  buttons until you get to the end and then be sure to click the
buttons until you get to the end and then be sure to click the  button.
button.
Of utmost importance is that you understand the volatility in the S&P 500 returns. They swing wildly and unexpectedly, from incredible spurts of 50% to staggering losses of almost negative 50%.
STEP Look in columns A and B of the Data sheet at the 1930s, during the Great Depression. Scroll slowly back up, looking at the data.
The volatility in the stock market, measured by the standard deviation, SD, of almost 20%, is unwelcome and unsatisfying. The fear of financial disaster and the risk of losing money lowers utility.
Then why do people put their money in assets like the S&P 500? Because the overall annual return is highmuch higher than safer, less volatile assets. For the S&P 500, the overall annual return (as you now know, measured by the geometric mean, GM, or compound annual growth rate, CAGR) is about 9% per year.
The stock market’s 9% annual return is much higher than that available from a safe, stable asset that produces consistent annual returns like US Treasury Bills. Cell H10 in the More sheet shows that the SD is a mere three percentage points. The variability arises because the yield changes over time, but once you buy a US Treasury note for a particular length of time, you can be quite sure that you will be paid. But right below the SD we see that the overall annual return is one-third of the stock market’s return.
The key point is that financial markets offer the investor a menu of options, from low risk, low return to high risk, high return, and the investor chooses. All we need to do is model that choice as an optimization problem.
Optimal Portfolio Theory
The Compare, Mix, and Constraint sheets in RiskReturn.xls demonstrate that an investor can mix two assets, a risk-free and a risky asset, to create a portfolio that has a particular combination of risk and return.
The investor is not free to pick any combination of risk and return. They must stay within the constraint imposed by the market. The idea is that you have a fixed amount of money, say $10,000, to allocate across two assets.
The risk-free asset, say a US Treasury Bill, has a certain (practically speaking) rate of return, say 5% per year, which is unrealistically high for the current climate. Thus, you are sure to get 5% of $10,000, or $500, along with your initial investment of $10,000 at the end of the year. Each year, a $10,000 investment is guaranteed to produce $500 of return.
The risky asset, say a mutual fund of stocks, has a greater return, but also volatility in the actual realized return. We will suppose that the actual return will be drawn from a normal distribution centered on 12%, with a spread of 20%. Both of these values are a little higher than the historical experience of the S&P 500 (in the Data sheet). Our parameter values mean that the typical realized value in our hypothetical world will be around 12% \(\pm\) 20% points. It also means you will actually lose money (suffering a negative return) about a quarter of the time.
But this is way too abstract. To understand the meaning of these parameters, let’s work on a concrete problem with actual numbers and a clear display of what is going on.
STEP Go to the Compare sheet.
The bell-shaped curve is the normal distribution from which each year’s return will be drawn. The center and spread are controlled in cells A2 and C2.
The sheet allows you to run the two investments against each other and shows how volatility impacts the annual returns.
STEP Click the  button.
button.
For the risk-free asset, cells I3 and L3 show 5% and $500. In other words, if you place $10,000 in the risk-free asset, these are the returns on that investment.
The risky asset is different. Cells J4 and M4 show a number that is taken from the normal distribution on the left of your screen, centered on 12 with an SD of 20. Thus, the number in J4 is likely to be around 12, but could easily be in the range \(- 8\) to 32 (\(\pm 1\) SD from the average) and roughly 95% of the time will be between \(-28\) and 52 (\(\pm 2\) SDs from 12).
STEP Click the  button a few times.
button a few times.
You can clearly see what is happening here. The return from the risk-free asset is always the same, but the risky asset bounces around.
Once you have more than one year of returns, the display shows more information in columns P:S. You can see the arithmetic mean of the returns, SD, the exact geometric mean, and its approximation.
STEP Click the  button many times, at least 20.
button many times, at least 20.
Notice what is happening to the average of the returns of the risky asset as you keep adding years: The average return is converging to 12% (the average return from the normal distribution in A2). In other words, over the long haul, the risky asset will outperform the risk-free asset. However, in any one year, the risky asset can do pretty badly. Look at your screen to confirm that this is true. You will see some whopper losses (and gains)just like the real-world S&P 500 data.
STEP Click the  button and set the dispersion to 6% (in C2). Repeatedly (many times) click the
button and set the dispersion to 6% (in C2). Repeatedly (many times) click the  button.
button.
The SD of the normal distribution controls the variability. The lower SD makes the normal distribution much more spiked. In other words, the draws from the distribution are much more concentrated at the average and it is much less likely that you will see values far from the center of the distribution.
As you get one yearly return after another (keep drawing more returns), it is easy to see that the returns are much closer to 12%. You will rarely lose money with an average of 12% and an SD of 6%.
In finance, risk is denoted by the Greek letter sigma, \(\sigma\). The SD and \(\sigma\) are the same thing. Both represent risk as volatility and bounce in returns, including the possibility of negative returns. Risk is bad and undesirable. The lower the risk, the better.
What determines the amount of risk in the risky asset? That depends on the asset. We have seen that the S&P 500 has a lot of volatility. From 1871 to 2019, it has experienced an overall annual return of about 9% with an SD of 18%. The More sheet showed that other assets have different volatility. So, the investor is given the average and SD parameters of various assets and chooses what to invest in.
Although we ran risk-free and risky assets in the Compare sheet, in fact, the choice is not simply between a risk-free and a risky asset. You can combine the two in varying proportions.
For example, you could split your investment and put $5000 in the risk-free and $5000 in the risky asset. In this case, your return would be halfway between the risk-free and risky assets: \[\frac{r_f + r_ m}{2} = 8.5\%\] Although the return is lower than using the risky asset alone, your risk, the variability in returns, would be cut in half also.
STEP Proceed to the Mix sheet to see this idea in action.
The Mix sheet is the same as the Compare sheet, except it has a scroll bar in H1 to control the allocation of your $10,000 across the two assets.
STEP After you set the scroll bar value (any value will do; pick the one you think makes the most sense for you), click the  button many times.
button many times.
You should be able to see that the average return for your mix (or portfolio) converges on a return that is in between the risk-free and risky assets. In other words, you can choose the return and risk that you get. You must, however, trade them offmore return requires accepting more risk.
STEP Experiment. Use the  button to try different mixes and parameter values (yellow-backgrounded cells A2, C2, and F2).
button to try different mixes and parameter values (yellow-backgrounded cells A2, C2, and F2).
You can copy the Mix sheet (right-click the sheet tab, select Move or Copy, and check Create a Copy) if you want to compare different scenarios. The more you experiment, the more you learn.
Your work in the Compare and Mix sheets makes understanding the constraint much easier because you have seen that there are two assets that can be mixed to form a portfolio with a continuous range of risk and return possibilities. This constitutes the constraint for the investor. He or she is free to choose combinations of risk and return, trading higher risk for greater return.
STEP Proceed to the Constraint sheet.
There are two endogenous variables, YourRisk and YourReturn, in cells B14 and B15. These are the risk and return you have chosen, in other words, a single point on the budget line. However, we can create a single variable, YourMix (just like in the Mix sheet) that controls the proportion of your investment in the two assets and the values of risk and return you select.
Clearly, you can mix the risk-free and risky assets in any combination from 0 to 100%. Zero means you buy just the risk-free asset and 100% means you buy only the stock market.
Do not confuse the exogenous variable Market Risk with the endogenous variable YourRisk. The riskiness of the risky asset, sigma, is exogenous to the agent. But the agent determines how much risk to take and, therefore, the chosen amount of risk is endogenous.
STEP Change B13 to 20%, 50%, and 90%.
As you change B13, the red dot moves on the constraint. You can put the red dot wherever you like along the line. At 50%, you are setting YourRisk to 10% (this is the variability in the 50/50 portfolio) and YourReturn to 8.5% (halfway between \(r_f\) and \(r_m\)).
The equation of the budget line (derived in the Constraint sheet) is \[YourReturn = r_f + \frac{r_m - r_ f}{\sigma}YourRisk\] Clearly, if you choose a risk of zero, then your return is the risk-free return. This is the y intercept. As you accept more risk, your return grows with a slope given by \(\frac{r_m - r_ f}{\sigma}\)
Notice that combinations under the budget constraint are feasible, but will not be selected because more return can always be obtained at the same risk by going straight up. Points to the northwest of the line are more desirable, but are unattainable.
Which mix is the best, the optimal choice? We cannot answer this question with the constraint alone. It tells us only the choices we can make. To answer the question, we need to model preferences.
But before we leave the constraint, let’s explore the effect of a change in sigma, Market Risk. This will be our shock variable when we do comparative statics analysis.
Remember when you lowered the SD to 6% and that made the variability in the risky asset go way down? That was a welcome shock. What would happen to the constraint if we applied that shock? Before we do it, ponder the question. Do you have an answer? Let’s see how you did.
STEP Change Market Risk, cell B10, to 6.
The budget line rotates up (counterclockwise) around the y intercept. This gives the investor access to higher returns with the same risk or the same return with less risk. Mathematically, it also makes sense since we lowered the denominator in the slope, so the slope term increased, making the line steeper.
STEP Proceed to the Preferences sheet to see how we handle risk as a bad.
Our usual Cobb-Douglas functional form can be modified to reflect a bad with a simple tweak: \[U(YourRisk,YourReturn)=(30-YourRisk)^aYourReturn^b\] The clever trick here is subtracting a variable from a constant, which has been chosen to be bigger than the possible values of the variable. By having a constant, 30, which is a bigger number than the relevant range for Risk (from zero to 20), as we increase the chosen amount of YourRisk, \(30 – YourRisk\) falls. This gives us a bad because utility falls as YourRisk rises (for \(YourRisk < 30\)). YourReturn is a goodas YourReturn rises, so does utility.
The chart shows three representative, upward sloping indifference curves. The investor gets equal satisfaction by the combinations of risk and return on a single indifference curve. If the investor takes on more risk, she must be given more return to compensate.
STEP The agent is free to choose any combination of risk and return that is on the budget line. Change B12 to 50.
Figure 6.2 shows the result. In addition to the three original indifference curves with a black dot, three new curves are displayed along with a red dot. The black dot is the initial 75% mix choice and it produced Dead Utility of 153.75 and a Dead MRS of about 0.6833.
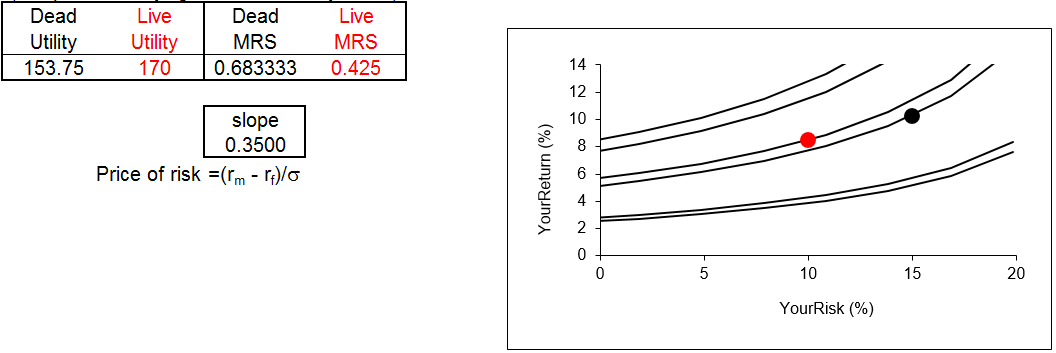
Figure 6.2: The investor’s indifference map, \(a=b=1\).
Source: RiskReturn.xls!Preferences
The red dot is live in the sense that it depends on the value of B10. The chart displays the indifference curve that goes through the mix value in B10, along with an indifference curve and another below it.
A mix of 50% risky is better than 75% for this investor because utility went up. The red dot is on a higher indifference curve. Notice also that the MRS fell, getting closer to the slope of the budget line. That means the investor is getting closer to the optimal solution.
STEP Change B12 to 90.
Now the reverse is true. The red dot is on a lower indifference curve and the MRS is farther away from the slope.
STEP Change the exponent on YourReturn in B19 to 4 and click the button.
The indifference curves are now much flatter. What does this mean?
STEP Change B12 to 50 and 90.
We are getting different results than before? What is going on?
If \(b > a\), the investor cares more about return than risk. The flat indifference curves (with low MRS) mean that they are willing to accept a lot of risk for a little more return. These preferences mean that this investor will find an optimal solution with a high risk, high return combination.
STEP Change B19 to 0.4 and click the  button. Explore the satisfaction produced by mixes of 50% and 90%. What do you learn?
button. Explore the satisfaction produced by mixes of 50% and 90%. What do you learn?
With a low b (lower than a), this investor is more concerned with risk. They are conservative and their optimal solution will lie on a low mix value. In fact, these preferences produce a corner solution, with the investor putting all $10,000 into the risk-free asset.
Preferences are not right or wrong. If you are young and saving for retirement, it makes sense that \(a < b\), but even then, if a person does not like risk, that is not a defect. An aggressive investor is not in any sense better than a conservative investor. Some people like risk and others do not in the same way that some people like broccoli or the color blue and others do not.
Preferences are not set in stone. They can be affected by the environment. A short time horizon, such as needing funds for college in a year, will rotate the indifference map, reflecting an investor who is more conservative. Likewise, retired people, typically, become more conservative and less willing to accept risk.
With the constraint and preferences modeled, we are ready to find the optimal solution.
STEP Proceed to the OptimalChoice sheet to see the numerical method in action.
The OptimalChoice sheet opens with an inefficient solution. The MRS is greater than the slope of the budget line so the indifference curve cuts the line. The agent should move down the line, accepting less return for less risk. This increases satisfaction. But how far down to travel?
STEP Run Solver to find the answer to this question.
At the optimal solution, the MRS equals the slope of the budget line and the agent is on the highest attainable indifference curve.
For this agent (with these attitudes toward risk and return) and the given market trade-off between risk and return (captured by the equation of the budget constraint), the optimal solution is found with a mix of about 39% of funds invested in the risky asset. Thus, the optimal risk to accept is \(7 \frac{6}{7}\) and the optimal return is \(7 \frac{3}{4}\).
Via analytical methods, we can use this Lagrangean to find optimal YourRisk (\(x_1\)) and YourReturn (\(x_2\)).
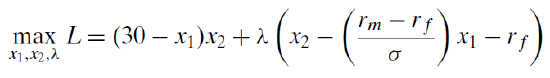
Try doing this problem and if you get stuck, the solution for a similar problem in the Q&A sheet is in the Answers folder.
Comparative Statics
As usual, there are a number of comparative statics exercises to consider and they can be done via numerical or analytical methods. Let’s explore the effect of an increase in sigma, the amount of risk the market forces you to bear in return for better performance.
STEP In the OptimalChoice sheet, increase \(\sigma\) from 20 to 25. What happens?
Figure 6.3 and your screen show a new, red budget line that has rotated clockwise and down.
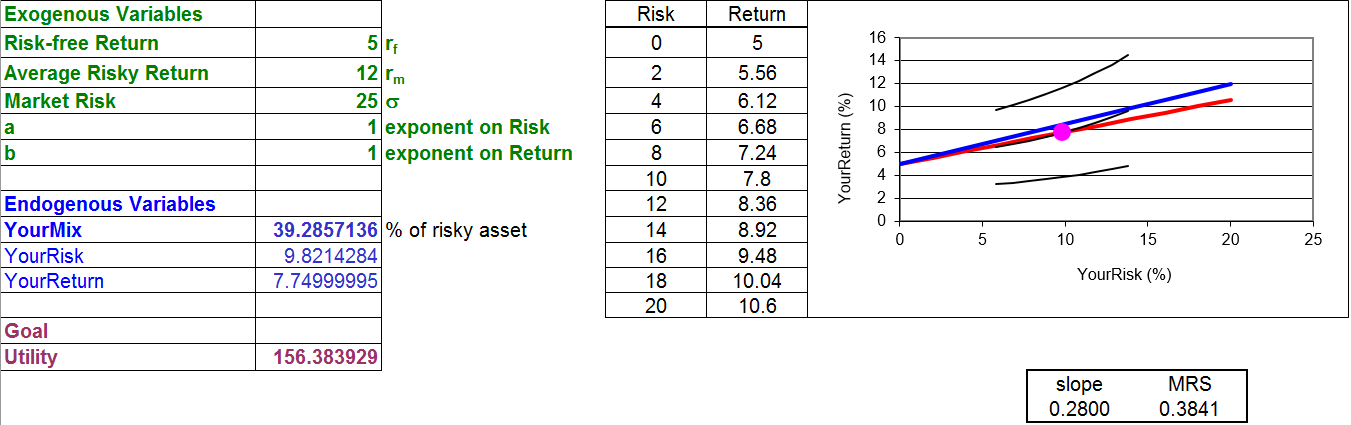
Figure 6.3: Increasing sigma, Solver yet to be run.
Source: RiskReturn.xls!OptimalChoice
The flatter slope is bad for the investor because consumption possibilities have been reduced. The market says that for a given amount of return, you must accept more risk. How will the investor respond to this shock?
STEP Run Solver to find out.
You will see that the agent chooses less risk and less return. What elasticity is under consideration here? There are several. There is the sigma elasticity of YourRisk, the sigma elasticity of YourReturn, and the sigma elasticity of YourMix.
Of course, these elasticities can also be computed at a point, using the derivative. One of the exercises asks you to do exactly that.
STEP Try your hand at computing the sigma elasticity of YourRisk from \(\sigma = 20\%\) to 25%. Check your answer in the CSsigma sheet.
Of course, these elasticities can also be computed at a point, using the derivative. One of the exercises asks you to do exactly that.
Because the change in sigma is a change in the slope of the budget line, we can use the Slutsky decomposition approach to break down the total effect into income and substitution effects. This work is left for you as an exercise.
Asset Allocation is an Optimization Problem
Optimal Portfolio Theory is yet another application of the Theory of Consumer Behavior. The twist here is that one of the choices, risk, is a bad. The agent cannot ignore risk. She is forced to accept more risk to secure greater return.
The core concepts of the Theory of Consumer Behavior remain easily visible: a budget constraint describing consumption possibilities, preferences translated into an indifference map, maximization of utility given a budget constraint, and MRS equals slope of budget line at the optimal solution.
Perhaps most importantly, once we cast the problem as a choice, how to allocate assets among stocks, bonds, and other financial instruments, we are firmly in the land of Economics. This particular optimization problem is different from previous applications in that individuals are keenly interested in getting the optimal solution right. There is often a lot of money at stake and mistakes can prove costly (for example, with a retirement portfolio).
As economists, we remain interested in comparative statics. Changing preferences are an important shock variable in this application. We do not shake our heads at the conservative investor who finds an optimal solution (given conservative preferences) at a low risk, low return point.
Exercises
- Use the equation that follows to solve for YourRisk* (\(x_1\)) and YourReturn* (\(x_2\)) in terms of the exogenous variables. Show your work.
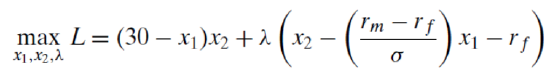
- Use your reduced form solution to find the sigma elasticity of YourRisk at \(\sigma = 20\%\) (and the values of the other exogenous variables from the initial position of the OptimalChoice sheet-click the
 button if needed). Show your work.
button if needed). Show your work.
- Use Word’s Drawing Tools to draw a well-labeled graph that depicts the total, income, and substitution effects for YourRisk. Make the substitution effect greater than an opposing income effect.
- Compute the total, income, and substitution effects for YourRisk for the change in sigma from 20% to 25%. Show your work and describe your procedure.
References
The epigraph is from page 184 (9th edition) of a classic, excellent book on personal finance and the stock market. A Random Walk Down Wall Street by Burton Malkiel was originally published in 1973 by W. W. Norton & Company and the 12th edition came out in 2020. This is not one of those silly books with a scheme to beat the market. Malkiel is sober and reliable. On page 26, he says,
Let me make it quite clear that this is not a book for speculators; I am not going to promise you overnight riches. I am not promising you stock-market miracles. Indeed, a subtitle for this book might well have been The Get Rich Slowly but Surely Book.
For a much deeper analysis of finance with an Excel-based presentation style, see Principles of Finance with Excel by Simon Benninga (New York: Oxford University Press, 2017. 3rd edition).


