3.8: Individual and market functions
- Page ID
- 45740
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
Figure 3.9 Summing individual demands

At P1 individual A purchases  and B purchases
and B purchases  . The total demand is the sum of these individual demands at this price (Q1). At P2 individual demands are summed to Q2. Since the points Q1 and Q2 define the demands of the market participants it follows that market demand is the horizontal sum of these curves.
. The total demand is the sum of these individual demands at this price (Q1). At P2 individual demands are summed to Q2. Since the points Q1 and Q2 define the demands of the market participants it follows that market demand is the horizontal sum of these curves.
 and B purchases
and B purchases  . The total demand is the sum of these individual demands at this price (Q1). At P2 individual demands are summed to Q2. Since the points Q1 and Q2 define the demands of the market participants it follows that market demand is the horizontal sum of these curves.
. The total demand is the sum of these individual demands at this price (Q1). At P2 individual demands are summed to Q2. Since the points Q1 and Q2 define the demands of the market participants it follows that market demand is the horizontal sum of these curves.


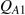 and
and 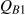 respectively. Thus
respectively. Thus 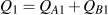 . At a price P2, they purchase
. At a price P2, they purchase 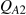 and
and 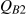 . Thus
. Thus 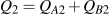 . The
. The 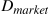 .
.