6.4: The multiplier - Changes in aggregate expenditure and equilibrium output
- Page ID
- 45766
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)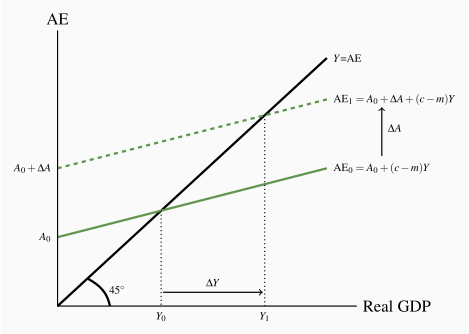
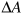 shifts AE up to
shifts AE up to 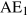 . Equilibrium GDP rises by a larger amount from Y0 to Y1.
. Equilibrium GDP rises by a larger amount from Y0 to Y1.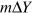 ). Firms increase output again to meet this increased demand, further increasing household incomes. Consumption and imports rise further. This is a first and important example of interdependency and feedback in a basic model. A change in autonomous expenditure, either positive or negative, changes income which in turn causes a change in induced expenditure. Equilibrium income changes by the change in autonomous expenditure plus the change in induced expenditure.
). Firms increase output again to meet this increased demand, further increasing household incomes. Consumption and imports rise further. This is a first and important example of interdependency and feedback in a basic model. A change in autonomous expenditure, either positive or negative, changes income which in turn causes a change in induced expenditure. Equilibrium income changes by the change in autonomous expenditure plus the change in induced expenditure.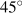 line. Households increase their expenditure when incomes rise, but they increase expenditure by less than the rise in income. Equilibrium moves from Y0 to Y1. Equilibrium output rises more than the original rise in investment,
line. Households increase their expenditure when incomes rise, but they increase expenditure by less than the rise in income. Equilibrium moves from Y0 to Y1. Equilibrium output rises more than the original rise in investment, 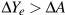 , but does not rise without limit.
, but does not rise without limit.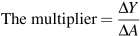 |
(6.3) |
| Initial | New | Initial | New | ||
| GDP | Autonomous | Autonomous | Induced | Aggregate | Aggregate |
| (Y) | Expenditure | Expenditure | Expenditure | Expenditure | Expenditure |
| (A0=100) | (A1=125) | (c–m)Y=0.5Y | 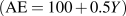 |
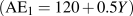 |
|
| (1) | (2) | (3) | (4) | (5) | (6) |
| 175 | 100 | - | 87.5 | 187.5 | 187.5 |
| 200 | 100 | - | 100 | 200 | 200 |
| 225 | 125 | 112.5 | 237.5 | ||
| 237.5 | 125 | 118.75 | 243.5 | ||
| 243.5 | 125 | 121.75 | 246.75 | ||
| 246.75 | 125 | ||||
| – | 125 | ||||
| 250 | 125 | 125 | 250 | ||
| 300 | 125 | 150 | 275 |
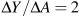 .
. line to show equilibrium Ye=200. Example Box 6.2 at the end of the chapter illustrates the multiplier effect of a change in autonomous expenditure on equilibrium income using simple algebra.
line to show equilibrium Ye=200. Example Box 6.2 at the end of the chapter illustrates the multiplier effect of a change in autonomous expenditure on equilibrium income using simple algebra.The size of the multiplier
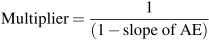 |
(6.4) |
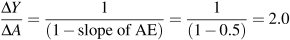
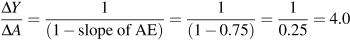



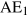 . Before we go into detail, think about what is likely to happen to output. It will rise, but by how much?
. Before we go into detail, think about what is likely to happen to output. It will rise, but by how much?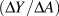 : the ratio of the change in equilibrium income Y to the change in autonomous expenditure A that caused it.
: the ratio of the change in equilibrium income Y to the change in autonomous expenditure A that caused it.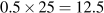 . However GDP(Y) is only 225 and planned expenditure is accommodated by a decrease in inventories of 12.5. This unintended fall in inventories is an incentive to increase production to take advantage of higher than expected sales. The incentive exists until producers increase output and income to 250. Aggregate expenditure rises as income increases until equilibrium is reached at Y=250. At that point actual inventory investment meets producer plans.
. However GDP(Y) is only 225 and planned expenditure is accommodated by a decrease in inventories of 12.5. This unintended fall in inventories is an incentive to increase production to take advantage of higher than expected sales. The incentive exists until producers increase output and income to 250. Aggregate expenditure rises as income increases until equilibrium is reached at Y=250. At that point actual inventory investment meets producer plans.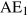 . Now a change in autonomous expenditure raises income and causes a higher change in induced expenditure. As a result the multiplier for this economy would be:
. Now a change in autonomous expenditure raises income and causes a higher change in induced expenditure. As a result the multiplier for this economy would be: