Basic economic growth theory steps back from short-run variations in growth rates. It applies to the very long run, a time frame in which wages and prices are fully flexible, and the labour force, the stock of capital equipment, and the technology used in production can change. In this time frame, output fluctuations around potential output are swamped by the growth of potential output itself.
Very long run: the time required for changes to occur in the stock of capital, the size of the labour force, and the technology of production.
The aggregate production function used in Section 11.2 described the links between inputs to production and real GDP produced. Recall that, for the whole economy, Y is real GDP produced by using inputs of labour (N) and capital (K). The function F tells us how much we get out of particular amounts of labour and capital used in the production process.
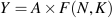 |
(13.1) |
The function F(...) does not change, but changes in N and K cause changes in output Y. Technical progress or improvements in technology are captured separately through A, which measures the state of technology at any date. As technology improves, A increases and more real GDP is produced from the same inputs of labour and capital. A 10 percent increase in A gives 10 percent more real GDP from the same inputs of labour and capital. We describe this as an increase in productivity because outputs per worker and per unit of capital increase. A is often called a measure of total factor productivity (TFP).
Total factor productivity (TFP): output relative to the combined inputs of labour and capital, the total factor inputs to production.
Actual real GDP is the output produced at any time based on the actual inputs of capital and labour. In terms of the production function:
- Yt is real GDP in year t;
- At is determined by the current state of technology; and
- Kt and Nt measure the actual use of capital and labour.
These inputs are combined to give output in year t:
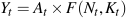 |
(13.2) |
Potential output is the real GDP produced when labour and capital are employed at equilibrium rates using the best available technology. A specific production function to recognize this is:
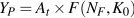 |
(13.3) |
YP is potential output produced by operating plants and machinery at their designed capacity (K0) and using the full employment equilibrium supply of labour services (NF). At is the state of knowledge and technology used in the production process and reflected in the productivity of labour and capital.
Any growth in the potential output of goods and services then comes from growth in labour inputs to production, growth in capital inputs to production, and changes in factor productivity as a result of new and improved technology.
Growth accounting measures the sources of growth in real GDP. From the production function, it follows that:
| |
|
Effect of |
|
Effect of |
|
Effect of |
| Growth in |
= |
Growth in |
+ |
Growth |
+ |
Growth in |
| Real GDP |
|
Total Factor |
|
in Labour |
|
Capital |
| |
|
Productivity |
|
Inputs |
|
Inputs |
Growth accounting: measurement of the contributions of labour, capital, and technology to growth in output.
The way that growth in capital and labour affects the growth in total output can be measured by the incomes they receive. The income approach to the measurement of net domestic product and GDP identifies these factor income shares in Canada in 2013 as the sum of:
| Employee compensation |
$957 billion |
| Net Corporate surplus |
$240 billion |
| Net mixed income |
$168 billion |
| Total factor income |
$1,365 billion |
From that data, employment income was about 70 percent of factor income. This is higher than the longer-term average share of employment income in total factor income, but it shows where the measure comes from. Labour's average contribution to and share of national income, measured over time periods of many years, is approximately two-thirds of total factor income. Capital's contribution and share is the remaining one-third of factor income.
The growth in potential GDP over time can then be expressed as the growth in total factor productivity plus the weighted sum of the growth in the capital and labour inputs to production as follows:

This is the basic growth accounting equation.
The weights (2/3) and (1/3) applied to growth in labour and capital inputs are based on their shares in national income. They determine the rate of growth in real GDP as a result of growth in the inputs of capital and labour. By these weights, a 10 percent increase in labour input, capital and technology held constant, would result in an increase in real GDP of 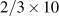 percent, which is 6.6 percent. Similarly, a 10 percent increase in capital input would result in a
percent, which is 6.6 percent. Similarly, a 10 percent increase in capital input would result in a 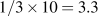 percent increase in real GDP. However, if both N and K grow by 10 percent real GDP grows by 10 percent.
percent increase in real GDP. However, if both N and K grow by 10 percent real GDP grows by 10 percent.
The increase in productivity from improvements in technology cannot be seen and measured directly. As a result, growth accounting classifies these effects as a residual. The difference between the growth in real GDP and the weighted sum of the growth in labour and capital inputs is called the Solow residual, named after Professor Robert Solow, whose work on growth theory was recognized with a Nobel Prize. The Solow Residual is a measure of the contribution to growth made by improvements in the technology of production that raise the productivity of both labour and capital.
Solow residual: the growth in real GDP or per capita real GDP not caused by growth in factor inputs, but attributed to improved technology.
The Solow residual measured by growth in A is found by rearranging the growth accounting equation as follows:

The numerical example in Table 13.3 illustrates the procedure. It assumes data are available for a specific sample period; say 10 years, for the growth rates of real GDP, capital stock, and employment, measured as average annual percentage changes.
Table 13.3 An estimate of the Solow residual using growth accounting
Observed average annual growth rates,  , in: , in: |
| |
Real GDP(Y) 5.0 |
Employment(N) 2.4 |
Capital stock(K) 3.9 |
| By growth accounting: |
| |
Growth in A=5.0–(2/3)(2.4)–(1/3)(3.9) |
| |
Growth in A=5.0–1.6–1.3 |
| |
Contribution of growth in A to growth in real GDP=2.1 percent |
The calculation made using growth accounting shows that the increased productivity of both labour and capital resulting from improvements in technology was the source of 2.1 percent of the 5.0 percent growth in real GDP in this example.
Recent research at the Bank of Canada estimated the sources of growth in real GDP and potential GDP in Canada over the period 1950 to 1996 and projections for future growth in potential GDP. The contributions of capital and labour inputs are weighted as in the simple example above. Growth in actual and potential real GDP are the result of growth in factor inputs and the growth in productivity coming from improvements in the technology of production.
That work shows growth in real GDP and potential GDP declined over the 1950 to 1996 period. This slowdown was partly a result of a slowdown in the growth of population, and labour and capital inputs to production. But starting in the 1970s there was also a slowdown in productivity growth, which reduced the rate of growth of output per worker. This slowdown in productivity is examined in more detail later in this chapter. It had important implications for the standard of living in many countries, including Canada. Some further research on productivity growth in Canada by the Centre for the Study of Standards of Living, www.csls.ca, and at the Bank of Canada has uncovered another productivity slowdown in Canada relative to the United States after the year 2000, which has continued and is a current source of concern.
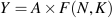
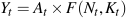
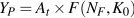


 , in:
, in:


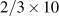 percent, which is 6.6 percent. Similarly, a 10 percent increase in capital input would result in a
percent, which is 6.6 percent. Similarly, a 10 percent increase in capital input would result in a 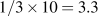 percent increase in real GDP. However, if both N and K grow by 10 percent real GDP grows by 10 percent.
percent increase in real GDP. However, if both N and K grow by 10 percent real GDP grows by 10 percent.