6.6: Exercises for Chapter 6

EXERCISE 6.1

In the example given in Table 6.1, suppose Neal experiences a small increase in income. Will he allocate it to snowboarding or jazz? [Hint: At the existing equilibrium, which activity will yield the higher MU for an additional dollar spent on it?]

EXERCISE 6.2

Suppose that utility depends on the square root of the amount of good X consumed: .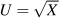

1. In a spreadsheet enter the values 1... 16 as the X column (col A), and in the adjoining column (B) compute the value of utility corresponding to each quantity of X. To do this use the 'SQRT' command. For example, the entry in cell B3 will be of the form '=SQRT(A3)'.

2. In the third column enter the marginal utility (MU) associated with each value of X – the change in utility in going from one value of X to the next.

3. Use the 'graph' tool to map the relationship between U and X.

4. Use the graph tool to map the relationship between MU and X.

EXERCISE 6.3

Instead of the square-root utility function in Exercise 6.2, suppose that utility takes the form U=x².

1. Follow the same procedure as in the previous question – graph the utility function.

2. Why is this utility function not consistent with our beliefs on utility?

EXERCISE 6.4

1. Plot the utility function U=2X, following the same procedure as in the previous questions.

2. Next plot the marginal utility values in a graph. What do we notice about the behaviour of the MU?

EXERCISE 6.5

Let us see if we can draw a utility function for beer. In this instance the individual may reach a point where he takes too much.

1. If the utility function is of the form U=6X–X², plot the utility values for X values in the range , using either a spreadsheet or manual calculations.

2. At how many units of X (beer) is the individual's utility maximized?

3. At how many beers does the utility become negative?

EXERCISE 6.6

Cappuccinos, C, cost $3 each, and music downloads of your favourite artist, M, cost $1 each from your iTunes store. Income is $24.

1. Draw the budget line, with cappuccinos on the vertical axis, and music on the horizontal axis, and compute the values of the intercepts.

2. What is the slope of the budget constraint, and what is the opportunity cost of 1 cappuccino?

3. Are the following combinations of goods in the affordable set: (4C and 9M), (6C and 2M), (3C and 15M)?

4. Which combination(s) above lie inside the affordable set, and which lie on the boundary?

EXERCISE 6.7

George spends his income on gasoline and "other goods."

1. First, draw a budget constraint, with gasoline on the horizontal axis.

2. Suppose now that, in response to a gasoline shortage in the economy, the government imposes a ration on each individual that limits the purchase of gasoline to an amount less than the gasoline intercept of the budget constraint. Draw the new effective budget constraint.

EXERCISE 6.8

Suppose that you are told that the indifference curves defining the trade-off for two goods took the form of straight lines. Which of the four properties outlines in Section 6.3 would such indifference curves violate?

EXERCISE 6.9

Draw an indifference map with several indifference curves and several budget constraints corresponding to different possible levels of income. Note that these budget constraints should all be parallel because only income changes, not prices. Now find some optimizing (tangency) points. Join all of these points. You have just constructed what is called an income-consumption curve. Can you understand why it is called an income-consumption curve?

EXERCISE 6.10

Draw an indifference map again, in conjunction with a set of budget constraints. This time the budget constraints should each have a different price of good X and the same price for good Y.

1. Draw in the resulting equilibria or tangencies and join up all of these points. You have just constructed a price-consumption curve for good X. Can you understand why the curve is so called?

2. Now repeat part (a), but keep the price of X constant and permit the price of Y to vary. The resulting set of equilibrium points will form a price consumption curve for good Y.

EXERCISE 6.11

Suppose that movies are a normal good, but public transport is inferior. Draw an indifference map with a budget constraint and initial equilibrium. Now let income increase and draw a plausible new equilibrium, noting that one of the goods is inferior.

1. Note that, with two snowboard outings and seven jazz club visits, total utility is 352 (=132+220), while the optimal combination of four of each yields a total utility of 380 (=224+156).