1.4: Welfare Economics - Consumer and Producer Surplus
- Last updated
- Save as PDF
- Page ID
- 43148
Introduction to Elasticities
An elasticity is a measure of responsiveness.
Elasticity = How responsive one variable is to a change in another variable.
An elasticity \((E)\), or responsiveness, is measured by the percentage change of each variable. The change in a variable is the ending value \((X_1)\) minus the initial value \((X_0)\), or \(ΔX = X_1 – X_0\). A percentage change in a variable is defined as the change in the variable divided by the initial value of the variable:
\[\%ΔX = \dfrac{ΔX}{X_0}.\]
Using this formula, Equation \ref{1.7} shows the responsiveness of \(Y\) to a change in \(X\):
\[E = \frac{\%ΔY}{\%ΔX} = \frac{(ΔY/Y)}{(ΔX/X)} = \left(\frac{ΔY}{ΔX}\right)\left(\frac{X}{Y}\right). \label{1.7}\]
Elasticities can be calculated for any two variables. Elasticities are widely used in economics to measure how responsive producers and consumers are to changes in prices, income, and other economic variables. Elasticities have a very desirable property: they do not have units. Since the two variables are measured in percentage changes, the units of each variable are cancelled, and the resulting elasticity has no units. This allows elasticities to be compared to each other, when prices and quantities cannot be directly compared. For example, the quantity of apples cannot be directly compared to the quantity of orange juice, since they are in different units. However, the elasticities of oranges and apples can be compared directly, since there are no units for elasticities.
Own Price Elasticity of Demand: Ed
The own-price elasticity of demand (most often called simply the “price elasticity of demand” or the “elasticity of demand”) measures the responsiveness of consumers to a change in price, as shown in Equation \ref{1.8}:
\[E_d = \frac{\%ΔQ^d}{\%ΔP} = \left(\frac{ΔQ^d}{ΔP}\right)\left(\frac{P}{Q^d}\right).\label{1.8}\]
Own Price Elasticity of Demand = the percentage change in quantity demanded given a one percent change in the good’s own price, ceteris paribus.
The own-price elasticity of demand is the most important thing that a business firm can know. The price elasticity informs the business about how a change in price will affect the quantity demanded. If consumers are responsive to price changes, the firm may think twice before raising the price and losing customers to the competition. On the other hand, if consumers are relatively unresponsive to price changes, the firm may increase the price, and most customers will continue to purchase the good at the higher price. Food is an example of an inelastic good, since we all need to eat.
The price elasticity of demand \((E_d)\) depends on the availability of substitutes. If there are no substitutes for a good (food, toilet paper, toothpaste), the good is called, “price inelastic.” Consumers will purchase the good even at a high price. If substitutes are available, the good is considered to be “price elastic:” a higher price will cause customers to decrease consumption of the good by buying the substitute good. Green shirts are an example: if the price of green shirts is increased, consumers will shift purchases to blue shirts, or shirts of a different color.
The price elasticity of demand is the most critical aspect of a business firm, since it provides the most crucial information about customers! Knowledge of the price elasticity of demand provides information to a business firm on how consumers would react to price changes, allowing the firm to identify the profit-maximizing price to charge consumers.
Price Elasticity of Demand Example
Suppose that the price of wheat is equal to USD 4/bu of wheat, and increases to USD 6/bu. Due to the higher price, suppose that wheat millers reduce their purchases of wheat from 10 million bushels (m bu) to 8 million bushels. The price elasticity of demand for wheat can be calculated using Equation \ref{1.9}. By convention, the initial values of \(P\) and \(Q^d\) are used in the elasticity calculation for the variables \(P\) and \(Q^d\).
\[E_d = \frac{\%ΔQ^d}{\%ΔP} = \frac{(ΔQ^d/ΔP)}{(P/Q^d)} = \left(\frac{\text{8-10 m bu}}{\text{6-4 USD/mt}}\right)\cdot\left(\frac{\text{4 USD/bu}}{\text{10 m bu}}\right)\label{1.9}\]
Notice that the units cancel: there are (m bu) in both the numerator and denominator, and (USD/bu) also appears in both numerator and denominator. This allows the math to be greatly simplified:
\[E_d = \left(\frac{-2}{2}\right)\cdot\left(\frac{4}{10}\right) = \frac{-1}{0.4} = -0.4\]
The price elasticity of demand is always negative, due to the Law of Demand. By convention, economists take the absolute value to make \(E_d\) positive. For example, in this case, \(E_d= – 0.4\), then \(\mid E_d \mid = 0.4\). The own price elasticity of demand provides important information about the wheat market: how responsive wheat buyers are to a change in price. To interpret the elasticity, it means that for a one percent increase in price, the quantity demanded of wheat will decrease by 0.4 percent. This is a relatively inelastic response, since the change in quantity demanded is smaller than the price change.
Elasticities are classified into three categories, based on consumer responsiveness to a one percent change in price.
\[\begin{align*} &\text{Price elastic } & \mid E_d \mid &> 1\\ &\text{Price inelastic} & \mid E_d \mid &< 1\\ &\text{Unitary elastic} & \mid E_d \mid &= 1\end{align*}\]
Goods that are price elastic have substitutes available, and the percentage change in quantity demanded will decrease more than the percentage increase change in price \((\%ΔQ^d > \%ΔP\), therefore \(\mid E_d\mid > 1)\). A price inelastic good, on the other hand, will have a smaller percentage change in quantity demanded than the percentage increase in price \((\%ΔQ^d < \%ΔP\), therefore \(\mid E_d \mid < 1)\). For unitary elastic goods, the percentage change in quantity demanded is equal to the percentage change in price \((\%ΔQ^d = \%ΔP\), therefore \(\mid E_d\mid = 1)\).
Elastic and Inelastic Demand Examples
To compare elastic and inelastic demands, think of a student who would like to purchase a pack of cigarettes during a late night study session for an exam. If the student arrives at the convenience store to find that the price of Marlboros, her usual brand, has doubled, she could switch to many other brands: Lucky Strikes, Winstons, etc. The demand for Marlboro cigarettes is price elastic (left panel, Figure \(\PageIndex{1}\)). The price elasticity of demand depends on the availability of substitutes. An elastic demand will have a relatively flat slope, since a small change in price results in a relatively larger change in quantity demanded.
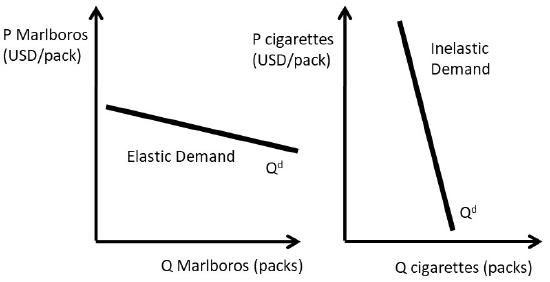
On the other hand, if the convenience store increases the price of all cigarettes, the student will pay for a pack, since there are no substitutes for all cigarettes (right panel, Figure \(\PageIndex{1}\)). More narrowly defined goods will have larger absolute values of own price elasticities, since there are more substitutes for narrowly defined goods. For example, apples are more price elastic than all fruit, and green shirts are more price elastic than all shirts. An inelastic good will have a steep slope, since the change in quantity demanded is small relative to the change in price.
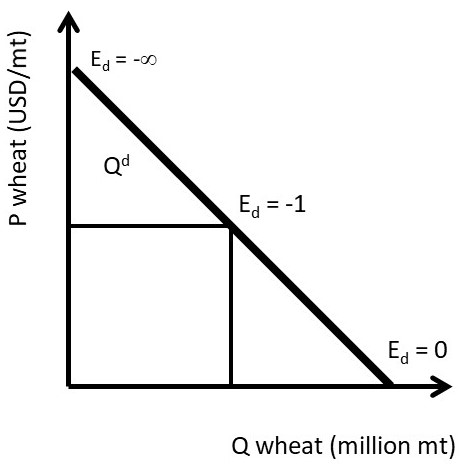
Figure \(\PageIndex{2}\) shows a range of own price elasticities, from perfectly inelastic to perfectly elastic.
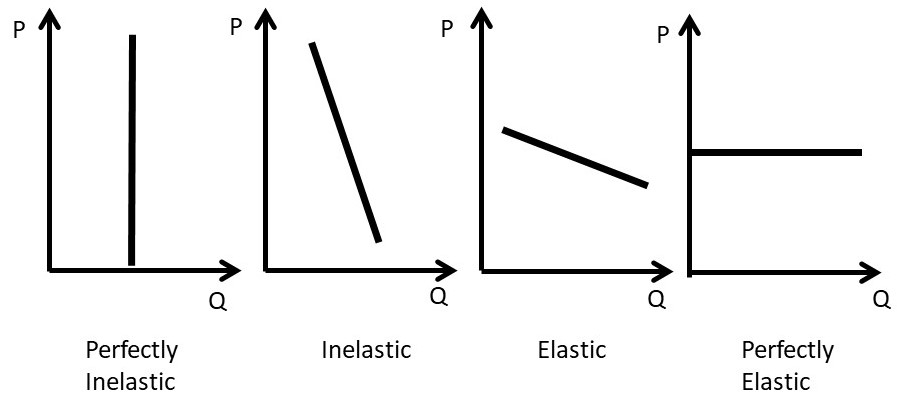
A good that is perfectly inelastic is one that consumers purchase no matter what the price is. Within a certain range of prices, this could be food or electricity. In this case, quantity demanded is completely unresponsive to changes in price: \(\mid E_d\mid = 0\). An inelastic demand is one where the percentage change in price is larger than the percentage change in quantity demanded: \(\%ΔQ^d < \%ΔP\), and \(\mid E_d\mid < 1\). Goods that are price inelastic are characterized by consumers being unresponsive to price changes. Goods that are price elastic exhibit relatively high levels of consumer responsiveness to price movements. For elastic goods, the percentage change in quantity demanded is larger than the percentage change in price: \(\%ΔQ^d > \%ΔP\), and \(\mid E_d\mid > 1\). A perfectly elastic good is characterized by a horizontal demand curve. In this case, if the price of the good is increased even one cent, all customers decrease purchases of the good to zero. An individual wheat farmer’s crop is an example. If the farmer tries to raise the price by one cent more than the prevailing market price, no consumers would purchase her wheat. There are a large number of perfect substitutes available from other wheat farmers, so the price elasticity is infinite, and the good is called, “perfectly elastic.”
Own Price Elasticity of Supply: Es
Producer responsiveness to a change in price is measured with the own price elasticity of supply, often called the price elasticity of supply, or the elasticity of supply (Es). The formula for the price elasticity of supply is given in Equation \ref{1.10}:
\[E_s = \frac{\%ΔQ^s}{\%ΔP}. \label{1.10}\]
Own Price Elasticity of Supply = the percentage change in quantity supplied given a one percent change in the good’s own price, ceteris paribus.
The own price elasticity of supply is always positive, because of the Law of Supply: there is a direct, positive relationship between the quantity supplied of a good and the good’s own price, ceteris paribus. Similar to the price elasticity of demand, the price elasticity of supply is categorized into three elasticity classifications.
\[\begin{align*} &\text{Price elastic } & E_s &> 1\\ &\text{Price inelastic} & E_s &< 1\\ &\text{Unitary elastic} & E_s &= 1\end{align*}\]
A good with an elastic supply is one where the percentage change in quantity supplied is greater than the percentage change in price: \(\%ΔQ^s > \%ΔP\), and \(E_s > 1\). Since \(E_s\) is always positive, the absolute value is not necessary (redundant). A good with an inelastic supply has a smaller percentage change in quantity supplied, given a percent change in price: \(\%ΔQ^s < %ΔP\), and \(E_s < 1\). A good with unitary elasticity of supply has equal percent changes in quantity supplied and price: \(\%ΔQ^s = \%ΔP\), and \(E_s = 1\). Figure \(\PageIndex{3}\) illustrates the different categories of the own price elasticity of supply.
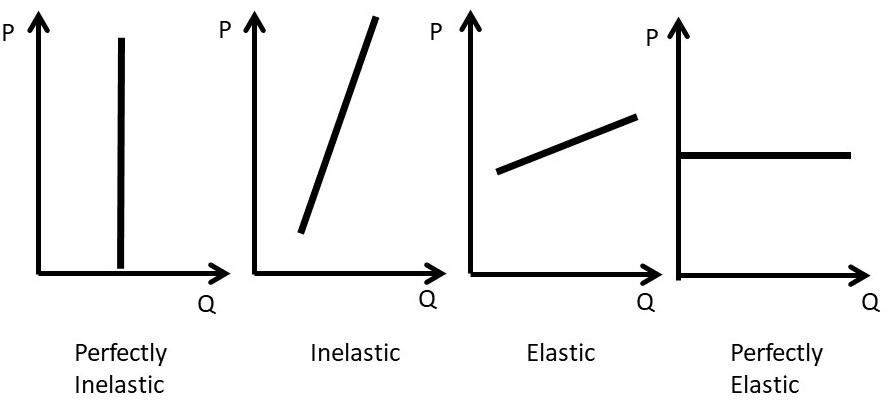
Income Elasticity: Ei
The income elasticity \((E_i)\) measures how consumers of a good respond to a one percent increase in income \((I)\), as shown in Equation /ref{1.11}:
\[E_i = \frac{\%ΔQ^d}{\%ΔI}.\label{1.11}\]
The income elasticity is defined in a similar way as the price elasticities.
Income Elasticity = the percentage change in demand given a one percent change in income, ceteris paribus.
Income elasticities are also categorized into responsiveness classifications. A normal good is one that increases with an increase in income \((E_i > 0)\). There are two subcategories of normal goods: necessities and luxury goods. Notice that necessity goods and luxury goods are normal goods. They represent subgroups of the normal category, since \(E_i\) is positive in both cases.
\[\begin{align*} &\text{Normal Good } & E_i &> 0\\ &\text{Necessity Good} & 0 &< E_i < 1\\ &\text{Luxury Good} & E_i &> 1\\ &\text{Inferior Good} & E_i &< 1\end{align*}\]
The graphs of the relationship between income and demand are called, “Engel Curves,” named for Ernst Engel (1821-1896), a German statistician who first investigated the impact of income on consumption.
A necessity good is a normal good that has a positive, but small, increase in demand given a one percent increase in income. Food is an example, since consumers increase the consumption of food with an increase in income, but the total amount of food consumed reaches an upper limit. This is shown in Figure \(\PageIndex{4}\), left panel.
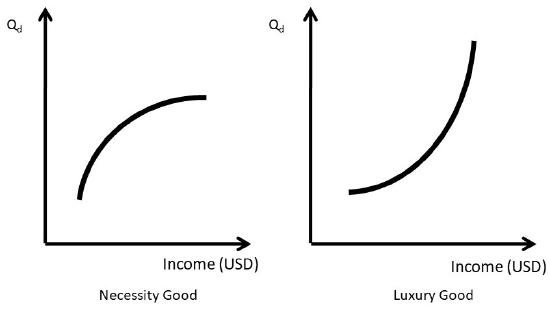
A luxury good is one that has increasing demand as income increases, as shown in the right panel of Figure \(\PageIndex{4}\). Good such as boats, golf club memberships, and expensive clothing are examples of luxury goods. Inferior goods (Figure \(\PageIndex{5}\)) are characterized by lower levels of consumption as income increases: ramen noodles and used clothes are examples.
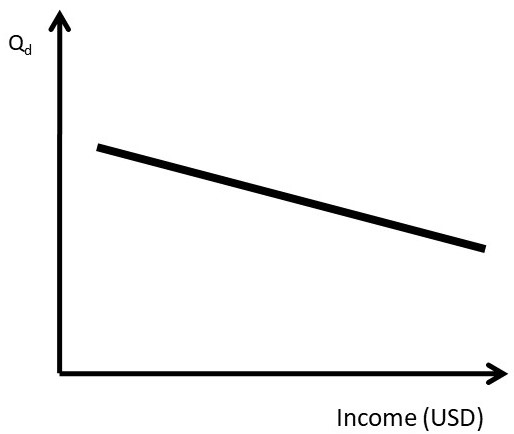
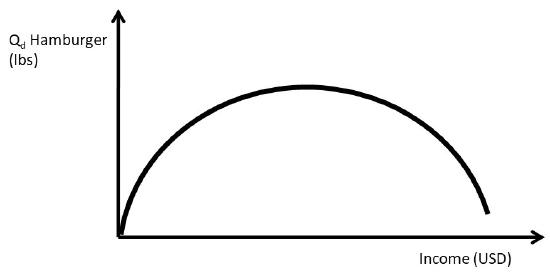
It is important to point out that a good can be a normal good at low income levels, and an inferior good at higher income levels. Hamburger (ground beef) is an example. At low levels of income, hamburger consumption might increase when income rises (Figure \(\PageIndex{6}\)). However, at higher levels of income, consumers might shift out of ground beef and into more expensive meats such as steak. Figure \(\PageIndex{6}\) shows that the same good can be both a normal good and an inferior good, at different levels of income.
Cross Price Elasticity of Demand: Edxy
The cross price elasticity of demand measures the responsiveness of demand for one good with respect to a change in the price of another good.
\[E_{dxy} = \frac{\%ΔQ^d_y}{\%ΔP_x}\label{1.12}\]
Cross Price Elasticity of Demand = the percentage change in the demand of one good given a one percent change in a related good’s price, ceteris paribus.
The cross price elasticity is important for two categories of related goods: substitutes and complements in consumption. Substitutes in consumption will have a positive cross price elasticity of demand, since consumers will decrease purchases of the good that has the price increase, and buy more substitute goods. Complements in consumption are goods that are consumed together, like macaroni and cheese. If the price of macaroni increases, then consumption of both macaroni and cheese decreases.
\[\begin{align*} &\text{Substitutes in Consumption } & E_{dxy} &= \frac{\%ΔQ^d_y}{\%ΔP_x} > 0\\ &\text{Complements in Consumption } & E_{dxy} &= \frac{\%ΔQ^d_y}{\%ΔP_x} < 0\\ &\text{Unrelated Goods in Consumption } & E_{dxy} &= \frac{\%ΔQ^d_y}{\%ΔP_x} = 0 \end{align*}\]
Unrelated goods have a cross price elasticity of demand equal to zero. This is because a change in the price of a good has no effect on the quantity demanded of an unrelated good.
Cross Price Elasticity of Supply: Esxy
The cross price elasticity of supply captures the responsiveness of the supply of one good, given a change in the price of another good.
\[E_{sxy} = \frac{\%ΔQ^s_y}{\%ΔP_x} \label{1.13}\]
Cross Price Elasticity of Supply = the percentage change in the supply of one good given a one percent change in a related good’s price, ceteris paribus.
Substitutes in production are goods that are produced “either/or,” such as corn and soybeans. The same resources (land, machinery, labor, etc.) could be used to produce either corn or soybeans, but the two crops can not be grown on the same land at the same time. The cross price elasticity of supply of substitutes in production is negative. If the price of corn increases, for example, then producers will devote more land to corn and less to soybeans.
\[\begin{align*} &\text{Substitutes in Production } & E_{sxy} &= \frac{\%ΔQ^s_y}{\%ΔP_x} < 0\\ &\text{Complements in Production } & E_{sxy} &= \frac{\%ΔQ^s_y}{\%ΔP_x} > 0\\ &\text{Unrelated Goods in Production } & E_{sxy} &= \frac{\%ΔQ^s_y}{\%ΔP_x} = 0 \end{align*}\]
Complements in production are goods that are produced together, such as beef and leather. Complements in production have a positive cross price elasticity: if the price of beef increases, both more beef and more leather will be supplied to the market. Unrelated goods in production have a cross price elasticity of supply equal to zero, since the price of an unrelated good has no impact on the demand of the other unrelated good.
Price Elasticities and Time
The magnitude of the price elasticity of supply measures how easy it is for the firm to adjust to price changes. In the immediate run (a short time period), the firm can not adjust the production process, so the supply is typically perfectly inelastic. In the short run, a time period when some inputs are fixed and some inputs are variable, the firm may be able to adjust some inputs, so supply is inelastic, but not perfectly inelastic. In the long run, all inputs are variable, and the firm can make adjustments to the production process. In this case, supply is elastic. As more time passes, the price elasticity of supply increases.
This relationship also holds for the price elasticity of demand. If the price of a good increases in the immediate run, there is little consumers can do other than purchase the good. Air travelers who have an emergency that they need to attend to will pay a high price of an airline ticket on the same day of the flight. As time passes, there are more options available to the consumer, and the price elasticity of demand becomes more elastic with the passage of time.
Elasticity of Demand along a Linear Demand Curve
Interestingly, the elasticity of demand changes along a linear demand curve. This is due to the calculation of the own price elasticity of demand as percentage change in quantity demanded caused by a percentage change in the price of the good. In Figure \(\PageIndex{7}\), the slope of the demand function is constant: it does not change over the entire demand curve.
For example, suppose that the inverse demand function is given by: \(P = 10 – Q^d\), where \(P\) is the price of the good and \(Q^d\) is the quantity demanded. In this case, the vertical intercept (y-intercept) is equal to 10, and the slope is equal to negative one. It should be emphasized that, in this case, the slope is constant and equal to minus one for the entire demand curve.
The elasticity of demand, however, changes in value quite dramatically from the y-intercept to the x-intercept. It changes from a value of zero on the x-axis to a value of negative infinity on the y-axis. The cause is the calculation of percentage change.
Consider an example of a mouse and an elephant. If both gain one pound, the weight gain is identical, but the percentage change is vastly different. Suppose that the mouse weighs one-tenth of a pound, the elephant weighs 10,000 pounds, and the total weight gain for both the mouse and the elephant is one pound. The percentage weight gain is \(\%ΔWG = \dfrac{ΔWG}{WG_0}\), where \(ΔWG\) is the change in weight, and \(WG_0\) is the initial weight gain. For the mouse,
\[\%ΔWG \text{ mouse } = \frac{ΔWG}{WG_0} = \frac{1 \text{ lb}}{0.1 \text{ lbs}} = 10 = 1000 \text{ percent!} \label{1.14}\]
For the elephant,
\[\%ΔWG \text{ elephant} = \frac{ΔWG}{WG_0} = \frac{1 \text{ lb}}{10,000 \text{ lbs}} = 0.0001 = 0.01 \text{ percent!} \label{1.15}\]
The take home message of the story is that the total weight gain was identical for both the elephant and the mouse (one pound), whereas the percentage weight gain was enormously different.
This is also true of the elasticity of demand along the linear demand curve. Consider the point where the linear demand curve crosses the x-axis. At this point, the price is equal to zero. Suppose that we raised the price by one unit to find out how responsive consumers are to an increase in price. The price elasticity of demand is:
\[E_d = \frac{\%ΔQ^d}{\%ΔP}.\label{1.16}\]
At the x-intercept, the percentage change in price \((\%ΔP)\) is equal to \(dfrac{ΔP}{P} = \dfrac{1}{0} =\) infinity. The elasticity of demand is equal to the percentage change in quantity demanded \((\%ΔQ)\) divided by the percentage change in price \((\%ΔP =\) infinity). Thus, \(E_d = 0\) at the x-intercept, since dividing any number by infinity is equal to zero.
How responsive are consumers to a change in price at the vertical axis? At the y-intercept, the percentage change in quantity demanded \((\%ΔQ_d)\) is equal to \(\dfrac{ΔQ_d}{Q_d} = \dfrac{1}{0} =\) infinity. Therefore, the elasticity of demand is equal to the percentage change in quantity demanded \((\%ΔQ =\) infinity) divided by the percentage change in price \((\%ΔP)\). Thus, \(\mid E_d\mid =\) infinity at the y-intercept.
At the midpoint, the price elasticity of demand is equal to negative one.
\[E_d = \frac{\%ΔQ^d}{\%ΔP} = \left(\frac{ΔQ^d}{ΔP}\right)\left(\frac{P}{Q^d}\right) = -1 \label{1.17}\]
At the midpoint, the slope of the demand curve is equal to minus one \((\dfrac{ΔQ^d}{ΔP} = 1)\), and the price is equal to the quantity demanded \((P = Q^d)\). Therefore the own price elasticity of demand at the midpoint of a linear demand curve is equal to minus one \(\left(\dfrac{ΔQ^d}{ΔP}\right)\left(\dfrac{P}{Q_d}\right) = -1\).
A valuable lesson is learned in this example: be careful to distinguish between the slope of a demand curve and the elasticity of demand. When interpreting graphs, the slope is not a good determinant of elasticity, since a graph could be drawn steep or shallow depending on the units. The elasticity is related to the slope, but it is not equal to the slope!
Agricultural Policy Example of Elasticity of Demand
The impact of agricultural policies depends critically on the elasticity of demand. It was claimed earlier that the price elasticity of demand is the most important thing that a business firm can know. This section provides evidence of the importance of the price elasticity of demand. The own price elasticity of demand for food is inelastic in a domestic economy with no trade. Everyone must eat, and the caloric intake will not be greatly influenced by the price of food.
This changes enormously in a global economy. In an open economy that has international trade, there are many overseas customers for food exports, and many competing nations that export food. For example, the US is a major wheat exporter. Other wheat exporting nations include: Canada, Australia, Argentina, the European Union (EU), and many of the former Soviet nations in Eastern Europe such as Ukraine. In this case, the US faces a highly elastic demand for wheat in the global economy: if the US increased the price of wheat above the world price, wheat importers would shift purchases from the US to other wheat exporters. A global economy changes the effectiveness of price policies enormously.
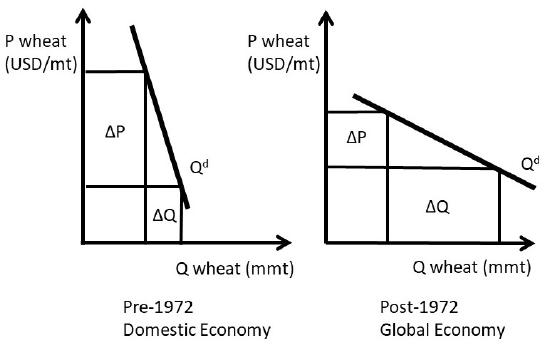
Prior to 1972, the United States agricultural sector could be characterized as a domestic economy, with less food and agricultural trade. In this case, the demand for food was primarily domestic, and thus relatively inelastic (Figure \(\PageIndex{8}\), left panel).
Starting in 1933, agricultural price supports increased the price of wheat above the market equilibrium level. This policy worked well, as long as the surplus was eliminated. One way to eliminate the surplus was through acreage restrictions, which limited the number of acres planted to wheat (\(ΔQ\) in the left panel of Figure \(\PageIndex{8}\)). Acreage limitations and production quotas were used to decrease the quantity of wheat in the market. These policies worked well prior to 1972, since the US agricultural economy was primarily domestic, characterized by an inelastic demand curve. The decrease in quantity led to a larger increase in price \((ΔP > ΔQ^d)\), given the inelastic demand in a domestic economy.
In 1972, major changes in international exchange rate policies, together with poor weather in Asia, led to the globalization of US food and agricultural markets. A larger percentage of the US wheat crop was exported, and the inelastic demand that prevailed prior to 1972 became more elastic in the globalized environment (right panel, Figure \(\PageIndex{8}\)). Although the wheat market became globalized, the policies did not. During the 1980s, the US maintained price supports and production controls in the seven basic commodities (defined by the USDA as: wheat, corn, sorghum, sugar, cotton, rice, and tobacco). These policies were counterproductive, as they priced the grain out of the world market. The US attempted to increase the market share of wheat trade, only to find that the US price was higher than the other major wheat exporters.
Figure \(\PageIndex{8}\) shows why the policies implemented in 1933 were hurting more than they were helping. Production controls were decreasing the quantity of wheat. In the domestic economy (left panel of Figure \(\PageIndex{8}\), pre-1970), this achieved the objectives of the policies: wheat producer were made better off, since the increase in price was greater than the decrease in quantity. This all changed in the globalized world after 1972 (right panel of Figure \(\PageIndex{8}\), post 1972). With an elastic demand, the decrease in quantity did not result in large price increases. Price supports raised the US price above the world price of wheat. These policies were not working, and in 1996, they were changed to make the US grain industry more competitive in the global market. Today, a large fraction of all grain produced in the US is exported.
In summary, policies intended to help producers have greatly divergent outcomes, depending on the price elasticity of demand. In a domestic economy, the demand for food and agricultural products is typically inelastic. In this case, production controls and price supports will achieve the policy goal of helping producers: the price increases will be larger than the quantity decreases (left panel, Figure \(\PageIndex{8}\)). In a global economy, the demand for food and agricultural goods is elastic: there are many nations that export grains (right panel, Figure \(\PageIndex{8}\)). In this case the policy that helps producers the most is technological change, which will shift the supply curve to the right. With an elastic demand, the increase in quantity is larger than the decrease in price.
This is the same strategy that Walmart utilizes: everyday low prices. Sam Walton found that the increase in sales due to low prices more than offset the decrease in price \((ΔQ^d > ΔP)\). This is true in any market characterized by an elastic demand. Since most consumer goods in the United States have many substitutes, Walton’s lower-price strategy led to Walmart becoming the most successful retailer in the history of the world.
Calculation of Market Supply and Demand Elasticities
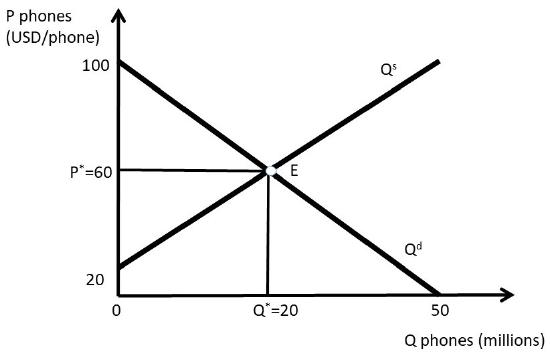
In Section 1.3.4 above, inverse supply and demand curves were used to calculate the equilibrium price and quantity of phones.
The inverse demand and supply functions were:
\[P = 100 – 2Q^d \label{1.18}\]
\[P = 20 + 2Q^s \label{1.19}\]
Where \(P\) is the price of phones in USD/unit, and \(Q\) is the quantity of phones in millions. By setting the two equations equal to each other, the intersection of the inverse supply and demand curves was found, yielding the equilibrium market price and quantity:
\[P^e = \text{ USD } 60\text{/phones,}\]
and
\[Q^e = 20 \text{ million phones.}\]
The graph of the phone market is replicated in Figure \(\PageIndex{9}\).
To calculate the own price elasticities of supply and demand, simple calculus provides an easy solution. Recall the definition of the own price elasticity of demand:
\[E_d = \frac{\%ΔQ^d}{\%ΔP} = \left(\frac{ΔQ_d}{ΔP}\right)\left(\frac{P}{Q_d}\right) = \left(\frac{∂Q_d}{∂P}\right)\left(\frac{P}{Q_d}\right)\label{1.20}\]
The delta sign \((Δ)\) refers to a small change in a variable. This is the same as the derivative sign, “\(∂\).” The difference is that the derivative indicates in infinitesimally small change, whereas the delta sign is a discrete change, which is the same idea, just larger. Therefore, the delta signs can be replaced with the derivative signs in the equation that defines the price elasticity of demand. For example, the slope of a function is \(\dfrac{Δy}{Δx}\). The slope of the function at a given point on the function is \(\dfrac{∂y}{∂x}\).
The last expression in the equation shows that to calculate \(E_d\), use the derivative of quantity with respect to price, and the levels of \(P\) and \(Q\). At the equilibrium point, the equilibrium levels of \(P\) and \(Q\) are known. To find the derivative, begin by taking the derivative of the inverse demand equation (Equation \ref{1.18}).
\[\frac{∂P}{∂Q^d} = – 2\label{1.21}\]
This is simply the power function rule from calculus [if \(y =ax^b\), then \(\dfrac{∂y}{∂x} = abx^{b-1}\)]. Notice something important: the derivative of the inverse demand equation is the inverse of what is needed to calculate the price elasticity. This is due to the inverse demand function being, “price-dependent,” with \(P\) on the left hand side. To find the derivative \(\dfrac{∂Q^d}{∂P}\), invert the derivative by dividing one by the derivative.
\[\frac{∂Q^d}{∂P} = –\left(\frac{1}{2}\right) \label{1.22}\]
\[E_d = \frac{\%ΔQ^d}{\%ΔP} = \left(\frac{ΔQ^d}{ΔP}\right)\left(\frac{P}{Q^d}\right) = \left(\frac{∂Q^d}{∂P}\right)\left(\frac{P}{Q^d}\right) = -\left(\frac{1}{2}\right)\left(\frac{60}{20}\right) = -1.5\label{1.23}\]
The absolute value of the own price elasticity of demand at the equilibrium point is:
\(\mid E_d\mid = 1.5\). The demand for phones is elastic: if the price were increased one percent, the decrease in phone purchases would be 1.5 percent.
The own price elasticity of supply can be found using the same procedure:
\[E_s = \frac{\%ΔQ^s}{\%ΔP} = \left(\frac{ΔQ^s}{ΔP}\right)\left(\frac{P}{Q^s}\right) = \left(\frac{∂Q^s}{∂P}\right)\left(\frac{P}{Q^s}\right)\label{1.24}\]
First, take the derivative of the inverse supply function (Equation \ref{1.19}).
\[\frac{∂P}{∂Q^s} = + 2 \label{1.25}\]
Invert this derivative to find the derivative needed to calculate the price elasticity of supply:
\[\frac{∂Q^s}{∂P} = + \left(\frac{1}{2}\right). \label{1.26}\]
Then plug in the ingredients of the own price elasticity of supply:
\[E_s = \frac{\%ΔQ^s}{\%ΔP} = \left(\frac{ΔQ^s}{ΔP}\right)\left(\frac{P}{Q^s}\right) = \left(\frac{∂Q^s}{∂P}\right)\left(\frac{P}{Q^s}\right) = \left(\frac{1}{2}\right)\left(\frac{60}{20}\right) = 1.5 \label{1.27}\]
The price elasticity of supply is also elastic: a one percent increase in price results in a 1.5 percent increase in the quantity supplied of phones.
Two points are worth mentioning here. First, the price elasticities of supply and demand are not always symmetrical, as they are in this case (-1.5 and +1.5). The elasticities depend on the shape of the inverse supply and demand functions. The symmetry of the functions used here can be seen in Figure \(\PageIndex{9}\). When the inverse supply and demand functions are not symmetrical, the absolute values of the elasticities will be of different magnitudes. The second important point concerns the use of inverse supply and demand functions. The inverse functions are used to align with the “backwards” nature of the supply and demand graphs: price is the independent variable, but appears on the vertical axis. To find the derivative needed to calculate the price elasticities, the procedure above first took the derivative of the inverse function, then inverted it to achieve \(\dfrac{∂Q}{∂P}\). This derivative could also be found be first, inverting the inverse function to get the quantity isolated on the left hand side, then taking the derivative. This alternative procedure will result in the same elasticity calculation as the one used above. To test your knowledge, try this procedure to double check your answers!


