9.6: 9.2 Managing the Budget -- Project Management for Instructional Designers
- Page ID
- 39864
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)9.2 Managing the Budget
Visit Audio Recordings for the audio version of this section.
LEARNING OBJECTIVES
- Describe methods to manage cash flow.
- Describe the terms and relationships of budget factors used in earned value analysis.
- Calculate and interpret budget and schedule variances.
- Calculate and interpret the schedule performance index and the cost performance index.
- Calculate and interpret estimates to complete the project.
- Calculate the revised final budget.
Projects seldom go according to plan in every detail. It is necessary for the project manager to be able to identify when costs are varying from the budget and to manage those variations.
MANAGING CASH FLOW
If the total amount spent on a project is equal to or less than the amount budgeted, the project can still be in trouble if the funding for the project is not available when it is needed. There is a natural tension between the financial people in an organization, who do not want to pay for the use of money that is just sitting in a checking account, and the project manager, who wants to be sure that there is enough money available to pay for project expenses. The financial people prefer to keep the company’s money working in other investments until the last moment before transferring it to the project account. The contractors and vendors have similar concerns, and they want to get paid as soon as possible so they can put the money to work in their own organizations. The project manager would like to have as much cash available as possible to use if activities exceed budget expectations.
Contingency Reserves
Most projects have something unexpected occur that increases costs above the original estimates. If estimates are rarely exceeded, the estimating method should be reviewed because the estimates are too high. It is impossible to predict which activities will cost more than expected, but it is reasonable to assume that some of them will. Estimating the likelihood of such events is part of risk analysis, which is discussed in more detail in a later chapter.
Instead of overestimating each cost, money is budgeted for dealing with unplanned but statistically predictable cost increases. Funds allocated for this purpose are called contingency reserves.1 Because it is likely that this money will be spent, it is part of the total budget for the project. If this fund is adequate to meet the unplanned expenses, then the project will complete within the budget.
Management Reserves
If something occurs during the project that requires a change in the project scope, money may be needed to deal with the situation before a change in scope can be negotiated with the project sponsor or client. It could be an opportunity as well as a challenge. For example, if a new technology were invented that would greatly enhance your completed project, there would be additional cost and a change to the scope, but it would be worth it. Money can be made available at the manager’s discretion to meet needs that would change the scope of the project. These funds are called management reserves. Unlike contingency reserves, they are not likely to be spent and are not part of the project’s budget baseline, but they can be included in the total project budget.2
Evaluating the Budget During the Project
A project manager must regularly compare the amount of money spent with the budgeted amount and report this information to managers and stakeholders. It is necessary to establish an understanding of how this progress will be measured and reported.
Reporting Budget Progress on John’s Move
As John’s friend points out, a budget report must compare the amount spent with the amount that is expected to be spent by that point in the project. Basic measures such as percentage of activities completed, percentage of measurement units completed, and percentage of budget spent are adequate for less complex projects, but more sophisticated techniques are used for projects with higher complexity.
EARNED VALUE ANALYSIS
A method that is widely used for medium- and high-complexity projects is the earned value management (EVM) method. EVM is a method of periodically comparing the budgeted costs with the actual costs during the project. It combines the scheduled activities with detailed cost estimates of each activity. It allows for partial completion of an activity if some of the detailed costs associated with the activity have been paid but others have not.
The budgeted cost of work scheduled (BCWS) comprises the detailed cost estimates for each activity in the project. The amount of work that should have been done by a particular date is the planned value (PV). These terms are used interchangeably by some sources, but the planned value term is used in formulas to refer to the sum of the budgeted cost of work up to a particular point in the project, so we will make that distinction in the definitions in this text for clarity.
Planned Value on Day Six of John’s Move
Figure 9.6 Planned Value for Lunch and Packing Materials
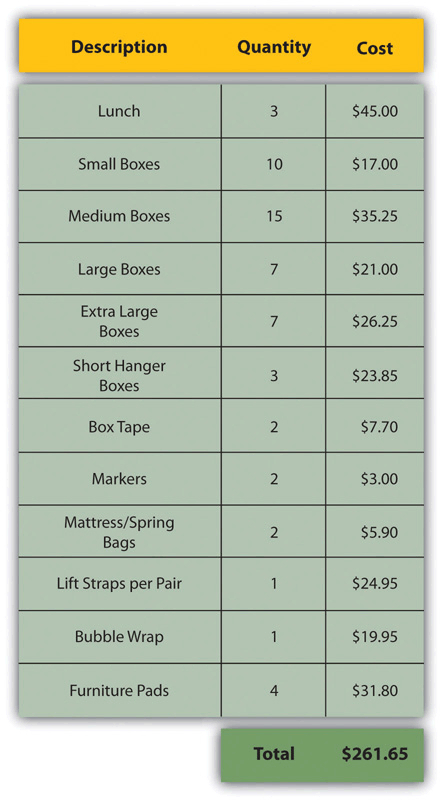
The budgeted cost of work performed (BCWP) is the budgeted cost of work scheduled that has been done. If you sum the BCWP values up to that point in the project schedule, you have the earned value (EV). The amount spent on an item is often more or less than the estimated amount that was budgeted for that item. The actual cost (AC) is the sum of the amounts actually spent on the items.
Comparing PV, EV, and AC in John’s Move on Day Six
Figure 9.7 Planned Value, Earned Value, and Actual Cost
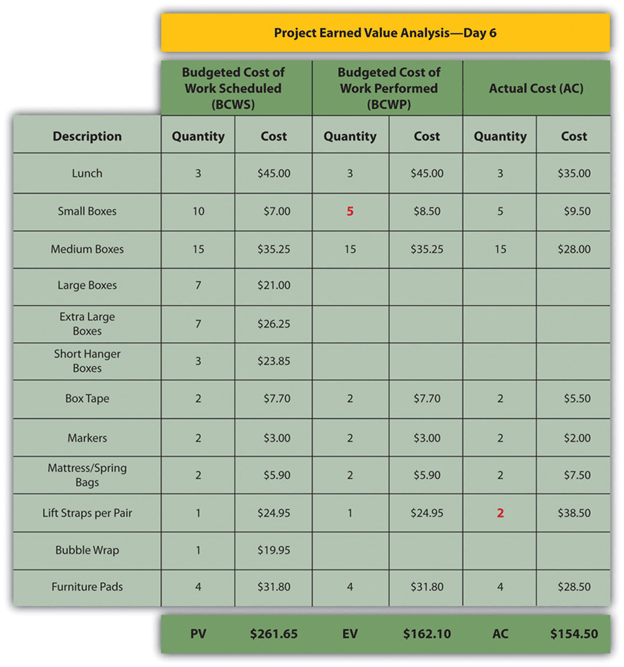
The original schedule called for spending $261.65 (PV) by day six. The amount of work done was worth $162.10 (EV) according to the estimates, but the actual cost was only $154.50 (AC).
SCHEDULE VARIANCE
The project manager must know if the project is on schedule and within the budget. The difference between planned and actual progress is the variance. The schedule variance (SV) is the difference between the earned value (EV) and the planned value (PV). Expressed as a formula, SV = EV − PV. If less value has been earned than was planned, the schedule variance is negative, which means the project is behind schedule.
Schedule Variance on John’s Move
The difference between the earned value (EV) and the actual cost (AC) is the cost variance (CV). Expressed as a formula, CV = EV – AC. A positive CV indicates the project is under budget.
Cost Variance on John’s Move
Variance Indexes for Schedule and Cost
The schedule variance and the cost variance provide the amount by which the spending is behind (or ahead of) schedule and the amount by which a project is exceeding (or less than) its budget. They do not give an idea of how these amounts compare with the total budget.
The ratio of earned value to planned value gives an indication of how much of the project is completed. This ratio is the schedule performance index (SPI). The formula is SPI = EV/PV. In the John’s move example, the SPI equals 0.62 (SPI = $162.10/$261.65 = 0.62) A SPI value less than one indicates the project is behind schedule.
The ratio of the earned value to the actual cost is the cost performance index (CPI). The formula is CPI = EV/AC.
Cost Performance Index of John’s Move
In the John’s move example, CPI = $162.10/$154.50 = 1.05 A value greater than 1 indicates the project is under budget.
Figure 9.8 Schedule Variance and Cost Variance on Day Six of the John’s Move Project
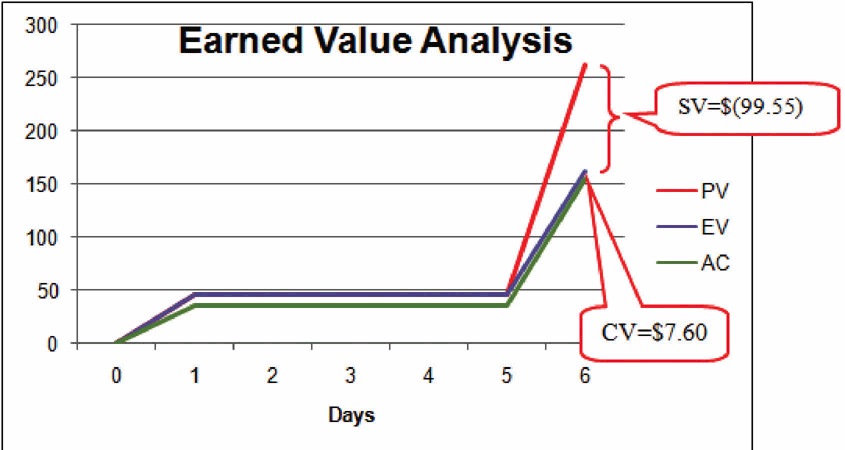
The cost variance of positive $7.60 and the CPI value of 1.05 tell John that he is getting more value for his money than planned for the tasks scheduled by day six. The schedule variance (SV) of negative $99.55 and the schedule performance index (SPI) of 0.62 tell him that he is behind schedule in adding value to the project.
During the project, the manager can evaluate the schedule using the schedule variance (SV) and the schedule performance index (SPI) and the budget using the cost variance (CV) and the cost performance index (CPI).
ESTIMATED COST TO COMPLETE THE PROJECT
Partway through the project, the manager evaluates the accuracy of the cost estimates for the activities that have taken place and uses that experience to predict how much money it will take to complete the unfinished activities of the project—the estimate to complete (ETC).
To calculate the ETC, the manager must decide if the cost variance observed in the estimates to that point are representative of the future. For example, if unusually bad weather causes increased cost during the first part of the project, it is not likely to have the same effect on the rest of the project. If the manager decides that the cost variance up to this point in the project is atypical—not typical—then the estimate to complete is the difference between the original budget for the entire project—the budget at completion (BAC)—and the earned value (EV) up to that point. Expressed as a formula, ETC = BAC − EV
Estimate to Complete John’s Move
If the manager decides that the cost variance is caused by factors that will affect the remaining activities, such as higher labor and material costs, then the estimate to complete (ETC) needs to be adjusted by dividing it by the cost performance index (CPI). For example, if labor costs on the first part of a project are estimated at $80,000 (EV) and they actually cost $85,000 (AC), the cost variance will be 0.94. (Recall that the cost variance = EV/AC).
To calculate the estimate to complete (ETC) assuming the cost variance on known activities is typical of future cost, the formula is ETC = (BAC – EV)/CPI. If the budget at completion (BAC) of the project is $800,000, the estimate to complete is ($800,000 – $80,000)/0.94 = $766,000.
ESTIMATE FINAL PROJECT COST
If the costs of the activities up to the present vary from the original estimates, it will affect the total estimate for the project cost. The new estimate of the project cost is the estimate at completion (EAC). To calculate the EAC, the estimate to complete (ETC) is added to the actual cost (AC) of the activities already performed. Expressed as a formula, EAC = AC + ETC.
Estimate at Completion for John’s Move
Refer to Figure 9.9 for a summary of terms and formulas.
Figure 9.9 Summary of Terms and Formulas for Earned Value Analysis
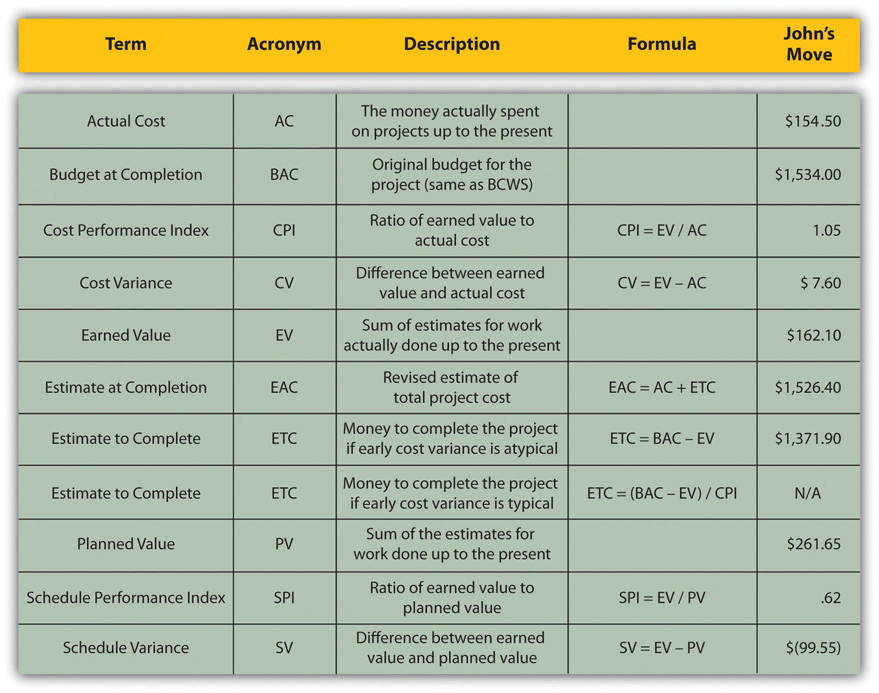
KEY TAKEAWAYS
- Extra money is allocated in a contingency fund to deal with activities where costs exceed estimates. Funds are allocated in a management reserves in case a significant opportunity or challenge occurs that requires change of scope but funds are needed immediately before a scope change can typically be negotiated.
- Schedule variance is the difference between the part of the budget that has been done so far (EV) versus the part that was planned to be completed by now (PV). Similarly, the cost variance is the difference between the EV and the actual cost (AC).
- The schedule performance index (SPI) is the ratio of the earned value and the planned value. The cost performance index (CPI) is the ratio of the earned value (EV) to the actual cost (AC).
- The formula used to calculate the amount of money needed to complete the project (ETC) depends on whether or not the cost variance to this point is expected to continue (typical) or not (atypical). If the cost variance is atypical, the ETC is simply the original total budget (BAC) minus the earned value (EV). If they are typical of future cost variances, the ETC is adjusted by dividing the difference between BAC and EV by the CPI.
- The final budget is the actual cost (AC) to this point plus the estimate to complete (ETC).
[1] Project Management Institute, Inc., A Guide to the Project Management Body of Knowledge (PMBOK Guide), 4th ed. (Newtown Square, PA: Project Management Institute, Inc., 2008), 173.
[2] Project Management Institute, Inc., A Guide to the Project Management Body of Knowledge (PMBOK Guide), 4th ed. (Newtown Square, PA: Project Management Institute, Inc., 2008), 177.


