3.2: Operationalization
- Last updated
- Save as PDF
- Page ID
- 81910
The discussion so far has shown some of the practical challenges posed even by a simple construct like VARIETY with seemingly obvious values such as BRITISH and AMERICAN. However, there is a more fundamental, and more challenging issue to consider: As hinted at in Section 3.1.1, we are essentially making (sets of) existential statements when we postulate such constructs. All examples discussed above simply assumed the existence of something called “British English” and “American English”, concepts that in turn presuppose the existence of something called “English” and of the properties “British” and “American”. But if we claim the existence of these constructs, we must define them; what is more, we must define them in a way that enables us (and others) to find them in the real world (in our case, in samples of language use). We must provide what is referred to as operational definitions.
3.2.1 Operational definitions
Put simply, an operational definition of a construct is an explicit and unambiguous description of a set of operations that are performed to identify and measure that construct. This makes operational definitions fundamentally different from our every-day understanding of what a definition is.
Take an example from physics, the property HARDNESS. A typical dictionary definition of the word hard is the following (the abbreviations refer to dictionaries, see Study Notes to the current chapter):
(15) 1 FIRM TO TOUCH firm, stiff, and difficult to press down, break, or cut [≠ soft] (LDCE, s.v. hard, cf. also the virtually identical definitions in CALD, MW and OALD)
This definition corresponds quite closely to our experiential understanding of what it means to be hard. However, for a physicist or an engineer interested in the hardness of different materials, it is not immediately useful: firm and stiff are simply loose synonyms of hard, and soft is an antonym – they do not help in understanding hardness, let alone in finding hardness in the real world. The remainder of the definition is more promising: it should be possible to determine the hardness of a material by pressing it down, breaking or cutting it and noting how difficult this is. However, before, say, “pressing down” can be used as an operational definition, at least three questions need to be asked: first, what type of object is to be used for pressing (what material it is made of and what shape it has); second, how much pressure is to be applied; and third, how the “difficulty” of pressing down is to be determined.
There are a number of hardness tests that differ mainly along the answers they provide to these questions (cf. Herrmann (2011) and Wiederhorn et al. (2011) for a discussion of hardness tests). One commonly used group of tests is based on the size of the indentation that an object (the “indenter”) leaves when pressed into some material. One such test is the Vickers Hardness Test, which specifies the indenter as a diamond with the shape of a square-based pyramid with an angle of 136°, and the test force as ranging between or 49.3 to 980.7 newtons (the exact force must be specified every time a measurement is reported). Hardness is then defined as follows (cf. Herrmann 2011: 43):
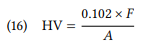
F is the load in newtons, A is the surface of the indentation, and 0.102 is a constant that converts newtons into kilopond (this is necessary because the Vickers Hardness Test used to measure the test force in kilopond before the newton became the internationally recognized unit of force).
Unlike the dictionary definition quoted above, Vickers Hardness (HV) is an operational definition of hardness: it specifies a procedure that leads to a number representing the hardness of a material. This operational definition is partly motivated by our experiential understanding of hardness in the same way as (part of) the dictionary definition (“difficult to press down”), but in other aspects, it is arbitrary. For example, one could use indenters that differ in shape or material, and indeed there are other widely used tests that do this: the Brinell Hardness Test uses a hardmetal ball with a diameter that may differ depending on the material to be tested, and the Knoop Hardness Test uses a diamond indenter with a rhombic-based pyramid shape. One could also use a different measure of “difficulty of pressing down”: for example, some tests use the rebound energy of an object dropped onto the material from a particular height.
Obviously, each of these tests will give a different result when applied to the same material, and some of them cannot be applied to particular materials (for example, materials that are too flexible for the indenter to leave an indentation, or materials that are so brittle that they will fracture during testing). More crucially, none of them attempt to capture the “nature” of hardness; instead, they are meant to turn hardness into something that is close enough to our understanding of what it means to be hard, yet at the same time reliably measurable.
Take another example: in psychiatry, it is necessary to identify mental disorders in order to determine what (if any) treatment may be necessary for a given patient. But clearly, just like the hardness of materials, mental disorders are not directly accessible. Consider, for example, the following dictionary definition of schizophrenia:
(17) a serious mental illness in which someone cannot understand what is real and what is imaginary [CALD, s.v. schizophrenia, see again the very similar definitions in LDCE, MW and OALD].
Although matters are actually substantially more complicated, let us assume that this definition captures the essence of schizophrenia. As a basis for diagnosis, it is useless. The main problem is that “understanding what is real” is a mental process that cannot be observed or measured directly (a second problem is that everyone may be momentarily confused on occasion with regard to whether something is real or not, for example, when we are tired or drunk).
In psychiatry, mental disorders are therefore operationally defined in terms of certain behaviors. For example, the fourth edition of the Diagnostic and Statistical Manual of Mental Disorders (DSM-IV), used by psychiatrists and psychologists in the United States to diagnose schizophrenia, classifies an individual as schizophrenic if they (i) display at least two of the following symptoms: “delusions”, “hallucinations”, “disorganized speech”, “grossly disorganized or catatonic behavior” and “affective flattening”, “poverty of speech” or “lack of motivation”; and if they (ii) function “markedly below the level achieved prior to the onset” in areas “such as work, interpersonal relations, or self-care”; and if (iii) these symptoms can be observed over a period of at least one month and show effects over a period of at least six months; and if (iv) similar diagnoses (such as schizoaffective disorder) and substance abuse and medication can be ruled out (APA 2000).
This definition of schizophrenia is much less objective than that of physical hardness, which is partly due to the fact that human behavior is more complex and less comprehensively understood than the mechanical properties of materials, and partly due to the fact that psychology and psychiatry are less mature disciplines than physics. However, it is an operational definition in the sense that it effectively presents a check-list of observable phenomena that is used to determine the presence of an unobservable phenomenon. As in the case of hardness tests, there is no single operational definition – the International Statistical Classification of Diseases and Related Health Problems used by European psychologists and psychiatrists offers a different definition that overlaps with that of the DSM-IV but places more emphasis on (and is more specific with respect to) mental symptoms and less emphasis on social behaviors.
As should have become clear, operational definitions do not (and do not attempt to) capture the “essence” of the things or phenomena they define. We cannot say that the Vickers Hardness number “is” hardness or that the DSM-IV list of symptoms “is” schizophrenia. They are simply ways of measuring or diagnosing these phenomena. Consequently, it is pointless to ask whether operational definitions are “correct” or “incorrect” – they are simply useful in a particular context. However, this does not mean that any operational definition is as good as any other. A good operational definition must have two properties: it must be reliable and valid.
A definition is reliable to the degree that different researchers can use it at different times and all get the same results; this objectivity (or at least intersubjectivity) is one of the primary motivations for operationalization in the first place. Obviously, the reliability of operational definitions will vary depending on the degree of subjective judgment involved: while Vickers Hardness is extremely reliable, depending only on whether the apparatus is in good working order and the procedure is followed correctly, the DSM-IV definition of schizophrenia is much less reliable, depending, to some extent irreducibly, on the opinions and experience of the person applying it. Especially in the latter case it is important to test the reliability of an operational definition empirically, i.e. to let different people apply it and see to what extent they get the same results (see further Chapter 4).
A definition is valid to the degree that it actually measures what it is supposed to measure. Thus, we assume that there are such phenomena as “hardness” or “schizophrenia” and that they may be more or less accurately captured by an operational definition. Validity is clearly a very problematic concept: since phenomena can only be measured by operational definitions, it would be circular to assess the quality of the same definitions on the basis of these measures. One indirect indication of validity is consistency (e.g., the phenomena identified by the definition share a number of additional properties not mentioned in the definition), but to a large extent, the validity of operationalizations is likely to be assessed on the basis of plausibility arguments. The more complex and the less directly accessible a construct is, the more problematic the concept of validity becomes: While everyone would agree that there is such a thing as HARDNESS, this is much less clear in the case of SCHIZOPHRENIA: it is not unusual for psychiatric diagnoses to be reclassified (for example, what was Asperger’s syndrome in the DSM-IV became part of autism spectrum disorder in the DSM-V) or to be dropped altogether (as was the case with homosexuality, which was treated as a mental disorder by the DSM-II until 1974). Thus, operational definitions may create the construct they are merely meant to measure; it is therefore important to keep in mind that even a construct that has been operationally defined is still just a construct, i.e. part of a theory of reality rather than part of reality itself.
3.2.2 Examples of operationalization in corpus linguistics
Corpus linguistics is no different from other scientific disciplines: it is impossible to conduct any corpus-based research without operational definitions. However, this does not mean that researchers are necessarily aware that this is what they are doing. In corpus-based research, we find roughly three different situations:
- operational definitions may already be part of the corpus and be accepted (more or less implicitly) by the researcher, as is frequently the case with tokenization (which constitutes an operational definition of token that presupposes a particular theory of what constitutes a word), or with part-of-speech tagging (which constitutes an operational definition of word classes), but also with metadata, including the corpus design itself (which typically constitutes a series of operational definitions of language varieties)
- operational definitions may remain completely implicit, i.e. the researcher simply identifies and categorizes phenomena on the basis of their (professional but unspoken) understanding of the subject matter without any indication as to how they proceeded;
- operational definitions and the procedure by which they have been applied may be explicitly stated.
There may be linguistic phenomena, whose definition is so uncontroversial that it seems justified to simply assume and/or apply it without any discussion at all – for example, when identifying occurrences of a specific word like sidewalk. But even here, it is important to state explicitly which orthographic strings were searched for and why. As soon as matters get a little more complex, implicitly applied definitions are unacceptable because unless we state exactly how we identified and categorized a particular phenomenon, nobody will be able to interpret our results correctly, let alone reproduce or replicate them or transfer them to a different set of data.
For example, the English possessive construction is a fairly simple and uncontroversial grammatical structure. In written English it consists either of the sequence [NOUN1 + ’ + s + zero or more ADJECTIVEs + NOUN2] (where the en[1]tire noun phrase that includes NOUN1 is part of the construction) , or [NOUN1 + ’ + zero or more ADJECTIVEs + NOUN2] (if the noun ends in s and is not a surname), or [POSS. PRONOUN + zero or more ADJECTIVEs + NOUN]. These sequences seem easy enough to identify in a corpus (or in a list of hits for appropriately constructed queries), so a researcher studying the possessive may not even mention how they defined this construction. The following examples show that matters are more complex, however:
(18) a. We are a women’s college, one of only 46 women’s colleges in the United States and Canada (womenscollege.du.edu)
b. That wasn’t too far from Fifth Street, and should allow him to make Scotty’s Bar by midnight. (BROWN L05)
c. My Opera was the virtual community for Opera web browser users. (Wikipedia, s.v. My Opera)
d. ‘Oh my God!’ she heard Mike mutter under his breath, and she laughed at his discomfort. (BNC HGM)
e. The following day she caught an early train from King’s Cross station and set off on the two-hundred-mile journey north. (BNC JXT)
f. The true tack traveller would spend his/her honeymoon in a motel, on a heart-shaped water bed. (BNC AAV)
While all of these cases have the form of the possessive construction and match the strings above, opinions may differ on whether they should be included in a sample of English possessive constructions. Example (18a) is a so-called possessive compound, a lexicalized possessive construction that functions like a conventional compound and could be treated as a single word. In examples (18b and c), the possessive construction is a proper name. Concerning the latter: if we want to include it, we would have to decide whether also to include proper names where possessive pronoun and noun are spelled as a single word, as in MySpace (the name of an online social network now lost in history). Example (18d) is similar in that my God is used almost like a proper name; in addition, it is part of a fixed phrase. Example (18e) is a geographical name; here, the problem is that such names are increasingly spelled without an apostrophe, often by conscious decisions by government institutions (see Swaine 2009; Newman 2013). If we want to include them, we have to decide whether also to include spellings without the apostrophe (such as 19), and how to find them in the corpus:
(19) His mother’s luggage had arrived at Kings Cross Station in London, and of course nobody collected it. (BNC H9U)
Finally, (18f) is a regular possessive construction, but it contains two pronouns separated by a slash; we would have to decide whether to count these as one or as two cases of the construction.
These are just some of the problems we face even with a very simple grammatical structure. Thus, if we were to study the possessive construction (or any other structure), we would have to state precisely which potential instances of a structure we include. In other words, our operational definition needs to include a list of cases that may occur in the data together with a statement of whether – and why – to include them or not.
Likewise, it may be plausible in certain contexts to use operational definitions already present in the data without further discussion. If we accept graphemic or even orthographic representations of language (which corpus linguists do, most of the time), then we also accept some of the definitions that come along with orthography, for example concerning the question what constitutes a word. For many research questions, it may be irrelevant whether the orthographic word correlates with a linguistic word in all cases (whether it does depends to a large extent on the specific linguistic model we adopt), so we may simply accept this correspondence as a pre-theoretical fact. But there are research questions, for example concerning the mean length of clauses, utterances, etc., where this becomes relevant and we may have to define the notion of word in a different way. At the very least, we should acknowledge that we are accepting a graphemic or orthographic definition despite the fact that it may not have a linguistic basis.
Similarly, there may be situations where we simply accept the part-of-speech tagging or the syntactic annotation in a corpus, but given that there is no agreed-upon theory of word classes, let alone of syntactic structures, this can be problematic in some situations. At the very least, it is crucial to understand that tagging and other kinds of annotation are the result of applying operational definitions by other researchers and if we use tags or other forms of annotation, we must familiarize ourselves with these definitions by reading the fine manuals that typically accompany the corpus. These manuals and other literature provided by corpus creators must be read and cited like all other literature, and we must clarify in the description of our research design why and to what extent we rely on the operationalizations described in these materials.
Let us look at five examples of frequently used corpus linguistic operationalizations that demonstrate various aspects of the issues sketched out above.
3.2.2.1 Parts of speech
Let us begin with a brief discussion of tokenization and part-of-speech (POS) tagging, two phenomena whose operational definitions are typically decided on and applied by the corpus makers and implicitly accepted by the researchers using a corpus. We saw an example of POS tagging in Figure 2.4 in Chapter 2, but let us look at examples from different corpora. Examples (20a–c) are taken from the BROWN, LOB and FROWN corpora, which share a common corpus design in order to be used comparatively, examples (20d) is from the British National Corpus (the POS tags are shown separated from the word by a slash for consistency, they are encoded in the actual corpora in very different ways):
(20) a. a/AT young/JJ man/NN doesn't/DOZ* like/VB to/TO be/BE driven/VBN up/RP in/IN front/NN of/IN a/AT school/NN in/IN a/AT car/NN driven/VBN by/IN a/AT girl/NN who/WPS isn't/BEZ* even/RB in/IN a/AT higher/JJR class/NN than/CS he/PPS is/BEZ ,/, and/CC is/BEZ also/RB a/AT girl/NN ./. (BROWN A30)
b. none/PN of/IN these/DTS wines/NNS should/MD cost/VB much/RB over/RB 8/CD s/NNU per/IN bottle/NN ,/, but/CC do/DO n't/XNOT roast/VB them/PP3OS in/IN front/IN" of/IN" the/ATI fire/NN ./. (LOB E19)
c. Someone/PN1 had/VVHD to/TO give/VVI Marie/NP1 a/AT1 hand/NN1 down/RP ,/YCOM but/CCB she/PPHS1 did/VADD n't/XX feel/VVI like/II asking/VVG for/IF help/NN1 in/II31 front/II32 of/II33 the/AT still/JJ assembled/JJ press/NN1 ./YSTP (FLOB P26)
d. What/DTQ I/PNP feel/VVB you/PNP are/VBB saying/VVG to/PRP me/PNP is/VBZ that/CJT this/DT0 previous/AJ0 relationship/NN1 is/VBZ something/PNI you/PNP do/VDB n't/XX0 want/VVI to/TO0 talk/VVI about/PRP in/PRP front/NN1 of/PRF Tom/NP0 ./PUN (BNC CB8)
Note that each corpus has its own set of POS tags (called a tagset), i.e., its own theory of word classes. In some cases, this is merely a matter of labels. For example, all tagsets have the word class “uninflected adjective”, but it is labeled JJ in BROWN and FLOB and AJ0 in the BNC; all corpora seem to recognize the word-class “infinitive marker” (with only one member, to), but it is labeled TO in BROWN and FLOB, and TO0 in the BNC; all corpora seem to make a difference between auxiliaries like be and do and other verbs, but the label for do is DO in BROWN and LOB, VAD... in FROWN and VD... in the BNC. The ellipsis in these tags indicates that additional letters may follow to distinguish subcategories, such as tense. Again, the corpora seem to recognize the same subcategories: for example, third person forms are signaled by a Z in BROWN and the BNC.
In other cases, the categories themselves differ. For example, in BROWN, all prepositions are labeled IN, while the BNC distinguishes of from other prepositions by labeling the former PRF and the latter PRP; FLOB has a special tag for the preposition for, IF; LOB labels all coordinating conjunctions CC, FLOB has a special tag for BUT, CCB. More drastically, LOB and FLOB treat some sequences of orthographic words as multi-word tokens belonging to a single word class: in front of is treated as a preposition in LOB and FLOB, indicated by labeling all three words IN (LOB) and II (FLOB), with an additional indication that they are part of a sequence: LOB attaches straight double quotes to the second and third word, FLOB adds a 3 to indicate that they are part of a three word sequence and then a number indicating their position in the sequence. Such tag sequences, called ditto tags make sense only if you believe that the individual parts in a multi-word expression lose their independent word-class membership. Even then, we have to check very carefully, which particular multi-word sequences are treated like this and decide whether we agree. The makers of BROWN and the BNC obviously had a more traditional view of word classes, simply treating in front of as a sequence of a preposition, a noun, and another preposition (BROWN) or specifically the subcategory of (BNC).
Ditto tags are a way of tokenizing the corpus at orthographic word boundaries while allowing words to span more than one token. But tokenization itself also differs across corpora. For example, BROWN tokenizes only at orthographic word boundaries (white space or punctuation), while the other three corpora also tokenize at clitic boundaries. They all treat the n’t in words like don't, doesn't, etc. as separate tokens, labeling it XNOT (LOB), XX (FLOB) and XX0 (BNC), while BROWN simply indicates that a word contains this clitic by attaching an asterisk to the end of the POS tag (other clitics, like ‘ll, ’s, etc. are treated similarly).
It is clear, then, that tokenization and part-of-speech tagging are not inherent in the text itself, but are the result of decisions by the corpus makers. But in what sense can these decisions be said to constitute operational definitions? There are two different answers to this question. The first answer is that the theories of tokenization and word classes are (usually) explicitly described in the corpus manual itself or in a guide as to how to apply the tag set. A good example of the latter is Santorini (1990), the most-widely cited tagging guideline for the PENN tagset developed for the PENN treebank but now widely used.
As an example, consider the instructions for the POS tags DT and JJ, beginning with the former:
Determiner – DT This category includes the articles a(n), every, no and the, the indefinite determiners another, any and some, each, either (as in either way), neither (as in neither decision), that, these, this and those, and instances of all and both when they do not precede a determiner or possessive pronoun (as in all roads or both times). (Instances of all or both that do precede a determiner or possessive pronoun are tagged as predeterminers (PDT).) Since any noun phrase can contain at most one determiner, the fact that such can occur together with a determiner (as in the only such case) means that it should be tagged as an adjective (JJ), unless it precedes a determiner, as in such a good time, in which case it is a predeterminer (PDT). (Santorini 1990: 2)
The instructions rely to some extent on undefined categories (such as article, indefinite determiner, etc.). In the case of a closed class like “determiners”, they get around the need to define them by listing their members. In the case of open-class items like “adjectives”, this is not possible, so it is assumed that the annotator knows what the corpus makers mean and the instruction only lists two special cases that might cause confusion:
Adjective – JJ Hyphenated compounds that are used as modifiers are tagged as adjectives (JJ).
EXAMPLES: happy-go-lucky/JJ one-of-a-kind/JJ run-of-the-mill/JJ
Ordinal numbers are tagged as adjectives (JJ), as are compounds of the form n-th X-est, like fourth-largest. (Santorini 1990: 1)
Note that special cases are also listed in the definition of DT, which contains a discussion of grammatical contexts under which the words listed at the beginning of the definition should instead be tagged as predeterminers (PDT) or adjectives (JJ). There is also an entire section in the tagging guidelines that deals with special, exceptional or generally unclear cases, as an example, consider the passage distinguishing uses of certain words as conjunctions (CC) and determiners (DT):
CC or DT When they are the first members of the double conjunctions both ... and, either ... or and neither ... nor, both, either and neither are tagged as coordinating conjunctions (CC), not as determiners (DT).
EXAMPLES: Either/DT child could sing.
But:
Either/CC a boy could sing or/CC a girl could dance.
Either/CC a boy or/CC a girl could sing.
Either/CC a boy or/CC girl could sing.
Be aware that either or neither can sometimes function as determiners (DT) even in the presence of or or nor. EXAMPLE: Either/DT boy or/CC girl could sing. (Santorini 1990: 7)
The mixture of reliance on generally accepted terminology, word lists and illustrations is typical of tagging guidelines (and, as we saw in Section 3.2, of annotation schemes in general). Nevertheless, such tagging guidelines can probably be applied with a relatively high degree of interrater reliability (although I am not aware of a study testing this), but they require considerable skill and experience (try to annotate a passage from your favorite novel or a short newspaper article to see how quickly you run into problems that require some very deep thinking).
However, POS tagging is not usually done by skilled, experienced annotators, bringing us to the second, completely different way in which POS tags are based on operational definitions. The usual way in which corpora are annotated for parts of speech is by processing them using a specialized software application called tagger (a good example is the Tree Tagger (Schmid 1994), which can be downloaded, studied and used relatively freely).
Put simply, these taggers work as follows: For each word, they take into account the probabilities with which the word is tagged as A, B, C, etc., and the probability that a word tagged as A, B, C should occur at this point given the tag assigned to the preceding word. The tagger essentially multiplies both probabilities and then chooses the tag with the highest joint probability. As an example, consider the word cost in (20b), the beginning of which I repeat here:
(21) none/PN of/IN these/DTS wines/NNS should/MD cost/VB much/RB over/RB 8/CD s/NNU per/IN bottle/NN
The wordform cost has a probability of 0.73 (73 percent) of representing a noun and a probability of 0.27 (27 percent) of representing a verb. If the tagger simply went by these probabilities, it would assign the tag NN. However, the probability that modal verb is followed by a noun is 0.01 (1 percent), while the probability that it is followed by a verb is 0.8 (80 percent). The tagger now multiplies the probabilities for noun (0.73 × 0.01 = 0.0072) and for verb (0.27 × 0.8 = 0.216). Since the latter is much higher, the tagger will tag the word (correctly, in this case, as a verb).
But how does the tagger know these probabilities? It has to “learn” them from a corpus that has been annotated by hand by skilled, experienced annotators based on a reliable, valid annotation scheme. Obviously, the larger this corpus, the more accurate the probabilities, the more likely that the tagger will be correct. I will return to this point presently, but first, note that in corpora which have been POS tagged automatically, the tagger itself and the probabilities it uses are the operational definition. In terms of reliability, this is a good thing: If we apply the same tagger to the same text several times, it will give us the same result every time.
In terms of validity, this is a bad thing in two ways: first, because the tagger assigns tags based on learned probabilities rather than definitions. This is likely to work better in some situations than in others, which means that incorrectly assigned tags will not be distributed randomly across parts of speech. For example, the is unlikely to be tagged incorrectly, as it is always a determiner, but that is more likely to be tagged incorrectly, as it is a conjunction about two thirds of the time and a determiner about one third of the time. Likewise, horse is unlikely to be tagged incorrectly as it is a noun 99 percent of the time, but riding is more likely to be tagged incorrectly, as it is a noun about 15 percent of the time and a verb about 85 percent of the time. A sequence like the horse is almost certain to be tagged correctly, but a sequence like that riding much less so. What is worse, in the latter case, whether riding will be tagged correctly depends on whether that has been tagged correctly. If that has been tagged as a determiner, riding will be (correctly) tagged as a noun, as verbs never follow determiners and the joint probability that it is a verb will be zero. In contrast, if that has been tagged as a conjunction, the tagger will tag riding as a verb: conjunctions are followed by verbs with a probability of 0.16 and by nouns with a probability of 0.11, and so the joint probability that it is a verb (0.16 × 0.85 = 0.136) is higher than the joint probability that it is a noun (0.11 × 0.67 = 0.0165). This will not always be the right decision, as (22) shows:
(22) [W]e did like to make it quite clear during our er discussions that riding of horses on the highway is a matter for the TVP (BNC JS8)
In short, some classes of word forms (like ing-forms of verbs) are more difficult to tag correctly than others, so incorrectly assigned tags will cluster around such cases. This can lead to considerable distortions in the tagging of specific words and grammatical constructions. For example, in the BNC, the word form regard is systematically tagged incorrectly as a verb in the complex prepositions with regard to and in regard to, but is correctly tagged as a noun in most instances of the phrase in high regard. In other words, particular linguistic phenomena will be severely misrepresented in the results of corpus queries based on automatically assigned tags or parse trees.
Sometimes the probabilities of two possible tags are very close. In these cases, some taggers will stoically assign the more probable tag even if the difference in probabilities is small. Other taggers will assign so-called ambiguity or portmanteau tags, as in the following example from the BNC:
(23) Ford/NP0-NN1 faces/NN2-VVZ strike/VVB-NN1 over/AVP-PRP pay/NN1-VVB deal/NN1-VVB ./PUN (BNC AAC)
First, such cases must obviously be kept in mind when constructing queries: the query ⟨ VBB ⟩ will miss the word strike in this sentence (as will the query ⟨ NN1 ⟩). In order to find words with ambiguity tags, we have to indicate that the ag we are interested in may be preceded or followed by another tag (one such way is provided by regular expressions, see Section 4.1 below). Second, such cases demonstrate vividly why the two operational definitions of parts of speech – by tagging guide line and by tagger – are fundamentally different: no human annotator, even one with a very sketchy tagging guideline, would produce the annotation in (23). On the other hand, it is simply not feasible to annotate a 100-million-word corpus using human annotators (though advances in crowdsourcing technology may change this), so we are stuck with a choice between using a tagger or having no POS annotation at all.
Existing taggers tend to have an accuracy of around 95 to 97 percent. For example, it has been estimated (Leech et al. 1994) that 1.5 percent of all words in the BNC are tagged incorrectly. In a further 3.5 percent, the automatic tagger was not able to make a decision, assigning ambiguity tags (as shown in (23) above).
This leaves 95 percent of the words in the corpus tagged correctly and unambiguously. As impressive as this sounds at first, a closer look reveals two problems. First, an accuracy of 95 percent means that roughly one word in 20 is tagged incorrectly. Assuming a mean sentence length of 20 words (actual estimates range from 16 to 22), every sentence contains on average one incorrectly or ambiguously tagged word. Second, as pointed out above, some (classes of) word forms are more difficult to tag correctly, so the five percent mistagged or ambiguously tagged words will not be spread randomly through the data.
3.2.2.2 Length
There is a wide range of phenomena that has been claimed and/or shown to be related to the weight of linguistic units (syllables, words or phrases) – word-order phenomena following the principle “light before heavy”, such as the dative alternation (Thompson & Koide 1987), particle placement (Chen 1986),s-possessive (or “genitive”) and of -construction (Deane 1987) and frozen binominals (Sobkowiak 1993), to name just a few. In the context of such claims, weight is sometimes understood to refer to structural complexity, sometimes to length, and sometimes to both. Since complexity is often difficult to define, it is, in fact, frequently operationalized in terms of length, but let us first look at the difficulty of defining length in its own right and briefly return to complexity below.
Let us begin with words. Clearly, words differ in length – everyone would agree that the word stun is shorter than the word flabbergast. There are a number of ways in which we could operationalize WORD LENGTH, all of which would allow us to confirm this difference in length:
- as “number of letters” (cf., e.g., Wulff 2003), in which case flabbergast has a length of 11 and stun has a length of 4;
- as “number of phonemes” (cf., e.g., Sobkowiak 1993), in which case flabbergast has a length of 9 (BrE /ˈflæbəɡɑːst/ and AmE /flæbɚɡæst/), and stun has a length of 4 (BrE and AmE /stʌn/);
- as “number of syllables” (cf., e.g., Sobkowiak 1993, Stefanowitsch 2003), in which case flabbergast has a length of 3 and stun has a length of 1.
While all three operationalizations give us comparable results in the case of these two words, they will diverge in other cases. Take disconcert, which has the same length as flabbergast when measured in terms of phonemes (it has nine; BrE /dɪskənsɜt/ and AmE /dɪskənsɝːt/) or syllables (three), but it is shorter when measured in terms of letters (ten). Or take shock, which has the same length as stun when measured in syllables (one), but is longer when measured in letters (5 vs. 4) and shorter when measured in phonemes (3 vs. 4; BrE /ʃɑk/ and AmE /ʃɑːk/). Or take amaze, which has the same length as shock in terms of letters (five), but is longer in terms of phonemes (4 or 5, depending on how we analyze the diphthong in /əmeɪz/) and syllables (2 vs. 1).2
Clearly, none of these three definitions is “correct” – they simply measure different ways in which a word may have (phonological or graphemic) length. Which one to use depends on a number of factors, including first, what aspect of word length is relevant in the context of a particular research project (this is the question of validity), and second, to what extent are they practical to apply (this is the question of reliability). The question of reliability is a simple one: “number of letters” is the most reliably measurable factor assuming that we are dealing with written language or with spoken language transcribed using standard orthography; “number of phonemes” can be measured less reliably, as it requires that data be transcribed phonemically (which leaves more room for interpretation than orthography) or, in the case of written data, converted from an orthographic to a phonemic representation (which requires assumptions about which the language variety and level of formality the writer in question would have used if they had been speaking the text); “number of syllables” also requires such assumptions.
The question of validity is less easy to answer: if we are dealing with language that was produced in the written medium, “number of letters” may seem like a valid measure, but writers may be “speaking internally” as they write, in which case orthographic length would play a marginal role in stylistic and/or processing-based choices. Whether phonemic length or syllabic length are the more valid measure may depend on particular research questions (if rhythmic considerations are potentially relevant, syllables are the more valid measure), but also on particular languages; for example, Cutler et al. (1986) have shown that speakers of French (and other so-called syllable-timed languages) process words syllabically, in which case phonemic length would never play a role, while English (and other stress-timed languages) process them phonemically (in which case it depends on the phenomenon, which of the measures are more valid).3
Finally, note that of course phonemic and/or syllabic length correlate with orthographic length to some extent (in languages with phonemic and syllabic scripts), so we might use the easily and reliably measured orthographic length as an operational definition of phonemic and/or syllabic length and assume that mismatches will be infrequent enough to be lost in the statistical noise (cf. Wulff 2003).
When we want to measure the length of linguistic units above word level, e.g. phrases, we can choose all of the above methods, but additionally or instead we can (and more typically do) count the number of words and/or constituents (cf. e.g. Gries (2003a) for a comparison of syllables and words as a measure of length). Here, we have to decide whether to count orthographic words (which is very reliable but may or may not be valid), or phonological words (which is less reliable, as it depends on our theory of what constitutes a phonological word).
As mentioned at the beginning of this subsection, weight is sometimes understood to refer to structural complexity rather than length. The question how to measure structural complexity has been addressed in some detail in the case of phrases, where it has been suggested that COMPLEXITY could be operationalized as “number of nodes” in the tree diagram modeling the structure of the phrase (cf. Wasow & Arnold 2003). Such a definition has a high validity, as “number of nodes” directly corresponds to a central aspect of what it means for a phrase to be syntactically complex, but as tree diagrams are highly theory-dependent, the reliability across linguistic frameworks is low.
Structural complexity can also be operationalized at various levels for words. The number of nodes could be counted in a phonological description of a word. For example, two words with the same number of syllables may differ in the complexity of those syllables: amaze and astound both have two syllables, but the second syllable of amaze follows a simple CVC pattern, while that of astound has the much more complex CCVCC pattern. The number of nodes could also be counted in the morphological structure of a word. In this case, all of the words mentioned above would have a length of one, except disconcert, which has a length of 2 (dis + concert).
Due to the practical and theoretical difficulties of defining and measuring complexity, the vast majority of corpus-based studies operationalize Weight in terms of some measure of Word Length even if they theoretically conceptualize it in terms of complexity. Since complexity and length correlate to some extent, this is a justifiable simplification in most cases. In any case, it is a good example of how a phenomenon and its operational definition may be more or less closely related.
3.2.2.3 Discourse status
The notion of “topical”, “old”, or “given” information plays an important role in many areas of grammar, such as pronominal reference, voice, and constituent order in general. Definitions of this construct vary quite drastically across researchers and frameworks, but there is a simple basis for operational definitions of Topicality in terms of “referential distance”, proposed by Talmy Givón:
(24) Referential Distance [...] assesses the gap between the previous occurrence in the discourse of a referent/topic and its current occurrence in a clause, where it is marked by a particular grammatical coding device. The gap is thus expressed in terms of number of clauses to the left. The minimal value that can be assigned is thus 1 clause [...] (Givón 1983: 13)
This is not quite an operational definition yet, as it cannot be applied reliably without a specification of the notions clause and coding device. Both notions are to some extent theory-dependent, and even within a particular theory they have to be defined in the context of the above definition of referential distance in a way that makes them identifiable.
With respect to coding devices, it has to be specified whether only overt references (by lexical nouns, proper names and pronouns) are counted, or whether covert references (by structural and/or semantic positions in the clause that are not phonologically realized) are included, and if so, which kinds of covert references. With respect to clauses, it has to be specified what counts as a clause, and it has to be specified how complex clauses are to be counted.
A concrete example may demonstrate the complexity of these decisions. Let us assume that we are interested in determining the referential distance of the pronouns in the following example, all of which refer to the person named Joan (verbs and other elements potentially forming the core of a clause have been indexed with numbers for ease of reference in the subsequent discussion):
(25) Joan, though Anne’s junior1 by a year and not yet fully accustomed2 to the ways of the nobility, was3 by far the more worldly-wise of the two. She watched4 , listened5 , learned6 and assessed7 , speaking8 only when spoken9 to in general – whilst all the while making10 her plans and looking11 to the future... Enchanted12 at first by her good fortune in becoming13 Anne Mowbray’s companion, grateful14 for the benefits showered15 upon her, Joan rapidly became16 accustomed to her new role. (BNC CCD)
Let us assume the traditional definition of a clause as a finite verb and its dependents and let us assume that only overt references are counted. If we apply these definitions very narrowly, we would put the referential distance between the initial mention of Joan and the first pronominal reference at 1, as Joan is a dependent of was in clause (253 ) and there are no other finite verbs between this mention and the pronoun she. A broader definition of clause along the lines of “a unit expressing a complete proposition” however, might include the structures (251 ) (though Anne’s junior by a year) and (252 ) (not yet fully accustomed to the ways of the nobility) in which case the referential distance would be 3 (a similar problem is posed by the potential clauses (2512) and (2514), which do not contain finite verbs but do express complete propositions). Note that if we also count the NP the two as including reference to the person named Joan, the distance to she would be 1, regardless of how the clauses are counted.
In fact, the structures (251 ) and (252 ) pose an additional problem: they are dependent clauses whose logical subject, although it is not expressed, is clearly coreferential with Joan. It depends on our theory whether these covert logical subjects are treated as elements of grammatical and/or semantic structure; if they are, we would have to include them in the count.
The differences that decisions about covert mentions can make are even more obvious when calculating the referential distance of the second pronoun, her (in her plans). Again, assuming that every finite verb and its dependents form a clause the distance between her and the previous use she is six clauses (254 to 259 ). However, in all six clauses, the logical subject is also Joan. If we include these as mentions, the referential distance is 1 again (her good fortune is part of the clause (2512) and the previous mention would be the covert reference by the logical subject of clause (2511)).
Finally, note that I have assumed a very flat, sequential understanding of “number of clauses” counting every finite verb separately. However, one could argue that the sequence She watched4 , listened5 , learned6 , and assessed7 is actually a single clause with four coordinated verb phrases sharing the subject she, that speaking8 only when spoken9 to in general is a single clause consisting of a matrix clause and an embedded adverbial clause, and that this clause itself is dependent on the clause with the four verb phrases. Thus, the sequence from (254 ) to (259 ) can be seen as consisting of six, two or even just one clause, depending on how we decide to count clauses in the context of referential distance.
Obviously, there is no “right” or “wrong” way to count clauses; what matters is that we specify a way of counting clauses that can be reliably applied and that is valid with respect to what we are trying to measure. With respect to reliability, obviously the simpler our specification, the better (simply counting every verb, whether finite or not, might be a good compromise between the two definitions mentioned above). With respect to validity, things are more complicated: referential distance is meant to measure the degree of activation of a referent, and different assumptions about the hierarchical structure of the clauses in question are going to have an impact on our assumptions concerning the activation of the entities referred to by them.
Since specifying what counts as a clause and what does not is fairly complex, it might be worth thinking about more objective, less theory-dependent measures of distance, such as the number of (orthographic) words between two mentions (I am not aware of studies that do this, but finding out to what extent the results correlate with clause-based measures of various kinds seems worthwhile).
For practical as well as for theoretical reasons, it is plausible to introduce a cutoff point for the number of clauses we search for a previous mention of a referent: practically, it will become too time consuming to search beyond a certain point, theoretically, it is arguable to what extent a distant previous occurrence of a referent contributes to the current information status. Givón (1983) originally set this cut-off point at 20 clauses, but there are also studies setting it at ten or even at three clauses. Clearly, there is no “correct” number of clauses, but there is empirical evidence that the relevant distinctions are those between a referential distance of 1, between 2 and 3, and > 3 (cf. Givón 1992).
Note that, as an operational definition of “topicality” or “givenness”, it will miss a range of referents that are “topical” or “given”. For example, there are referents that are present in the minds of speakers because they are physically present in the speech situation, or because they constitute salient shared knowledge for them, or because they talked about them at a previous occasion, or because they were mentioned prior to the cut-off point. Such referents may already be “given” at the point that they are first mentioned in the discourse.
Conversely, the definition may wrongly classify referents as discourse-active. For example, in conversational data an entity may be referred to by one speaker but be missed or misunderstood by the hearer, in which case it will not constitute given information to the hearer (Givón originally intended the measure for narrative data only, where this problem will not occur).
Both WORD LENGTH and DISCOURSE STATUS are phenomena that can be defined in relatively objective, quantifiable terms – not quite as objectively as physical HARDNESS, perhaps, but with a comparable degree of rigor. Like Hardness measures, they do not access reality directly and are dependent on a number of assumptions and decisions, but providing that these are stated sufficiently explicitly, they can be applied almost automatically. While WORD LENGTH and DISCOURSE STATUS are not the only such phenomena, they are not typical either. Most phenomena that are of interest to linguists (and thus, to corpus linguists) require operational definitions that are more heavily dependent on interpretation. Let us look at two such phenomena, WORD SENSE and ANIMACY.
3.2.2.4 Word senses
Although we often pretend that corpora contain words, they actually contain graphemic strings. Sometimes, such a string is in a relatively unique relationship with a particular word. For example, sidewalk is normally spelled as an uninterrupted sequence of the character S or s followed by the characters i, d, e, w, a, l and k, or as an uninterrupted sequence of the characters S, I, D, E, W, A, L and K, so (assuming that the corpus does not contain hyphens inserted at the end of a line when breaking the word across lines), there are just three orthographic forms; also, the word always has the same meaning. This is not the case for pavement, which, as we saw, has several meanings that (while clearly etymologically related), must be distinguished.
In these cases, the most common operationalization strategy found in corpus linguistics is reference to a dictionary or lexical database. In other words, the researcher will go through the concordance and assign every instance of the orthographic string in question to one word-sense category posited in the corresponding lexical entry. A resource frequently used in such cases is the WordNet database (cf. Fellbaum 1998, see also Study Notes). This is a sort of electronic dictionary that includes not just definitions of different word senses but also information about lexical relationships, etc.; but let us focus on the word senses. For pavement, the entry looks like this:
(26) a. S: (n) pavement#1, paving#2 (the paved surface of a thoroughfare)
b. S: (n) paving#1, pavement#2, paving material#1 (material used to pave an area)
c. S: (n) sidewalk#1, pavement#3 (walk consisting of a paved area for pedestrians; usually beside a street or roadway)
There are three senses of pavement, as shown by the numbers attached, and in each case there are synonyms. Of course, in order to turn this into an operational definition, we need to specify a procedure that allows us to assign the hits in our corpus to these categories. For example, we could try to replace the word pavement by a unique synonym and see whether this changes the meaning. But even this, as we saw in Section 3.1.2 above, may be quite difficult.
There is an additional problem: We are relying on someone else’s decisions about which uses of a word constitute different senses. In the case of pavement, this is fairly uncontroversial, but consider the entry for the noun bank:
(27) a. bank#1 (sloping land (especially the slope beside a body of water))
b. bank#2, depository financial institution#1, bank#2, banking concern#1, banking company#1 (a financial institution that accepts deposits and channels the money into lending activities)
c. bank#3 (a long ridge or pile)
d. bank#4 (an arrangement of similar objects in a row or in tiers)
e. bank#5 (a supply or stock held in reserve for future use (especially in emergencies))
f. bank#6 (the funds held by a gambling house or the dealer in some gambling games)
g. bank#7, cant#2, camber#2 (a slope in the turn of a road or track; the outside is higher than the inside in order to reduce the effects of centrifugal force)
h. savings bank#2, coin bank#1, money box#1, bank#8 (a container (usually with a slot in the top) for keeping money at home)
i. bank#9, bank building#1 (a building in which the business of banking transacted)
j. bank#10 (a flight maneuver; aircraft tips laterally about its longitudinal axis (especially in turning))
While everyone will presumably agree that (27a) and (27b) are separate senses (or even separate words, i.e. homonyms), it is less clear whether everyone would distinguish (27b) from (27i) and/or (27f); or (27e) and (27f), or even (27a) and (27g). In these cases, one could argue that we are just dealing with contextual variants of a single underlying meaning.
Thus, we have the choice of coming up with our own set of senses (which has the advantage that it will fit more precisely into the general theoretical framework we are working in and that we might find it easier to apply), or we can stick with an established set of senses such as that proposed by WordNet, which has the advantage that it is maximally transparent to other researchers and that we cannot subconsciously make it fit our own preconceptions, thus distorting our results in the direction of our hypothesis. In either case, we must make the set of senses and the criteria for applying them transparent, and in either case we are dealing with an operational definition that does not correspond directly with reality (if only because word senses tend to form a continuum rather than a set of discrete categories in actual language use).
3.2.2.5 Animacy
The animacy of the referents of noun phrases plays a role in a range of grammatical processes in many languages. In English, for example, it has been argued (and shown) to be involved in the grammatical alternations already discussed above, in other languages it is involved in grammatical gender, in alignment systems, etc.
The simplest distinction in the domain of ANIMACY would be the following:
(28) ANIMATE vs. INANIMATE
Dictionary definitions typically treat animate as a rough synonym of alive (OALD and CALD define it as “having life”), and inanimate as a rough synonym of not alive, normally in the sense of not being capable of having life, like, for example, a rock (“having none of the characteristics of life that an animal or plant has”, CALD, see also OALD), but sometimes additionally in the sense of being no longer alive (“dead or appearing to be dead”, OALD).
The basic distinction in (28) looks simple, so that any competent speaker of a language should be able to categorize the referents of nouns in a text accordingly. On second thought, however, it is more complex than it seems. For example, what about dead bodies or carcasses? The fact that dictionaries disagree as to whether these are inanimate shows that this is not a straightforward question that calls for a decision before the nouns in a given corpus could be categorized reliably.
Let us assume for the moment that animate is defined as “potentially having life” and thus includes dead bodies and carcasses. This does not solve all problems: For example, how should body parts, organs or individual cells be categorized? They “have life” in the sense that they are part of something alive, but they are not, in themselves, living beings. In fact, in order to count as an animate being in a communicatively relevant sense, an entity has to display some degree of intentional agency. This raises the question of whether, for example, plants, jellyfish, bacteria, viruses or prions should be categorized as animate.
Sometimes, the dimension of intentionality/agency is implicitly recognized as playing a crucial role, leading to a three-way categorization such as that in (29):
(29) HUMAN VS. OTHER ANIMATE VS. INANIMATE
If ANIMACY is treated as a matter of degree, we might want to introduce further distinctions in the domain of animates, such as HIGHER ANIMALS, LOWER ANIMALS, PLANTS, MICRO-ORGANISMS. However, the distinction between HUMANS and OTHER ANIMATES introduces additional problems. For example, how should we categorize animals that are linguistically represented as quasi-human, like the bonobo Kanzi, or a dog or a cat that is treated by their owner as though it has human intelligence? If we categorize them as OTHER ANIMATE, what about fictional talking animals like the Big Bad Wolf and the Three Little Pigs? And what about fully fictional entities, such as gods, ghosts, dwarves, dragons or unicorns? Are they, respectively, humans and animals, even though they do not, in fact exist? Clearly, we treat them conceptually as such, so unless we follow an extremely objectivist semantics, they should be categorized accordingly – but this is not something we can simply assume implicitly.
A slightly different problem is posed by robots (fictional ones that have quasihuman or quasi-animal capacities and real ones, that do not). Should these be treated as HUMANS/ANIMATE? If so, what about other kinds of “intelligent” machines (again, fictional ones with quasi-human capacities, like HAL 9000 from Arthur C. Clarke’s Space Odyssey series, or real ones without such capacities, like the laptop on which I am writing this book)? And what about organizations (when they are metonymically treated as agents, and when they are not)? We might want to categorize robots, machines and organizations as human/animate in contexts where they are treated as having human or animal intelligence and agency, and as inanimate where they are not. In other words, our categorization of a referent may change depending on context.
Sometimes studies involving animacy introduce additional categories in the INANIMATE domain. One distinction that is often made is that between concrete and abstract, yielding the four-way categorization in (30):
(30) HUMAN VS. ANIMATE VS. CONCRETE INANIMATE VS. ABSTRACT INANIMATE
The distinction between concrete and abstract raises the practical issue where to draw the line (for example, is electricity concrete?). It also raises a deeper issue that we will return to: are we still dealing with a single dimension? Are abstract inanimate entities (say, marriage or Wednesday) really less “animate” than concrete entities like a wedding ring or a calendar? And are animate and abstract incompatible, or would it not make sense to treat the referents of words like god, demon, unicorn, etc. as abstract animate?
3.2.2.6 Interim summary
We have seen that operational definitions in corpus linguistics may differ substantially in terms of their objectivity. Some operational definitions, like those for length and discourse status, are almost comparable to physical measures like Vickers Hardness in terms of objectivity and quantitativeness. Others, like those for word senses or animacy are more like the definitions in the DSM or the ICD in that they leave room for interpretation, and thus for subjective choices, no matter how precise the instructions for the identification of individual categories are. Unfortunately, the latter type of operational definition is more common in linguistics (and the social sciences in general), but there are procedures to deal with the problem of subjectiveness at least to some extent. We will return to these procedures in detail in the next chapter.
2 Note that I have limited the discussion here to definitions of length that make sense in the domain of traditional linguistic corpora; there are other definitions, such as phonetic length (time it took to pronounce an instance of the word in a specific situation), or mean phonetic length (time it takes to pronounce the word on average). For example, the pronunciation samples of the CALD, as measured by playing them in the browser Chrome (Version 32.0.1700.102 for Mac OSX) and recording them using the software Audacity (Version 2.0.3 for Mac OSX) on a MacBook Air with a 1.8 GHz Intel Core i5 processor and running OS X version 10.8.5 and then using Audacity’s timing function, have the following lengths: flabbergast BrE 0.929s, AmE 0.906s and stun BrE 0.534s, AmE 0.482s. The reason I described the hardware and software I used in so much detail is that they are likely to have influenced the measured length in addition to the fact that different speakers will produce words at different lengths on different occasions; thus, calculating meaningful mean pronunciation lengths would be a very time- and resource-intensive procedure even if we decided that it was the most valid measure of Word Length in the context of a particular research project. I am not aware of any corpus-linguistic study that has used this definition of word length; however, there are versions of the SWITCHBOARD corpus (a corpus of transcribed telephone conversations) that contain information about phonetic length, and these have been used to study properties of spoken language (e.g. Greenberg et al. 1996; 2003).
3 The difference between these two language types is that in stress-timed languages, the time between two stressed syllables tends to be constant regardless of the number of unstressed syllables in between, while in syllable-timed languages every syllable takes about the same time to pronounce. This suggests an additional possibility for measuring length in stress-timed languages, namely the number of stressed syllables. Again, I am not aware of any study that has discussed the operationalization of word length at this level of detail.


