18.6: Chapter 10- Computer Models and Learning in Artificial Neural Networks
- Page ID
- 139941
This page is a draft and under active development. Please forward any questions, comments, and/or feedback to the ASCCC OERI (oeri@asccc.org).
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Explain Hebb's rule and how it is applied in connectionist networks
- Describe connection weights and how their modification by inputs to them create "learning" in a connectionist network
- Describe the structure of a simple three-layer network
- Explain what is meant by "coarse coding" and give an example
- Explain Hebb's concept of "cell assemblies"
- Discuss how the graded potentials (EPSPs and IPSPs) in biological neurons undergo a nonlinear transformation during neural communication permitting emergent properties
Overview
Artificial neural networks, or connectionist networks, are computer generated models using principles of computing based loosely on how biological neurons and biological neuron networks operate. Processing units in connectionist networks are frequently arranged in interconnected layers. The connections between processing units in connectionist networks are modifiable and can therefore become stronger or weaker, similar to the way that synapses in the brain are presumed to be modified in strength by learning and experience. Cognitive processes can be studied using artificial neural networks providing insights into how biological brains may code and process information.
Hebbian Synapses, Modification of Connection Weights, and Learning in Artificial Neural Networks
Hebbian Learning, also known as Hebb's Rule or Cell Assembly Theory, attempts to connect the psychological and neurological underpinnings of learning. As discussed in an earlier section of this chapter, the basis of Hebb's theory is when our brains learn something new, neurons are activated and connected with other neurons, forming a neural network or cell assembly (a group of synaptically connected neurons) which can represent cognitive structures such as perceptions, concepts, thinking, or memories. How large groups of neurons generate such cognitive structures and processes is unknown. However, in recent years, researchers from neuroscience and computer science have made advances in our understanding of how neurons work together by using computer modeling of brain activity. Not only has computer modeling of brain processes provided new insights about brain mechanisms in learning, memory, and other cognitive functions, but artificial intelligence (AI) research also has powerful practical applications in many areas of human endeavor.
The influence of Hebb's book, The Organization of Behavior (1949), has spread beyond psychology and neuroscience to the field of artificial intelligence research using artificial neural networks. An artificial neural network is a computer simulation of a "brain-like" system of interconnected processing units, similar to neurons. These processing units, sometimes referred to as "neurodes," mimic many of the properties of biological neurons. For example, "neurodes" in artificial neural networks have connections among them similar to the synapses in biological brains. Just like the strengths of conductivity of synapses between biological neurons can be modified by experience (i.e. learning), the synaptic "weights" at connections between "neurodes" can also be modified by inputs to the system, permitting artificial neural networks to learn. The basic idea is that changes in "connection weights" by inputs to an artifical network are analogous to the changes in synaptic strengths between neurons in the brain during learning. Recall from a prior section that experience can strengthen the associative link between neurons when the activity in those neurons occurs together (i.e. Hebb's Rule). In artificial neural networks, also called connectionist networks, when connection weights between processing units are altered by inputs, the output of the network changes--the artificial neural network learns.
Like biological synapses, the connections between processing units in an artificial neural network can be inhibitory as well as excitatory. "The synaptic weight in an artificial neural network is a number that defines the nature and strength of the connection. For example, inhibitory connections have negative weights, and excitatory connections have positive weights. Strong connections have strong weights. The signal sent by one processor to another is a number that is transmitted through the weighted connection or "synapse." The "synaptic" connection and its corresponding "weight" serves as a communication channel between processing units (neurodes) that amplifies or diminishes signals being sent through it; the "synaptic" connection amplifies or diminishes the signal because these signals are multiplied by the weight (either positive or negative and of varying magnitude) associated with the "synaptic" connection. Strong connections, either positive or negative, have large (in terms of absolute value disregarding sign) weights and large effects on the signal, while weak connections have near-zero weights" (Libretext, Mind, Body, World: Foundations of Cognitive Science (Dawson), 4.2, Nature vs Nurture). Changes in synaptic "weights" change the output of the neural network constituting learning by the network. Notice the clear similarity to Hebb's conception of learning in biological brains.
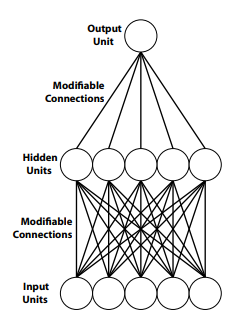
Figure \(\PageIndex{1}\): A multilayer neural network with one layer of hidden units between input and output units. (Image from Libretext, Mind, Body, World: Foundations of Cognitive Science (Dawson), 4.5, The Connectionist Sandwich; https://socialsci.libretexts.org/Boo...onist_Sandwich)
Additional hidden layers increase the complexity of the processing that a network can perform. Artificial neural networks with multiple layers have been shown to be capable of quite complex representations and sophisticated learning and problem-solving. This approach to modeling learning, memory, and cognition is known as "connectionism" (see Matter and Consciousness by Paul Churchland, MIT Press, 2013, for an excellent and very readable introduction to the field) and is the basis for much of the research in the growing field of artificial intelligence, including voice recognition and machine vision.
Recall that Hebb (1949) proposed that if two interconnected neurons are both “on” at the same time, then the synaptic weight between them should be increased. Thus, Hebbian learning is a form of activity-dependent synaptic plasticity where correlated activation of pre- and postsynaptic neurons leads to the strengthening of the connection between the two neurons. "The Hebbian learning rule is one of the earliest and the simplest learning rules for neural networks," "and is based in large part on the dynamics of biological systems. A synapse between two neurons is strengthened when the neurons on either side of the synapse (pre- and post-synaptic) have highly correlated outputs (recall the sections of this chapter on LTP). In essence, when an input neuron fires, if it frequently leads to the firing of the output neuron, the synapse is strengthened." Similarly, in an artificial neural network, the "synaptic" weight or strength between units in an artificial neural network "is increased with high correlation between the firing of the pre-synaptic and post-synaptic" units (adapted from Wikibooks, Artificial Neural Networks/Hebbian Learning, https://en.wikibooks.org/wiki/Artifi...bbian_Learning; retrieved 8/13/2021). Artificial neural networks are not hard wired. Instead, they learn from experience to set the values of their connection weights, just as might occur in biological brains when they learn. Changing connection weights within the network, changes the network's output, its "behavior." This is the physical basis of learning in an artificial neural network (a connectionist network) and is analogous to the changes in the brain believed to be the physical basis of learning in animals and humans.
More complex artificial neural networks of several different types using different learning rules or paradigms have been developed, but regardless of the learning rule employed, each uses modification of synaptic weights (synaptic strengths) to modify outputs as learning by the connectionist network proceeds--a fundamentally Hebbian idea.
In some systems, called self-organizing networks, experience shapes connectivity via "unsupervised learning" (Carpenter & Grossberg, 1992). When learning is unsupervised, networks are only provided with input patterns. Networks whose connection weights are modified via unsupervised learning develop sensitivity to statistical regularities in the inputs and organize their output units to reflect these regularities. In this case, the connectionist artificial neural network can discover new patterns in data not previously recognized by humans.
In cognitive science, most networks reported in the literature are not self-organizing and are not structured via unsupervised learning. Instead, they are networks that are instructed to mediate a desired input-output mapping. This is accomplished via supervised learning. In supervised learning, it is assumed that the network has an external "teacher." The network is presented with an input pattern and produces a response to it. The teacher compares the response generated by the network to the desired response, usually by calculating the amount of error associated with each output unit. The "teacher" then provides the error as feedback to the network. A learning rule (such as the delta rule) uses feedback about error to modify connection weights in the network in such a way that the next time this pattern is presented to the network, the amount of error that it produces will be smaller. Technically, this learning paradigm is called "back-propagation of error" and may be analogous to feedback learning in animals and humans learning to reach a goal (think of operant conditioning, specifically operant shaping).
Representation and Processing of Information in Artifical Networks Gives Clues About Representation and Processing in Biological Brains
One of the assumed advantages of connectionist cognitive science (a branch of psychology, neuroscience, and computer science that attempts to use connectionist systems to model human psychological processes) is that it can inspire alternative notions of representation of information in the brain. How do neurons, populations of neurons, and their operations represent perceptions, mental images, memories, concepts, categories, ideas and other cognitive structures? Coarse coding may be one answer.
A coarse code is one in which an individual processing unit is very broadly tuned, sensitive to either a wide range of features or at least to a wide range of values for an individual feature (Churchland & Sejnowski, 1992; Hinton, McClelland, & Rumelhart, 1986). In other words, individual processors are themselves very inaccurate devices for measuring or detecting a feature of the world, such as color. The accurate representation of a feature can become possible, though, by pooling or combining the responses of many such inaccurate detectors, particularly if their perspectives are slightly different (e.g., if they are sensitive to different ranges of features, or if they detect features from different input locations). Here, it is useful to think of auditory receptors, for example, each of which is sensitive to a range of frequencies of sound waves. Precision in discrimination of frequency, experienced as pitch, occurs by patterns of activity in auditory receptor cells ("hair cells" on the basilar membrane inside the cochlea of the inner ear) which are sensitive to overlapping ranges of frequencies (auditory receptive fields). Relative firing rates in a group of auditory receptors with overlapping ranges of sensitivity gives a precise neural coding of each particular frequency.
Another familiar example of coarse coding is provided by the nineteenth century trichromatic theory of color perception (Helmholtz, 1968; Wasserman, 1978). According to this theory, color perception is mediated by three types of retinal cone receptors. One is maximally sensitive to short (blue) wavelengths of light, another is maximally sensitive to medium (green) wavelengths, and the third is maximally sensitive to long (red) wavelengths. Thus none of these types of receptors are capable of representing, by themselves, the rich rainbow of perceptible hues.
However, these receptors are broadly tuned and have overlapping sensitivities. As a result, most light will activate all three channels simultaneously, but to different degrees. Actual colored light does not produce sensations of absolutely pure color; that red fire engine, for instance, even when completely freed from all admixture of white light, still does not excite those nervous fibers which alone are sensitive to impressions of red, but also, to a very slight degree, those which are sensitive to green, and perhaps to a still smaller extent those which are sensitive to violet rays (Helmholtz, 1968, p. 97).
The study of artificial neural networks has provided biological psychologists and cognitive neuroscientists new insights about how the brain might process information in ways that generate perception, learning and memory, and various forms of cognition including visual recognition and neural representation of spatial maps in the brain (one function of the mammalian hippocampus). Even critics of connectionism admit that “the study of connectionist machines has led to a number of striking and unanticipated findings; it’s surprising how much computing can be done with a uniform network of simple interconnected elements” (Fodor & Pylyshyn, 1988, p. 6). Hillis (1988, p. 176) has noted that artificial neural networks allow “for the possibility of constructing intelligence without first understanding it.” As one researcher put it, “The major lesson of neural network research, I believe, has been to thus expand our vision of the ways a physical system like the brain might encode and exploit information and knowledge” (Clark, 1997, p. 58).
The key idea in connectionism is association: different ideas can be linked together, so that if one arises, then the association between them causes the other to arise as well. Note the similarity to Hebb's concept of cell assemblies, formed by associations mediated by changes in synapses, and the association of cell assemblies with one another via the same mechanism. Once again, Hebb's influence is evident in connectionism's artificial neural networks--even the name, connectionism, reflects Hebb's ideas about how cognitive structures and learning and memory are formed in the brain--by changes in connections between neurons. As previously discussed, long-term potentiation (LTP) has been extensively studied by biological psychologists and neuroscientists as a biologically plausible mechanism for the synaptic alterations by experience proposed in Hebb’s theory of learning and memory in biological brains.
While association is a fundamental notion in connectionist models, other notions are required by modern connectionist cognitive science in the effort to model complex properties of the mind. One of these additional ideas is nonlinear processing. If a system is linear, then its whole behavior is exactly equal to the sum of the behaviors of its parts. Emergent properties, however, where the properties of a whole (i.e., a complex idea) are more than the sum of the properties of the parts (for example, a set of associated simpler ideas), require nonlinear processing. Complex cognition, perception, learning and memory may be emergent properties arising from the activities of the brain's neurons and networks. This observation suggests that nonlinear processing is a key feature of how information is represented and processed in the brain. We can see the presence of nonlinear processing at the level of individual neurons.
Neurons demonstrate one powerful type of nonlinear processing involving action potentials. As discussed in chapter 5, the inputs to a neuron are weak electrical signals, called graded potentials (EPSPs and IPSPs; see chapter 5 on Communication within the Nervous System), which stimulate and travel through the dendrites of the receiving neuron. If enough of these weak graded potentials arrive at the neuron’s soma at roughly the same time, then they summate and if their cumulative effect reaches the neuron’s "trigger threshold," a massive depolarization of the membrane of the neuron’s axon, the action potential, occurs. The action potential is a signal of constant intensity that travels along the axon to eventually stimulate some other neuron (see chapter 5). A crucial property of the action potential is that it is an all-or-none phenomenon, representing a nonlinear transformation of the summed graded potentials. The neuron converts continuously varying inputs (EPSPs and IPSPs) into a response that is either on (action potential generated) or off (action potential not generated). This has been called the all-or-none law which states that once an action potential is generated it is always full size, minimizing the possibility that information will be lost as the action potential is conducted along the length of axon. The all-or-none output of neurons is a nonlinear transformation of summed, continuously varying input, and it is the reason that the brain can be described as digital in nature (von Neumann, 1958).
Artificial neural networks have been used to model a dizzying variety of phenomena including animal learning (Enquist & Ghirlanda, 2005), cognitive development (Elman et al., 1996), expert systems (Gallant, 1993), language (Mammone, 1993), pattern recognition and visual perception (Ripley, 1996), and musical cognition (Griffith & Todd, 1999). One neural network even discovered a mathematical proof that human mathematicians had been unable to solve (Churchland, 2013).
Researchers at the University of California at San Diego, and elsewhere in labs around the world, are producing "deep learning" using artificial networks with 5 or more layers that can perform tasks such as facial recognition, object categorization, or speech recognition (see https://cseweb.ucsd.edu//groups/guru/). Although psychologists, PDP researchers, and neuroscientists have a long way to go, modeling of learning and memory, perception, and cognition in artificial (PDP) neural networks has contributed to our understanding of how neurons in the brain's networks may represent, encode and process information during the psychological states that we experience daily, including learning and memory. For example, "The simulation of brain processing by artificial networks suggests that multiple memories can be encoded within a single neural network, by different patterns of synaptic connections. Conversely, a single memory may involve simultaneously activating several different groups of neurons in different parts of the brain" (from The Brain from Top to Bottom; https://thebrain.mcgill.ca/flash/a/a...07_cl_tra.html). As we have seen earlier in this chapter, neural activity from different regions of cerebral cortex converges onto the hippocampus where processing may combine memory traces from different modalities into unified multi-modal memories.
References
Bliss, T. V., & Lømo, T. (1973). Long‐lasting potentiation of synaptic transmission in the dentate area of the anaesthetized rabbit following stimulation of the perforant path. The Journal of physiology, 232(2), 331-356.
Churchland, P. M. (2013). Matter and consciousness. Cambridge, MA. MIT press.
Churchland, P.S. & Sejnowski, T.J. (1992). The Computational Brain. Cambridge, MA. MIT Press.
Clark, A. (1997). Being there: Putting Brain, Body, and World Together Again. Cambridge, MA: MIT Press.
Elman, J. L., Bates, E. A., & Johnson, M. H. (1996). Rethinking innateness: A connectionist perspective on development (Vol. 10). MIT press.
Enquist, M., & Ghirlanda, S. (2005). Neural Networks and Animal Behavior (Vol. 33). Princeton University Press.
Fodor, J. A., & Pylyshyn, Z. W. (1988). Connectionism and cognitive architecture: A critical analysis. Cognition, 28(1-2), 3-71.
Gallant, S. I., & Gallant, S. I. (1993). Neural network learning and expert systems. MIT press.
Griffith, N., Todd, P. M., & Todd, P. M. (Eds.). (1999). Musical networks: Parallel distributed perception and performance. MIT Press.
Hayashi-Takagi, A., Yagishita, S., Nakamura, M., Shirai, F., Wu, Y.I., Loshbaugh, A.L., Kuhlman, B., Hahn, KM., Kasai, H. (2015). Labelling and optical erasure of synaptic memory traces in the motor cortex. Nature 525, 333–338.
Hebb, D.O. (1949). The Organization of Behavior. New York. Wiley.
Helmholtz, H. von, (1968). The recent progress of the theory of vision. Helmholtz on Perception: Its Physiology and Development, Edited by Richard Warren and Roslyn Warren, John Wiley and Sons, New York, London, Sydney, 125.
Henry, F. E., Hockeimer, W., Chen, A., Mysore, S. P., & Sutton, M. A. (2017). Mechanistic target of rapamycin is necessary for changes in dendritic spine morphology associated with long-term potentiation. Molecular Brain, 10 (1), 1-17.
Hillis, W. D. (1988). Intelligence as an emergent behavior; or, the songs of eden. Daedalus, 175-189.
Hinton, G. E., McClelland, J. L., & Rumelhart, D. E. (1986). Parallel distributed processing.
Kandel, E. (1976). Cellular Basis of Behavior. San Francisco. W.H. Freeman and Company.
Kandel, E. R., & Schwartz, J. H. (1982). Molecular biology of learning: Modulation of transmitter release. Science, 218 (4571), 433–443
Kolb, B. & Whishaw, I.Q. (2001). In Introduction to Brain and Behavior. New York. Worth Publishers.
Kozorovitskiy Y, et al. (2005). Experience induces structural and biochemical changes in the adult primate brain. Proc Natl Acad Sci USA.102:17478. [PMC free article] [PubMed]
Mammone, R. J. (Ed.). (1993). Artificial neural networks for speech and vision (Vol. 4). Kluwer Academic Publishers.
Miller, R. R., & Marlin, N. A. (2014). Amnesia following electroconvulsive shock. Functional disorders of memory, 143-178. New York. Psychology Press.
Pinel, P.J. & Barnes, S. (2021). Biopsychology (11th Edition). Boston. Pearson Education.
Renner MJ, & Rosenzweig MR. Enriched and Impoverished Environments: Effects on Brain and Behavior. Springer Verlag; New York: 1987.
Ripley, B.D. (1996) Pattern Recognition and Neural Networks. Cambridge University Press, Cambridge.
Rosenzweig, M. R. (2007). Modification of brain circuits through experience. In Neural Plasticity and Memory: From Genes to Brain Imaging. CRC Press/Taylor & Francis, Boca Raton (FL); 2007. PMID: 21204433.
Von Neumann, J. (1958). The computer and the brain. New Haven, Conn.: Yale University Press.
Wasserman, G. S. (1978). Color vision: An historical introduction. John Wiley & Sons.
Attributions
1. Section 10.9: "Computer Models and Learning in Artificial Neural Networks" by Kenneth A. Koenigshofer, PhD, Chaffey College, licensed CC BY 4.0
2. Parts of the section on "Learning in Artificial Neural Networks," is adapted by Kenneth A. Koenigshofer, PhD, from Libretext, Mind, Body, World: Foundations of Cognitive Science, 4.2, Nature vs Nurture; 4.3, Associations; 4.4 Non-linear transformations; 4.5 The Connectionist Sandwich; 4.19 What is Connectionist Cognitive Science; by Michael R. W. Dawson, LibreTexts; licensed under CC BY-NC-ND.


