18.12: Chapter 14- Problem Solving, Categories and Concepts
- Page ID
- 113223
This page is a draft and under active development. Please forward any questions, comments, and/or feedback to the ASCCC OERI (oeri@asccc.org).
- Define problem types
- Describe problem solving strategies
- Define algorithm and heuristic
- Describe the role of insight in problem solving
- Explain some common roadblocks to effective problem solving
- What is meant by a search problem
- Describe means-ends analysis
- How do analogies and restructuring contribute to problem solving
- Explain how experts solve problems and what gives them an advantage over non-experts
- Describe the brain mechanisms in problem solving
Overview
In this section we examine problem-solving strategies. People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy, usually a set of steps, for solving the problem.
Defining Problems
We begin this module on Problem Solving by giving a short description of what psychologists regard as a problem. Afterwards we are going to present different approaches towards problem solving, starting with gestalt psychologists and ending with modern search strategies connected to artificial intelligence. In addition we will also consider how experts do solve problems and finally we will have a closer look at two topics: The neurophysiological background on the one hand and the question what kind of role can be assigned to evolution regarding problem solving on the other.
The most basic definition is “A problem is any given situation that differs from a desired goal”. This definition is very useful for discussing problem solving in terms of evolutionary adaptation, as it allows to understand every aspect of (human or animal) life as a problem. This includes issues like finding food in harsh winters, remembering where you left your provisions, making decisions about which way to go, repeating and varying all kinds of complex movements by learning, and so on. Though all these problems were of crucial importance during the evolutionary process that created us the way we are, they are by no means solved exclusively by humans. We find a most amazing variety of different solutions for these problems of adaptation in animals as well (just consider, e.g., by which means a bat hunts its prey, compared to a spider).
However, for this module, we will mainly focus on abstract problems that humans may encounter (e.g. playing chess or doing an assignment in college). Furthermore, we will not consider those situations as abstract problems that have an obvious solution: Imagine a college student, let's call him Knut. Knut decides to take a sip of coffee from the mug next to his right hand. He does not even have to think about how to do this. This is not because the situation itself is trivial (a robot capable of recognizing the mug, deciding whether it is full, then grabbing it and moving it to Knut’s mouth would be a highly complex machine) but because in the context of all possible situations it is so trivial that it no longer is a problem our consciousness needs to be bothered with. The problems we will discuss in the following all need some conscious effort, though some seem to be solved without us being able to say how exactly we got to the solution. Still we will find that often the strategies we use to solve these problems are applicable to more basic problems, as well as the more abstract ones such as completing a reading or writing assignment for a college class.
Non-trivial, abstract problems can be divided into two groups:
Well-defined Problems
For many abstract problems it is possible to find an algorithmic solution. We call all those problems well-defined that can be properly formalized, which comes along with the following properties:
- The problem has a clearly defined given state. This might be the line-up of a chess game, a given formula you have to solve, or the set-up of the towers of Hanoi game (which we will discuss later).
- There is a finite set of operators, that is, of rules you may apply to the given state. For the chess game, e.g., these would be the rules that tell you which piece you may move to which position.
- Finally, the problem has a clear goal state: The equations is resolved to x, all discs are moved to the right stack, or the other player is in checkmate.
Not surprisingly, a problem that fulfills these requirements can be implemented algorithmically (also see convergent thinking). Therefore many well-defined problems can be very effectively solved by computers, like playing chess.
Ill-defined Problems
Though many problems can be properly formalized (sometimes only if we accept an enormous complexity) there are still others where this is not the case. Good examples for this are all kinds of tasks that involve creativity, and, generally speaking, all problems for which it is not possible to clearly define a given state and a goal state: Formalizing a problem of the kind “Please paint a beautiful picture” may be impossible. Still this is a problem most people would be able to access in one way or the other, even if the result may be totally different from person to person. And while Knut might judge that picture X is gorgeous, you might completely disagree.
Nevertheless ill-defined problems often involve sub-problems that can be totally well-defined. On the other hand, many every-day problems that seem to be completely well-defined involve a great deal of creativity and many ambiguities. For example, suppose Knut has to read some technical material and then write an essay about it.
If we think of Knut's fairly ill-defined task of writing an essay, he will not be able to complete this task without first understanding the text he has to write about. This step is the first sub-goal Knut has to solve. Interestingly, ill-defined problems often involve subproblems that are well-defined.
Knut’s situation could be explained as a classical example of problem solving: He needs to get from his present state – an unfinished assignment – to a goal state - a completed assignment - and has certain operators to achieve that goal. Both Knut’s short and long term memory are active. He needs his short term memory to integrate what he is reading with the information from earlier passages of the paper. His long term memory helps him remember what he learned in the lectures he took and what he read in other books. And of course Knut’s ability to comprehend language enables him to make sense of the letters printed on the paper and to relate the sentences in a proper way.
Same place, different day. Knut is sitting at his desk again, staring at a blank paper in front of him, while nervously playing with a pen in his right hand. Just a few hours left to hand in his essay and he has not written a word. All of a sudden he smashes his fist on the table and cries out: "I need a plan!
How is a problem represented in the mind?
Generally speaking, problem representations are models of the situation as experienced by the agent. Representing a problem means to analyze it and split it into separate components:
- objects, predicates
- state space
- operators
- selection criteria
Therefore the efficiency of Problem Solving depends on the underlying representations in a person’s mind. Analyzing the problem domain according to different dimensions, i.e., changing from one representation to another, results in arriving at a new understanding of a problem. This is basically what is described as restructuring.
Insight
There are two very different ways of approaching a goal-oriented situation. In one case an organism readily reproduces the response to the given problem from past experience. This is called reproductive thinking.
The second way requires something new and different to achieve the goal, prior learning is of little help here. Such productive thinking is (sometimes) argued to involve insight. Gestalt psychologists even state that insight problems are a separate category of problems in their own right.
Tasks that might involve insight usually have certain features – they require something new and non-obvious to be done and in most cases they are difficult enough to predict that the initial solution attempt will be unsuccessful. When you solve a problem of this kind you often have a so called "AHA-experience" – the solution pops up all of a sudden. At one time you do not have any ideas of the answer to the problem, you do not even feel to make any progress trying out different ideas, but in the next second the problem is solved.
Fixation
Sometimes, previous experience or familiarity can even make problem solving more difficult. This is the case whenever habitual directions get in the way of finding new directions – an effect called fixation.
Functional fixedness
Functional fixedness concerns the solution of object-use problems. The basic idea is that when the usual way of using an object is emphasised, it will be far more difficult for a person to use that object in a novel manner.
An example is the two-string problem: Knut is left in a room with a chair and a pair of pliers given the task to bind two strings together that are hanging from the ceiling. The problem he faces is that he can never reach both strings at a time because they are just too far away from each other. What can Knut do?
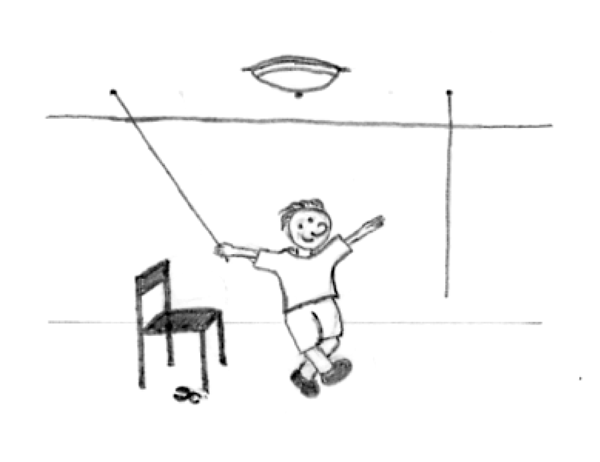
Figure \(\PageIndex{1}\): Put the two strings together by tying the pliers to one of the strings and then swing it toward the other one.
Mental fixedness
Functional fixedness as involved in the examples above illustrates a mental set – a person’s tendency to respond to a given task in a manner based on past experience. Because Knut maps an object to a particular function he has difficulties to vary the way of use (pliers as pendulum's weight).
Problem-Solving Strategies
When you are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution. Regardless of strategy, you will likely be guided, consciously or unconsciously, by your knowledge of cause-effect relations among the elements of the problem and the similarity of the problem to previous problems you have solved before. As discussed in earlier sections of this chapter, innate dispositions of the brain to look for and represent causal and similarity relations are key components of general intelligence (Koenigshofer, 2017).
A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them. For example, a well-known strategy is trial and error. The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.
| Method | Description | Example |
|---|---|---|
| Trial and error | Continue trying different solutions until problem is solved | Restarting phone, turning off WiFi, turning off bluetooth in order to determine why your phone is malfunctioning |
| Algorithm | Step-by-step problem-solving formula | Instruction manual for installing new software on your computer |
| Heuristic | General problem-solving framework | Working backwards; breaking a task into steps |
Another type of strategy is an algorithm. An algorithm is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?
A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):
- When one is faced with too much information
- When the time to make a decision is limited
- When the decision to be made is unimportant
- When there is access to very little information to use in making the decision
- When an appropriate heuristic happens to come to mind in the same moment
Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.
Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.
Problem Solving as a Search Problem
The idea of regarding problem solving as a search problem originated from Alan Newell and Herbert Simon while trying to design computer programs which could solve certain problems. This led them to develop a program called General Problem Solver which was able to solve any well-defined problem by creating heuristics on the basis of the user's input. This input consisted of objects and operations that could be done on them.
As we already know, every problem is composed of an initial state, intermediate states and a goal state (also: desired or final state), while the initial and goal states characterise the situations before and after solving the problem. The intermediate states describe any possible situation between initial and goal state. The set of operators builds up the transitions between the states. A solution is defined as the sequence of operators which leads from the initial state across intermediate states to the goal state.
The simplest method to solve a problem, defined in these terms, is to search for a solution by just trying one possibility after another (also called trial and error).
As already mentioned above, an organised search, following a specific strategy, might not be helpful for finding a solution to some ill-defined problem, since it is impossible to formalise such problems in a way that a search algorithm can find a solution.
As an example we could just take Knut and his essay: he has to find out about his own opinion and formulate it and he has to make sure he understands the sources texts. But there are no predefined operators he can use, there is no panacea how to get to an opinion and even not how to write it down.
Means-End Analysis
In Means-End Analysis you try to reduce the difference between initial state and goal state by creating sub-goals until a sub-goal can be reached directly (in computer science, what is called recursion works on this basis).
An example of a problem that can be solved by Means-End Analysis is the "Towers of Hanoi"
Figure \(\PageIndex{2}\): Towers of Hanoi with 8 discs – A well defined problem (image from Wikimedia Commons; https://commons.wikimedia.org/wiki/F..._of_Hanoi.jpeg, by User:Evanherk.licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license).
The initial state of this problem is described by the different sized discs being stacked in order of size on the first of three pegs (the “start-peg“). The goal state is described by these discs being stacked on the third pegs (the “end-peg“) in exactly the same order.

Figure \(\PageIndex{3}\): This animation shows the solution of the game "Tower of Hanoi" with four discs. (image from Wikimedia Commons; https://commons.wikimedia.org/wiki/F...of_Hanoi_4.gif; by André Karwath aka Aka; licensed under the Creative Commons Attribution-Share Alike 2.5 Generic license).
There are three operators:
- You are allowed to move one single disc from one peg to another one
- You are only able to move a disc if it is on top of one stack
- A disc cannot be put onto a smaller one.
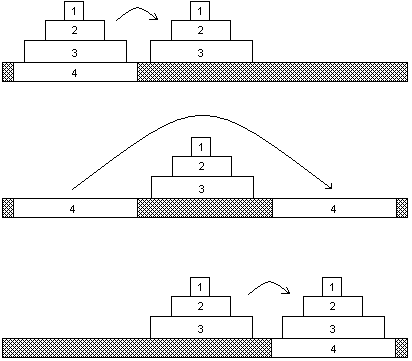
In order to use Means-End Analysis we have to create sub-goals. One possible way of doing this is described in the picture:
1. Moving the discs lying on the biggest one onto the second peg.
2. Shifting the biggest disc to the third peg.
3. Moving the other ones onto the third peg, too
You can apply this strategy again and again in order to reduce the problem to the case where you only have to move a single disc – which is then something you are allowed to do.
Strategies of this kind can easily be formulated for a computer; the respective algorithm for the Towers of Hanoi would look like this:
1. move n-1 discs from A to B
2. move disc #n from A to C
3. move n-1 discs from B to C
where n is the total number of discs, A is the first peg, B the second, C the third one. Now the problem is reduced by one with each recursive loop.
Means-end analysis is important to solve everyday-problems – like getting the right train connection: You have to figure out where you catch the first train and where you want to arrive, first of all. Then you have to look for possible changes just in case you do not get a direct connection. Third, you have to figure out what are the best times of departure and arrival, on which platforms you leave and arrive and make it all fit together.
Analogies
Analogies describe similar structures and interconnect them to clarify and explain certain relations. In a recent study, for example, a song that got stuck in your head is compared to an itching of the brain that can only be scratched by repeating the song over and over again. Useful analogies appears to be based on a psychological mapping of relations between two very disparate types of problems that have abstract relations in common. Applied to STEM problems, Gray and Holyoak (2021) state: "Analogy is a powerful tool for fostering conceptual understanding and transfer in STEM and other fields. Well-constructed analogical comparisons focus attention on the causal-relational structure of STEM concepts, and provide a powerful capability to draw inferences based on a well-understood source domain that can be applied to a novel target domain." Note that similarity between problems of different types in their abstract relations, such as causation, is a key feature of reasoning, problem-solving and inference when forming and using analogies. Recall the discussion of general intelligence in module 14.2. There, similarity relations, causal relations, and predictive relations between events were identified as key components of general intelligence, along with ability to visualize in imagination possible future actions and their probable outcomes prior to commiting to actual behavior in the physical world (Koenigshofer, 2017).
Restructuring by Using Analogies
One special kind of restructuring, the way already mentioned during the discussion of the Gestalt approach, is analogical problem solving. Here, to find a solution to one problem – the so called target problem, an analogous solution to another problem – the source problem, is presented.
An example for this kind of strategy is the radiation problem posed by K. Duncker in 1945:
As a doctor you have to treat a patient with a malignant, inoperable tumour, buried deep inside the body. There exists a special kind of ray, which is perfectly harmless at a low intensity, but at the sufficient high intensity is able to destroy the tumour – as well as the healthy tissue on his way to it. What can be done to avoid the latter?
When this question was asked to participants in an experiment, most of them couldn't come up with the appropriate answer to the problem. Then they were told a story that went something like this:
A General wanted to capture his enemy's fortress. He gathered a large army to launch a full-scale direct attack, but then learned, that all the roads leading directly towards the fortress were blocked by mines. These roadblocks were designed in such a way, that it was possible for small groups of the fortress-owner's men to pass them safely, but every large group of men would initially set them off. Now the General figured out the following plan: He divided his troops into several smaller groups and made each of them march down a different road, timed in such a way, that the entire army would reunite exactly when reaching the fortress and could hit with full strength.
Here, the story about the General is the source problem, and the radiation problem is the target problem. The fortress is analogous to the tumour and the big army corresponds to the highly intensive ray. Consequently a small group of soldiers represents a ray at low intensity. The solution to the problem is to split the ray up, as the general did with his army, and send the now harmless rays towards the tumour from different angles in such a way that they all meet when reaching it. No healthy tissue is damaged but the tumour itself gets destroyed by the ray at its full intensity.
M. Gick and K. Holyoak presented Duncker's radiation problem to a group of participants in 1980 and 1983. Only 10 percent of them were able to solve the problem right away, 30 percent could solve it when they read the story of the general before. After given an additional hint – to use the story as help – 75 percent of them solved the problem.
With this results, Gick and Holyoak concluded, that analogical problem solving depends on three steps:
1. Noticing that an analogical connection exists between the source and the target problem.
2. Mapping corresponding parts of the two problems onto each other (fortress → tumour, army → ray, etc.)
3. Applying the mapping to generate a parallel solution to the target problem (using little groups of soldiers approaching from different directions → sending several weaker rays from different directions)
Schemas
The concept that links the target problem with the analogy (the “source problem“) is called problem schema. Gick and Holyoak obtained the activation of a schema on their participants by giving them two stories and asking them to compare and summarize them. This activation of problem schemata is called “schema induction“.
The two presented texts were picked out of six stories which describe analogical problems and their solution. One of these stories was "The General."
After solving the task the participants were asked to solve the radiation problem. The experiment showed that in order to solve the target problem reading of two stories with analogical problems is more helpful than reading only one story: After reading two stories 52% of the participants were able to solve the radiation problem (only 30% were able to solve it after reading only one story, namely: “The General“).
The process of using a schema or analogy, i.e. applying it to a novel situation, is called transduction. One can use a common strategy to solve problems of a new kind.
To create a good schema and finally get to a solution using the schema is a problem-solving skill that requires practice and some background knowledge.
How Do Experts Solve Problems?
With the term expert we describe someone who devotes large amounts of his or her time and energy to one specific field of interest in which he, subsequently, reaches a certain level of mastery. It should not be of surprise that experts tend to be better in solving problems in their field than novices (people who are beginners or not as well trained in a field as experts) are. They are faster in coming up with solutions and have a higher success rate of right solutions. But what is the difference between the way experts and non-experts solve problems? Research on the nature of expertise has come up with the following conclusions:
When it comes to problems that are situated outside the experts' field, their performance often does not differ from that of novices.
Knowledge: An experiment by Chase and Simon (1973a, b) dealt with the question how well experts and novices are able to reproduce positions of chess pieces on chessboards when these are presented to them only briefly. The results showed that experts were far better in reproducing actual game positions, but that their performance was comparable with that of novices when the chess pieces were arranged randomly on the board. Chase and Simon concluded that the superior performance on actual game positions was due to the ability to recognize familiar patterns: A chess expert has up to 50,000 patterns stored in his memory. In comparison, a good player might know about 1,000 patterns by heart and a novice only few to none at all. This very detailed knowledge is of crucial help when an expert is confronted with a new problem in his field. Still, it is not pure size of knowledge that makes an expert more successful. Experts also organise their knowledge quite differently from novices.
Organization: In 1982 M. Chi and her co-workers took a set of 24 physics problems and presented them to a group of physics professors as well as to a group of students with only one semester of physics. The task was to group the problems based on their similarities. As it turned out the students tended to group the problems based on their surface structure (similarities of objects used in the problem, e.g. on sketches illustrating the problem), whereas the professors used their deep structure (the general physical principles that underlay the problems) as criteria. By recognizing the actual structure of a problem experts are able to connect the given task to the relevant knowledge they already have (e.g. another problem they solved earlier which required the same strategy).
Analysis: Experts often spend more time analyzing a problem before actually trying to solve it. This way of approaching a problem may often result in what appears to be a slow start, but in the long run this strategy is much more effective. A novice, on the other hand, might start working on the problem right away, but often has to realise that he reaches dead ends as he chose a wrong path in the very beginning.
Creative Cognition
Divergent Thinking
The term divergent thinking describes a way of thinking that does not lead to one goal, but is open-ended. Problems that are solved this way can have a large number of potential 'solutions' of which none is exactly 'right' or 'wrong', though some might be more suitable than others.
Solving a problem like this involves indirect and productive thinking and is mostly very helpful when somebody faces an ill-defined problem, i.e. when either initial state or goal state cannot be stated clearly and operators are either insufficient or not given at all.
The process of divergent thinking is often associated with creativity, and it undoubtedly leads to many creative ideas. Nevertheless, researches have shown that there is only modest correlation between performance on divergent thinking tasks and other measures of creativity. Additionally it was found that in processes resulting in original and practical inventions things like searching for solutions, being aware of structures and looking for analogies are heavily involved, too.
Figure \(\PageIndex{4}\): functional MRI images of the brains of musicians playing improvised jazz revealed that a large brain region involved in monitoring one's performance shuts down during creative improvisation, while a small region involved in organizing self-initiated thoughts and behaviors is highly activated (Image and modified caption from Wikimedia Commons. File:Creative Improvisation (24130148711).jpg; https://commons.wikimedia.org/wiki/F...130148711).jpg; by NIH Image Gallery; As a work of the U.S. federal government, the image is in the public domain.
Convergent Thinking
Convergent thinking patterns are problem solving techniques that unite different ideas or fields to find a solution. The focus of this mindset is speed, logic and accuracy, also identification of facts, reapplying existing techniques, gathering information. The most important factor of this mindset is: there is only one correct answer. You only think of two answers, namely right or wrong. This type of thinking is associated with certain science or standard procedures. People with this type of thinking have logical thinking, are able to memorize patterns, solve problems and work on scientific tests. Most school subjects sharpen this type of thinking ability.
Research shows that the creative process involves both types of thought processes.
Brain Mechanisms in Problem Solving
Presenting Neurophysiology in its entirety would be enough to fill several books. Instead, let's focus only on the aspects that are especially relevant to problem solving. Still, this topic is quite complex and problem solving cannot be attributed to one single brain area. Rather there are systems or networks of several brain areas working together to perform a specific problem solving task. This is best shown by an example, playing chess:
| Task | Location of Brain activity |
|---|---|
|
(also called the "what"-pathway of visual processing)
(also called the "where"-pathway of visual processing)
(forming new memories)
|
Table 2: Brain areas involved in a complex cognitive task.
One of the key tasks, namely planning and executing strategies, is performed by the prefrontal cortex (PFC), which also plays an important role for several other tasks correlated with problem solving. This can be made clear from the effects of damage to the PFC on ability to solve problems.
Patients with a lesion in this brain area have difficulty switching from one behavioral pattern to another. A well known example is the wisconsin card-sorting task. A patient with a PFC lesion who is told to separate all blue cards from a deck, would continue sorting out the blue ones, even if the experimenter next told him to sort out all brown cards. Transferred to a more complex problem, this person would most likely fail, because he is not flexible enough to change his strategy after running into a dead end or when the problem changes.
Another example comes from a young homemaker, who had a tumour in the frontal lobe. Even though she was able to cook individual dishes, preparing a whole family meal was an impossible task for her.
Mushiake et al. (2009) note that to achieve a goal in a complex environment, such as problem‐solving situations like those above, we must plan multiple steps of action. When planning a series of actions, we have to anticipate future outcomes that will occur as a result of each action, and, in addition, we must mentally organize the temporal sequence of events in order to achieve the goal. These researchers investigated the role of lateral prefrontal cortex (PFC) in problem solving in monkeys. They found that "PFC neurons reflected final goals and immediate goals during the preparatory period. [They] also found some PFC neurons reflected each of all the forthcoming steps of actions during the preparatory period and they increased their [neural] activity step by step during the execution period. [Furthermore, they] found that the transient increase in synchronous activity of PFC neurons was involved in goal subgoal transformations. [They concluded] that the PFC is involved primarily in the dynamic representation of multiple future events that occur as a consequence of behavioral actions in problem‐solving situations" (Mushiake et al., 2009, p. 1). In other words, the prefrontal cortex represents in our imagination the sequence of events following each step that we take in solving a particular problem, guiding us step by step to the solution.
As the examples above illustrate, the structure of our brain is of great importance regarding problem solving, i.e. cognitive life. But how was our cognitive apparatus designed? How did perception-action integration as a central species-specific property of humans come about? The answer, as argued extensively in earlier sections of this book, is, of course, natural selection and other forces of genetic evolution. Clearly, animals and humans with genes facilitating brain organization that led to good problem solving skills would be favored by natural selection over genes responsible for brain organization less adept at solving problems. We became equipped with brains organized for effective problem solving because flexible abilities to solve a wide range of problems presented by the environment enhanced ability to survive, to compete for resources, to escape predators, and to reproduce (see chapter on Evolution and Genetics in this text).
In short, good problem solving mechanisms in brains designed for the real world gave a competitive advantage and increased biological fitness. Consequently, humans (and many other animals to a lesser degree) have "innate ability to problem-solve in the real world. Solving real world problems in real time given constraints posed by one's environment is crucial for survival . . . Real world problem solving (RWPS) is different from those that occur in a classroom or in a laboratory during an experiment. They are often dynamic and discontinuous, accompanied by many starts and stops . . . Real world problems are typically ill-defined, and even when they are well-defined, often have open-ended solutions . . . RWPS is quite messy and involves a tight interplay between problem solving, creativity, and insight . . . In psychology and neuroscience, problem-solving broadly refers to the inferential steps taken by an agent [human, animal, or computer] that leads from a given state of affairs to a desired goal state" (Sarathy, 2018, p. 261-2). According to Sarathy (2018), the initial stage of RWPS requires defining the problem and generating a representation of it in working memory. This stage involves activation of parts of the "prefrontal cortex (PFC), default mode network (DMN), and the dorsal anterior cingulate cortex (dACC)." The DMN includes the medial prefrontal cortex, posterior cingulate cortex, and the inferior parietal lobule. Other structures sometimes considered part of the network are the lateral temporal cortex, hippocampal formation, and the precuneus. This network of structures is called "default mode" because these structures show increased activity when one is not engaged in focused, attentive, goal-directed actions, but rather a "resting state" (a baseline default state) and show decreased neural activity when one is focused and attentive to a particular goal-directed behavior (Raichle, et al., 2001).
Moral Reasoning
Jeurissen, et al., (2014) examined a special type of reasoning, moral reasoning, using TMS (Transcranial Magnetic Stimulation). The dorsolateral prefrontal cortex (DLPFC) and temporal-parietal junction (TPJ) have both been shown to be involved in moral judgments, but this study by Jeurissen, et al., (2014) uses TMS to tease out the different roles these brain areas play in different scenarios involving moral dilemmas.
Moral dilemmas have been categorized by researchers as moral-impersonal (e.g., trolley or switch dilemma--save the lives of five workmen at the expense of the life of one by switching train to another track) and moral-personal dilemmas (e.g., footbridge dilemma--push a stranger in front of a train to save the lives of five others). In the first scenario, the person just pulls a switch resulting in death of one person to save five, but in the second, the person pushes the victim to their death to save five others.
Dual-process theory proposes that moral decision-making involves two components: an automatic emotional response and a voluntary application of a utilitarian decision-rule (in this case, one death to save five people is worth it). The thought of being responsible for the death of another person elicits an aversive emotional response, but at the same time, cognitive reasoning favors the utilitarian option. Decision making and social cognition are often associated with the DLPFC. Neurons in the prefrontal cortex have been found to be involved in cost-benefit analysis and categorize stimuli based on the predicted consequences.
Theory-of-mind (TOM) is a cognitive mechanism which is used when one tries to understand and explain the knowledge, beliefs, and intention of others. TOM and empathy are often associated with TPJ functioning.
In the article by Jeurissen, et al., (2014), brain activity is measured by BOLD. BOLD refers to Blood-oxygen-level-dependent imaging, or BOLD-contrast imaging, which is a way to measure neural activity in different brain areas in MRI images.
Greene et al., 2001 (Links to an external site.), 2004 (Links to an external site.) reported that activity in the prefrontal cortex is thought to be important for the cognitive reasoning process, which can counteract the automatic emotional response that occurs in moral dilemmas like the one in Jeurissen, et al., (2014). Greene et al. (2001) (Links to an external site.) found that the medial portions of the medial frontal gyrus, the posterior cingulate gyrus, and the bilateral angular gyrus showed a higher BOLD response in the moral-personal condition than the moral-impersonal condition. The right middle frontal gyrus and the bilateral parietal lobes showed a lower BOLD response in the moral-personal condition than in the moral impersonal. Furthermore, Greene et al. (2004) (Links to an external site.) showed an increased BOLD response for the bilateral amygdale in personal compared to the impersonal dilemmas.
Given the role of the prefrontal cortex in moral decision-making, Jeurissen, et al., (2014) hypothesized that when magnetically stimulating prefrontal cortex, they will selectively influence the decision process of the moral personal dilemmas because the cognitive reasoning for which the DLPFC is important is disrupted, thereby releasing the emotional component making it more influential in the resolution of the dilemma. Because the activity in the TPJ is related to emotional processing and theory of mind (Saxe and Kanwisher, 2003 (Links to an external site.); Young et al., 2010 (Links to an external site.)), Jeurissen, et al., (2014) hypothesized that when magnetically stimulating this area, the TPJ, during a moral decision, this will selectively influence the decision process of moral-impersonal dilemmas.
Results of this study by Jeurissen, et al., (2014) showed an important role of the TPJ in moral judgment. Experiments using fMRI (Greene et al., 2004 (Links to an external site.)), have found the cingulate cortex to be involved in moral judgment. In earlier studies, the cingulate cortex was found to be involved in the emotional response. Since the moral-personal dilemmas are more emotionally salient, the higher activity observed for TPJ in the moral-personal condition (more emotional) is consistent with this view. Another area that is hypothesized to be associated with the emotional response is the temporal cortex. In this study by Jeurissen, et al., (2014), magnetic stimulation of the right DLPFC and right TPJ shows roles for right DLPFC (reasoning and utilitarian) and right TPJ (emotion) in moral impersonal and moral personal dilemmas respectively. TMS over the right DLPFC (disrupting neural activity here) leads to behavior changes consistent with less cognitive control over emotion. After right DLPFC stimulation, participants show less feelings of regret than after magnetic stimulation of the right TPJ. This last finding indicates that the right DLPFC is involved in evaluating the outcome of the decision process. In summary, this experiment by Jeurissen, et al., (2014) adds to evidence of a critical role of right DLPFC and right TPJ in moral decision-making and supports that hypothesis that the former is involved in judgments based on cognitive reasoning and anticipation of outcomes, whereas the latter is involved in emotional processing related to moral dilemmas.
Summary
Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. The brain mechanisms involved in problem solving vary to some degree depending upon the sensory modalities involved in the problem and its solution, however, the prefrontal cortex is one brain region that appears to be centrally involved in all problem-solving. The prefrontal cortex is required for flexible shifts in attention, for representing the problem in working memory, and for holding steps in problem solving in working memory along with representations of future consequences of those actions permitting planning and execution of plans. Also implicated is the Default Mode Network (DMN) including medial prefrontal cortex, posterior cingulate cortex, and the inferior parietal module, and sometimes the lateral temporal cortex, hippocampus, and the precuneus. Moral reasoning involves a different set of brain areas, primarily the dorsolateral prefrontal cortex (DLPFC) and temporal-parietal junction (TPJ).
Review Questions
- A specific formula for solving a problem is called ________.
- an algorithm
- a heuristic
- a mental set
- trial and error
- A mental shortcut in the form of a general problem-solving framework is called ________.
- an algorithm
- a heuristic
- a mental set
- trial and error
References
Gray, M. E., & Holyoak, K. J. (2021). Teaching by analogy: From theory to practice. Mind, Brain, and Education, 15 (3), 250-263.
Hunt, L. T., Behrens, T. E., Hosokawa, T., Wallis, J. D., & Kennerley, S. W. (2015). Capturing the temporal evolution of choice across prefrontal cortex. Elife, 4, e11945.
Mushiake, H., Sakamoto, K., Saito, N., Inui, T., Aihara, K., & Tanji, J. (2009). Involvement of the prefrontal cortex in problem solving. International review of neurobiology, 85, 1-11.
Jeurissen, D., Sack, A. T., Roebroeck, A., Russ, B. E., & Pascual-Leone, A. (2014). TMS affects moral judgment, showing the role of DLPFC and TPJ in cognitive and emotional processing. Frontiers in neuroscience, 8, 18.
Kahneman, D. (2011). Thinking, fast and slow. New York: Farrar, Straus, and Giroux.
Koenigshofer, K. A. (2017). General Intelligence: Adaptation to Evolutionarily Familiar Abstract Relational Invariants, Not to Environmental or Evolutionary Novelty. The Journal of Mind and Behavior, 119-153.
Pratkanis, A. (1989). The cognitive representation of attitudes. In A. R. Pratkanis, S. J. Breckler, & A. G. Greenwald (Eds.), Attitude structure and function (pp. 71–98). Hillsdale, NJ: Erlbaum.
Raichle, M. E., MacLeod, A. M., Snyder, A. Z., Powers, W. J., Gusnard, D. A., & Shulman, G. L. (2001). A default mode of brain function. Proceedings of the National Academy of Sciences, 98(2), 676-682.
Sawyer, K. (2011). The cognitive neuroscience of creativity: a critical review. Creat. Res. J. 23, 137–154. doi: 10.1080/10400419.2011.571191
Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases. Science, 185(4157), 1124–1131.
Brain Mechanisms in Problem Solving
Hunt, L. T., Behrens, T. E., Hosokawa, T., Wallis, J. D., & Kennerley, S. W. (2015). Capturing the temporal evolution of choice across prefrontal cortex. Elife, 4, e11945.
Mushiake, H., Sakamoto, K., Saito, N., Inui, T., Aihara, K., & Tanji, J. (2009). Involvement of the prefrontal cortex in problem solving. International review of neurobiology, 85, 1-11. https://www.sciencedirect.com/scienc...74774209850010
Sawyer, K. (2011). The cognitive neuroscience of creativity: a critical review. Creat. Res. J. 23, 137–154. doi: 10.1080/10400419.2011.571191
Attributions
"Overview," "Problem Solving Strategies," adapted from Problem Solving by OpenStax Colleg licensed CC BY-NC 4.0 via OER Commons
"Defining Problems," "Problem Solving as a Search Problem," "Creative Cognition," "Brain Mechanisms in Problem-Solving" adapted by Kenneth A. Koenigshofer, Ph.D., from 2.1, 2.2, 2.3, 2.4, 2.5, 2.6 in Cognitive Psychology and Cognitive Neuroscience (Wikibooks) https://en.wikibooks.org/wiki/Cognit...e_Neuroscience; unless otherwise noted, LibreTexts content is licensed by CC BY-NC-SA 3.0. Legal; the LibreTexts libraries are Powered by MindTouch
Moral Reasoning was written by Kenneth A. Koenigshofer, Ph.D, Chaffey College.
Categories and Concepts
By Gregory Murphy, New York UniversityPeople form mental concepts of categories of objects, which permit them to respond appropriately to new objects they encounter. Most concepts cannot be strictly defined but are organized around the “best” examples or prototypes, which have the properties most common in the category. Objects fall into many different categories, but there is usually a most salient one, called the basic-level category, which is at an intermediate level of specificity (e.g., chairs, rather than furniture or desk chairs). Concepts are closely related to our knowledge of the world, and people can more easily learn concepts that are consistent with their knowledge. Theories of concepts argue either that people learn a summary description of a whole category or else that they learn exemplars of the category. Recent research suggests that there are different ways to learn and represent concepts and that they are accomplished by different neural systems.
- Understand the problems with attempting to define categories.
- Understand typicality and fuzzy category boundaries.
- Learn about theories of the mental representation of concepts.
- Learn how knowledge may influence concept learning.
Introduction

Consider the following set of objects: some dust, papers, a computer monitor, two pens, a cup, and an orange. What do these things have in common? Only that they all happen to be on my desk as I write this. This set of things can be considered a category, a set of objects that can be treated as equivalent in some way. But, most of our categories seem much more informative—they share many properties. For example, consider the following categories: trucks, wireless devices, weddings, psychopaths, and trout. Although the objects in a given category are different from one another, they have many commonalities. When you know something is a truck, you know quite a bit about it. The psychology of categories concerns how people learn, remember, and use informative categories such as trucks or psychopaths.
The mental representations we form of categories are called concepts. There is a category of trucks in the actual physical world, and I also have a concept of trucks in my head. We assume that people’s concepts correspond more or less closely to the actual category, but it can be useful to distinguish the two, as when someone’s concept is not really correct.
Concepts are at the core of intelligent behavior. We expect people to be able to know what to do in new situations and when confronting new objects. If you go into a new classroom and see chairs, a blackboard, a projector, and a screen, you know what these things are and how they will be used. You’ll sit on one of the chairs and expect the instructor to write on the blackboard or project something onto the screen. You do this even if you have never seen any of these particular objects before, because you have concepts of classrooms, chairs, projectors, and so forth, that tell you what they are and what you’re supposed to do with them. Furthermore, if someone tells you a new fact about the projector—for example, that it has a halogen bulb—you are likely to extend this fact to other projectors you encounter. In short, concepts allow you to extend what you have learned about a limited number of objects to a potentially infinite set of entities (i.e. generalization). Notice how categories and concepts arise from similarity, one of the abstract features of the world that has been genetically internalized into the brain during evolution, creating an innate disposition of brains to search for and to represent groupings of similar things, forming one component of general intelligence. One property of the human brain that distinguishes us from other animals is the high degrees of abstraction in similarity relations that the human brain is capable of encoding compared to the brains of non-human animals (Koenigshofer, 2017).
Simpler organisms, such as animals and human infants, also have concepts (Mareschal, Quinn, & Lea, 2010). Squirrels may have a concept of predators, for example, that is specific to their own lives and experiences. However, animals likely have many fewer concepts and cannot understand complex concepts such as mortgages or musical instruments.
You know thousands of categories, most of which you have learned without careful study or instruction. Although this accomplishment may seem simple, we know that it isn’t, because it is difficult to program computers to solve such intellectual tasks. If you teach a learning program that a robin, a swallow, and a duck are all birds, it may not recognize a cardinal or peacock as a bird. However, this shortcoming in computers may be at least partially overcome when the type of processing used is parallel distributed processing as employed in artificial neural networks (Koenigshofer, 2017), discussed in this chapter. As we’ll shortly see, the problem for computers is that objects in categories are often surprisingly diverse.
Nature of Categories

Traditionally, it has been assumed that categories are well-defined. This means that you can give a definition that specifies what is in and out of the category. Such a definition has two parts. First, it provides the necessary features for category membership: What must objects have in order to be in it? Second, those features must be jointly sufficient for membership: If an object has those features, then it is in the category. For example, if I defined a dog as a four-legged animal that barks, this would mean that every dog is four-legged, an animal, and barks, and also that anything that has all those properties is a dog.
Unfortunately, it has not been possible to find definitions for many familiar categories. Definitions are neat and clear-cut; the world is messy and often unclear. For example, consider our definition of dogs. In reality, not all dogs have four legs; not all dogs bark. I knew a dog that lost her bark with age (this was an improvement); no one doubted that she was still a dog. It is often possible to find some necessary features (e.g., all dogs have blood and breathe), but these features are generally not sufficient to determine category membership (you also have blood and breathe but are not a dog).
Even in domains where one might expect to find clear-cut definitions, such as science and law, there are often problems. For example, many people were upset when Pluto was downgraded from its status as a planet to a dwarf planet in 2006. Upset turned to outrage when they discovered that there was no hard-and-fast definition of planethood: “Aren’t these astronomers scientists? Can’t they make a simple definition?” In fact, they couldn’t. After an astronomical organization tried to make a definition for planets, a number of astronomers complained that it might not include accepted planets such as Neptune and refused to use it. If everything looked like our Earth, our moon, and our sun, it would be easy to give definitions of planets, moons, and stars, but the universe has not conformed to this ideal.
Fuzzy Categories
Borderline Items
Experiments also showed that the psychological assumptions of well-defined categories were not correct. Hampton (1979) asked subjects to judge whether a number of items were in different categories. He did not find that items were either clear members or clear nonmembers. Instead, he found many items that were just barely considered category members and others that were just barely not members, with much disagreement among subjects. Sinks were barely considered as members of the kitchen utensil category, and sponges were barely excluded. People just included seaweed as a vegetable and just barely excluded tomatoes and gourds. Hampton found that members and nonmembers formed a continuum, with no obvious break in people’s membership judgments. If categories were well defined, such examples should be very rare. Many studies since then have found such borderline members that are not clearly in or clearly out of the category.
McCloskey and Glucksberg (1978) found further evidence for borderline membership by asking people to judge category membership twice, separated by two weeks. They found that when people made repeated category judgments such as “Is an olive a fruit?” or “Is a sponge a kitchen utensil?” they changed their minds about borderline items—up to 22 percent of the time. So, not only do people disagree with one another about borderline items, they disagree with themselves! As a result, researchers often say that categories are fuzzy, that is, they have unclear boundaries that can shift over time.
Typicality
A related finding that turns out to be most important is that even among items that clearly are in a category, some seem to be “better” members than others (Rosch, 1973). Among birds, for example, robins and sparrows are very typical. In contrast, ostriches and penguins are very atypical (meaning not typical). If someone says, “There’s a bird in my yard,” the image you have will be of a smallish passerine bird such as a robin, not an eagle or hummingbird or turkey.
You can find out which category members are typical merely by asking people. Table 1 shows a list of category members in order of their rated typicality. Typicality is perhaps the most important variable in predicting how people interact with categories. The following text box is a partial list of what typicality influences.
We can understand the two phenomena of borderline members and typicality as two sides of the same coin. Think of the most typical category member: This is often called the category prototype. Items that are less and less similar to the prototype become less and less typical. At some point, these less typical items become so atypical that you start to doubt whether they are in the category at all. Is a rug really an example of furniture? It’s in the home like chairs and tables, but it’s also different from most furniture in its structure and use. From day to day, you might change your mind as to whether this atypical example is in or out of the category. So, changes in typicality ultimately lead to borderline members.
 Table 2: Text Box 1
Table 2: Text Box 1Source of Typicality
Intuitively, it is not surprising that robins are better examples of birds than penguins are, or that a table is a more typical kind of furniture than is a rug. But given that robins and penguins are known to be birds, why should one be more typical than the other? One possible answer is the frequency with which we encounter the object: We see a lot more robins than penguins, so they must be more typical. Frequency does have some effect, but it is actually not the most important variable (Rosch, Simpson, & Miller, 1976). For example, I see both rugs and tables every single day, but one of them is much more typical as furniture than the other.
The best account of what makes something typical comes from Rosch and Mervis’s (1975) family resemblance theory. They proposed that items are likely to be typical if they (a) have the features that are frequent in the category and (b) do not have features frequent in other categories. Let’s compare two extremes, robins and penguins. Robins are small flying birds that sing, live in nests in trees, migrate in winter, hop around on your lawn, and so on. Most of these properties are found in many other birds. In contrast, penguins do not fly, do not sing, do not live in nests or in trees, do not hop around on your lawn. Furthermore, they have properties that are common in other categories, such as swimming expertly and having wings that look and act like fins. These properties are more often found in fish than in birds.

According to Rosch and Mervis, then, it is not because a robin is a very common bird that makes it typical. Rather, it is because the robin has the shape, size, body parts, and behaviors that are very common (i.e. most similar) among birds—and not common among fish, mammals, bugs, and so forth.
In a classic experiment, Rosch and Mervis (1975) made up two new categories, with arbitrary features. Subjects viewed example after example and had to learn which example was in which category. Rosch and Mervis constructed some items that had features that were common in the category and other items that had features less common in the category. The subjects learned the first type of item before they learned the second type. Furthermore, they then rated the items with common features as more typical. In another experiment, Rosch and Mervis constructed items that differed in how many features were shared with a different category. The more features were shared, the longer it took subjects to learn which category the item was in. These experiments, and many later studies, support both parts of the family resemblance theory.
Category Hierarchies
Many important categories fall into hierarchies, in which more concrete categories are nested inside larger, abstract categories. For example, consider the categories: brown bear, bear, mammal, vertebrate, animal, entity. Clearly, all brown bears are bears; all bears are mammals; all mammals are vertebrates; and so on. Any given object typically does not fall into just one category—it could be in a dozen different categories, some of which are structured in this hierarchical manner. Examples of biological categories come to mind most easily, but within the realm of human artifacts, hierarchical structures can readily be found: desk chair, chair, furniture, artifact, object.
Brown (1958), a child language researcher, was perhaps the first to note that there seems to be a preference for which category we use to label things. If your office desk chair is in the way, you’ll probably say, “Move that chair,” rather than “Move that desk chair” or “piece of furniture.” Brown thought that the use of a single, consistent name probably helped children to learn the name for things. And, indeed, children’s first labels for categories tend to be exactly those names that adults prefer to use (Anglin, 1977).
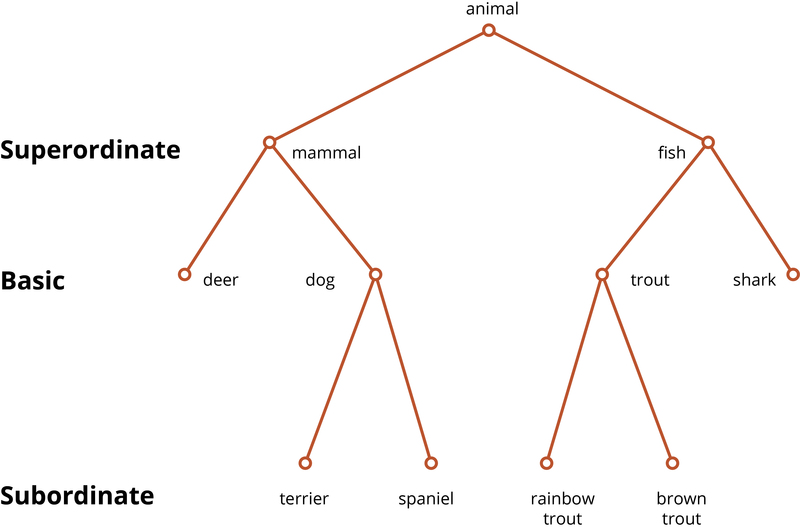
This preference is referred to as a preference for the basic level of categorization, and it was first studied in detail by Eleanor Rosch and her students (Rosch, Mervis, Gray, Johnson, & Boyes-Braem, 1976). The basic level represents a kind of Goldilocks effect, in which the category used for something is not too small (northern brown bear) and not too big (animal), but is just right (bear). The simplest way to identify an object’s basic-level category is to discover how it would be labeled in a neutral situation. Rosch et al. (1976) showed subjects pictures and asked them to provide the first name that came to mind. They found that 1,595 names were at the basic level, with 14 more specific names (subordinates) used. Only once did anyone use a more general name (superordinate). Furthermore, in printed text, basic-level labels are much more frequent than most subordinate or superordinate labels (e.g., Wisniewski & Murphy, 1989).
The preference for the basic level is not merely a matter of labeling. Basic-level categories are usually easier to learn. As Brown noted, children use these categories first in language learning, and superordinates are especially difficult for children to fully acquire.[1] People are faster at identifying objects as members of basic-level categories (Rosch et al., 1976).
Rosch et al. (1976) initially proposed that basic-level categories cut the world at its joints, that is, merely reflect the big differences between categories like chairs and tables or between cats and mice that exist in the world. However, it turns out that which level is basic is not universal. North Americans are likely to use names like tree, fish, and bird to label natural objects. But people in less industrialized societies seldom use these labels and instead use more specific words, equivalent to elm, trout, and finch (Berlin, 1992). Because Americans and many other people living in industrialized societies know so much less than our ancestors did about the natural world, our basic level has “moved up” to what would have been the superordinate level a century ago. Furthermore, experts in a domain often have a preferred level that is more specific than that of non-experts. Birdwatchers see sparrows rather than just birds, and carpenters see roofing hammers rather than just hammers (Tanaka & Taylor, 1991). This all suggests that the preferred level is not (only) based on how different categories are in the world, but that people’s knowledge and interest in the categories has an important effect.
One explanation of the basic-level preference is that basic-level categories are more differentiated: The category members are similar to one another, but they are different from members of other categories (Murphy & Brownell, 1985; Rosch et al., 1976). (The alert reader will note a similarity to the explanation of typicality I gave above. However, here we’re talking about the entire category and not individual members.) Chairs are pretty similar to one another, sharing a lot of features (legs, a seat, a back, similar size and shape); they also don’t share that many features with other furniture. Superordinate categories are not as useful because their members are not very similar to one another. What features are common to most furniture? There are very few. Subordinate categories are not as useful, because they’re very similar to other categories: Desk chairs are quite similar to dining room chairs and easy chairs. As a result, it can be difficult to decide which subordinate category an object is in (Murphy & Brownell, 1985). Experts can differ from novices in which categories are the most differentiated, because they know different things about the categories, therefore changing how similar the categories are.
[1] This is a controversial claim, as some say that infants learn superordinates before anything else (Mandler, 2004). However, if true, then it is very puzzling that older children have great difficulty learning the correct meaning of words for superordinates, as well as in learning artificial superordinate categories (Horton & Markman, 1980; Mervis, 1987). However, it seems fair to say that the answer to this question is not yet fully known.
Theories of Concept Representation
Now that we know these facts about the psychology of concepts, the question arises of how concepts are mentally represented. There have been two main answers. The first, somewhat confusingly called the prototype theory suggests that people have a summary representation of the category, a mental description that is meant to apply to the category as a whole. (The significance of summary will become apparent when the next theory is described.) This description can be represented as a set of weighted features (Smith & Medin, 1981). The features are weighted by their frequency in the category. For the category of birds, having wings and feathers would have a very high weight; eating worms would have a lower weight; living in Antarctica would have a lower weight still, but not zero, as some birds do live there.
The idea behind prototype theory is that when you learn a category, you learn a general description that applies to the category as a whole: Birds have wings and usually fly; some eat worms; some swim underwater to catch fish. People can state these generalizations, and sometimes we learn about categories by reading or hearing such statements (“The kimodo dragon can grow to be 10 feet long”).
When you try to classify an item, you see how well it matches that weighted list of features. For example, if you saw something with wings and feathers fly onto your front lawn and eat a worm, you could (unconsciously) consult your concepts and see which ones contained the features you observed. This example possesses many of the highly weighted bird features, and so it should be easy to identify as a bird.
This theory readily explains the phenomena we discussed earlier. Typical category members have more, higher-weighted features. Therefore, it is easier to match them to your conceptual representation. Less typical items have fewer or lower-weighted features (and they may have features of other concepts). Therefore, they don’t match your representation as well (less similarity). This makes people less certain in classifying such items. Borderline items may have features in common with multiple categories or not be very close to any of them. For example, edible seaweed does not have many of the common features of vegetables but also is not close to any other food concept (meat, fish, fruit, etc.), making it hard to know what kind of food it is.
A very different account of concept representation is the exemplar theory (exemplar being a fancy name for an example; Medin & Schaffer, 1978). This theory denies that there is a summary representation. Instead, the theory claims that your concept of vegetables is remembered examples of vegetables you have seen. This could of course be hundreds or thousands of exemplars over the course of your life, though we don’t know for sure how many exemplars you actually remember.
How does this theory explain classification? When you see an object, you (unconsciously) compare it to the exemplars in your memory, and you judge how similar it is to exemplars in different categories. For example, if you see some object on your plate and want to identify it, it will probably activate memories of vegetables, meats, fruit, and so on. In order to categorize this object, you calculate how similar it is to each exemplar in your memory. These similarity scores are added up for each category. Perhaps the object is very similar to a large number of vegetable exemplars, moderately similar to a few fruit, and only minimally similar to some exemplars of meat you remember. These similarity scores are compared, and the category with the highest score is chosen.[2]
Why would someone propose such a theory of concepts? One answer is that in many experiments studying concepts, people learn concepts by seeing exemplars over and over again until they learn to classify them correctly. Under such conditions, it seems likely that people eventually memorize the exemplars (Smith & Minda, 1998). There is also evidence that close similarity to well-remembered objects has a large effect on classification. Allen and Brooks (1991) taught people to classify items by following a rule. However, they also had their subjects study the items, which were richly detailed. In a later test, the experimenters gave people new items that were very similar to one of the old items but were in a different category. That is, they changed one property so that the item no longer followed the rule. They discovered that people were often fooled by such items. Rather than following the category rule they had been taught, they seemed to recognize the new item as being very similar to an old one and so put it, incorrectly, into the same category.
Many experiments have been done to compare the prototype and exemplar theories. Overall, the exemplar theory seems to have won most of these comparisons. However, the experiments are somewhat limited in that they usually involve a small number of exemplars that people view over and over again. It is not so clear that exemplar theory can explain real-world classification in which people do not spend much time learning individual items (how much time do you spend studying squirrels? or chairs?). Also, given that some part of our knowledge of categories is learned through general statements we read or hear, it seems that there must be room for a summary description separate from exemplar memory.
Many researchers would now acknowledge that concepts are represented through multiple cognitive systems. For example, your knowledge of dogs may be in part through general descriptions such as “dogs have four legs.” But you probably also have strong memories of some exemplars (your family dog, Lassie) that influence your categorization. Furthermore, some categories also involve rules (e.g., a strike in baseball). How these systems work together is the subject of current study.
[2] Actually, the decision of which category is chosen is more complex than this, but the details are beyond this discussion.
Knowledge
The final topic has to do with how concepts fit with our broader knowledge of the world. We have been talking very generally about people learning the features of concepts. For example, they see a number of birds and then learn that birds generally have wings, or perhaps they remember bird exemplars. From this perspective, it makes no difference what those exemplars or features are—people just learn them. But consider two possible concepts of buildings and their features in Table 2.

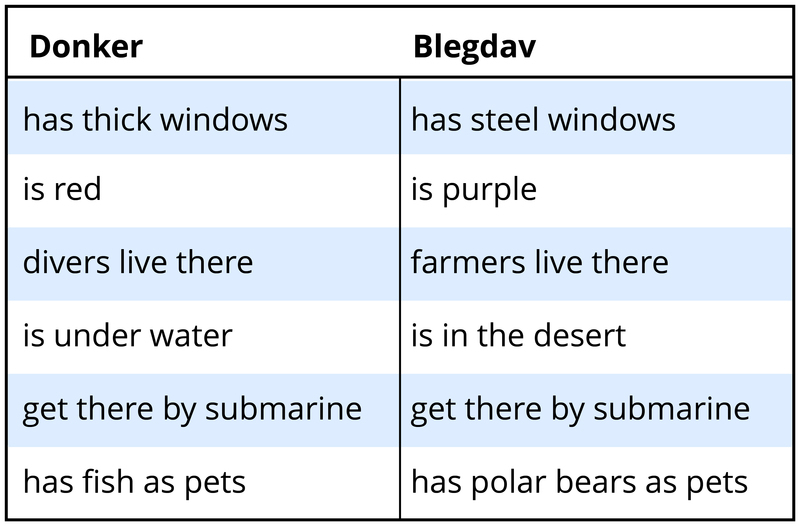
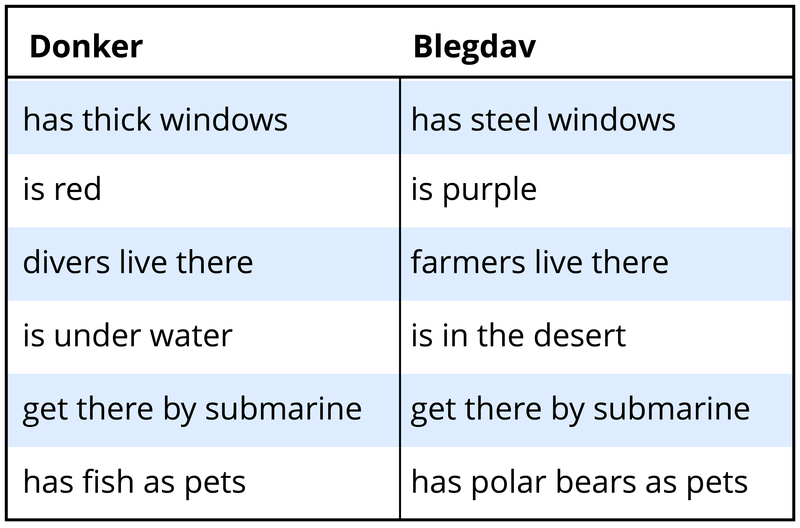
Imagine you had to learn these two concepts by seeing exemplars of them, each exemplar having some of the features listed for the concept (as well as some idiosyncratic features). Learning the donker concept would be pretty easy. It seems to be a kind of underwater building, perhaps for deep-sea explorers. Its features seem to go together. In contrast, the blegdav doesn’t really make sense. If it’s in the desert, how can you get there by submarine, and why do they have polar bears as pets? Why would farmers live in the desert or use submarines? What good would steel windows do in such a building? This concept seems peculiar. In fact, if people are asked to learn new concepts that make sense, such as donkers, they learn them quite a bit faster than concepts such as blegdavs that don’t make sense (Murphy & Allopenna, 1994). Furthermore, the features that seem connected to one another (such as being underwater and getting there by submarine) are learned better than features that don’t seem related to the others (such as being red).
Such effects demonstrate that when we learn new concepts, we try to connect them to the knowledge we already have about the world. If you were to learn about a new animal that doesn’t seem to eat or reproduce, you would be very puzzled and think that you must have gotten something wrong. By themselves, the prototype and exemplar theories don’t predict this. They simply say that you learn descriptions or exemplars, and they don’t put any constraints on what those descriptions or exemplars are. However, the knowledge approach to concepts emphasizes that concepts are meant to tell us about real things in the world, and so our knowledge of the world is used in learning and thinking about concepts.
We can see this effect of knowledge when we learn about new pieces of technology. For example, most people could easily learn about tablet computers (such as iPads) when they were first introduced by drawing on their knowledge of laptops, cell phones, and related technology. Of course, this reliance on past knowledge can also lead to errors, as when people don’t learn about features of their new tablet that weren’t present in their cell phone or expect the tablet to be able to do something it can’t.
One important aspect of people’s knowledge about categories is called psychological essentialism (Gelman, 2003; Medin & Ortony, 1989). People tend to believe that some categories—most notably natural kinds such as animals, plants, or minerals—have an underlying property that is found only in that category and that causes its other features. Most categories don’t actually have essences, but this is sometimes a firmly held belief. For example, many people will state that there is something about dogs, perhaps some specific gene or set of genes, that all dogs have and that makes them bark, have fur, and look the way they do. Therefore, decisions about whether something is a dog do not depend only on features that you can easily see but also on the assumed presence of this cause.
Belief in an essence can be revealed through experiments describing fictional objects. Keil (1989) described to adults and children a fiendish operation in which someone took a raccoon, dyed its hair black with a white stripe down the middle, and implanted a “sac of super-smelly yucky stuff” under its tail. The subjects were shown a picture of a skunk and told that this is now what the animal looks like. What is it? Adults and children over the age of 4 all agreed that the animal is still a raccoon. It may look and even act like a skunk, but a raccoon cannot change its stripes (or whatever!)—it will always be a raccoon.
Importantly, the same effect was not found when Keil described a coffeepot that was operated on to look like and function as a bird feeder. Subjects agreed that it was now a bird feeder. Artifacts don’t have an essence.
Signs of essentialism include (a) objects are believed to be either in or out of the category, with no in-between; (b) resistance to change of category membership or of properties connected to the essence; and (c) for living things, the essence is passed on to progeny.
Essentialism is probably helpful in dealing with much of the natural world, but it may be less helpful when it is applied to humans. Considerable evidence suggests that people think of gender, racial, and ethnic groups as having essences, which serves to emphasize the difference between groups and even justify discrimination (Hirschfeld, 1996). Historically, group differences were described by inheriting the blood of one’s family or group. “Bad blood” was not just an expression but a belief that negative properties were inherited and could not be changed. After all, if it is in the nature of “those people” to be dishonest (or clannish or athletic ...), then that could hardly be changed, any more than a raccoon can change into a skunk.
Research on categories of people is an exciting ongoing enterprise, and we still do not know as much as we would like to about how concepts of different kinds of people are learned in childhood and how they may (or may not) change in adulthood. Essentialism doesn’t apply only to person categories, but it is one important factor in how we think of groups.
Summary
Concepts are central to our everyday thought. When we are planning for the future or thinking about our past, we think about specific events and objects in terms of their categories. If you’re visiting a friend with a new baby, you have some expectations about what the baby will do, what gifts would be appropriate, how you should behave toward it, and so on. Knowing about the category of babies helps you to effectively plan and behave when you encounter this child you’ve never seen before. Such inferences from knowledge about a category are highly adaptive and an important component of thinking and intelligence.
Learning about those categories is a complex process that involves seeing exemplars (babies), hearing or reading general descriptions (“Babies like black-and-white pictures”), general knowledge (babies have kidneys), and learning the occasional rule (all babies have a rooting reflex). Current research is focusing on how these different processes take place in the brain. It seems likely that these different aspects of concepts are accomplished by different neural structures (Maddox & Ashby, 2004). However, it is clear that the brain is genetically predisposed to seek out similarities in the environment and to represent groupings of things forming categories that can be used to make inferences about new instances of the category which have never been encountered before. In this way knowledge is organized and expectations from this knowledge allow improved adaptation to newly encountered environmental objects and situations by virtue of their similarity to a known category previously formed (Koenigshofer, 2017).
Another interesting topic is how concepts differ across cultures. As different cultures have different interests and different kinds of interactions with the world, it seems clear that their concepts will somehow reflect those differences. On the other hand, the structure of the physical world also imposes a strong constraint on what kinds of categories are actually useful. The interplay of culture, the environment, and basic cognitive processes in establishing concepts has yet to be fully investigated.
Discussion Questions
- Pick a couple of familiar categories and try to come up with definitions for them. When you evaluate each proposal (a) is it in fact accurate as a definition, and (b) is it a definition that people might actually use in identifying category members?
- For the same categories, can you identify members that seem to be “better” and “worse” members? What about these items makes them typical and atypical?
- Going around the room, point to some common objects (including things people are wearing or brought with them) and identify what the basic-level category is for that item. What are superordinate and subordinate categories for the same items?
- List some features of a common category such as tables. The knowledge view suggests that you know reasons for why these particular features occur together. Can you articulate some of those reasons? Do the same thing for an animal category.
- Choose three common categories: a natural kind, a human artifact, and a social event. Discuss with class members from other countries or cultures whether the corresponding categories in their cultures differ. Can you make a hypothesis about when such categories are likely to differ and when they are not?
Vocabulary
- Basic-level category
- The neutral, preferred category for a given object, at an intermediate level of specificity.
- Category
- A set of entities that are equivalent in some way. Usually the items are similar to one another.
- Concept
- The mental representation of a category.
- Exemplar
- An example in memory that is labeled as being in a particular category.
- Psychological essentialism
- The belief that members of a category have an unseen property that causes them to be in the category and to have the properties associated with it.
- Typicality
- The difference in “goodness” of category members, ranging from the most typical (the prototype) to borderline members.
References
- Allen, S. W., & Brooks, L. R. (1991). Specializing the operation of an explicit rule.Journal of Experimental Psychology: General, 120, 3–19.
- Anglin, J. M. (1977). Word, object, and conceptual development. New York, NY: W. W. Norton.
- Berlin, B. (1992). Ethnobiological classification: Principles of categorization of plants and animals in traditional societies. Princeton, NJ: Princeton University Press.
- Brown, R. (1958). How shall a thing be called? Psychological Review, 65, 14–21.
- Gelman, S. A. (2003). The essential child: Origins of essentialism in everyday thought. Oxford, UK: Oxford University Press.
- Hampton, J. A. (1979). Polymorphous concepts in semantic memory. Journal of Verbal Learning and Verbal Behavior, 18, 441–461.
- Hirschfeld, L. A. (1996). Race in the making: Cognition, culture, and the child's construction of human kinds. Cambridge, MA: MIT Press.
- Horton, M. S., & Markman, E. M. (1980). Developmental differences in the acquisition of basic and superordinate categories. Child Development, 51, 708–719.
- Keil, F. C. (1989). Concepts, kinds, and cognitive development. Cambridge, MA: MIT Press.
- Koenigshofer, K. A. (2017). General Intelligence: Adaptation to Evolutionarily Familiar Abstract Relational Invariants, Not to Environmental or Evolutionary Novelty. The Journal of Mind and Behavior, 38(2):119-153.
- Maddox, W. T., & Ashby, F. G. (2004). Dissociating explicit and procedural-based systems of perceptual category learning. Behavioural Processes, 66, 309–332.
- Mandler, J. M. (2004). The foundations of mind: Origins of conceptual thought. Oxford, UK: Oxford University Press.
- Mareschal, D., Quinn, P. C., & Lea, S. E. G. (Eds.) (2010). The making of human concepts. Oxford, UK: Oxford University Press.
- McCloskey, M. E., & Glucksberg, S. (1978). Natural categories: Well defined or fuzzy sets? Memory & Cognition, 6, 462–472.
- Medin, D. L., & Ortony, A. (1989). Psychological essentialism. In S. Vosniadou & A. Ortony (Eds.), Similarity and analogical reasoning (pp. 179–195). Cambridge, UK: Cambridge University Press.
- Medin, D. L., & Schaffer, M. M. (1978). Context theory of classification learning. Psychological Review, 85, 207–238.
- Mervis, C. B. (1987). Child-basic object categories and early lexical development. In U. Neisser (Ed.), Concepts and conceptual development: Ecological and intellectual factors in categorization (pp. 201–233). Cambridge, UK: Cambridge University Press.
- Murphy, G. L., & Allopenna, P. D. (1994). The locus of knowledge effects in concept learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 20, 904–919.
- Murphy, G. L., & Brownell, H. H. (1985). Category differentiation in object recognition: Typicality constraints on the basic category advantage. Journal of Experimental Psychology: Learning, Memory, and Cognition, 11, 70–84.
- Norenzayan, A., Smith, E. E., Kim, B. J., & Nisbett, R. E. (2002). Cultural preferences for formal versus intuitive reasoning. Cognitive Science, 26, 653–684.
- Rosch, E., & Mervis, C. B. (1975). Family resemblance: Studies in the internal structure of categories. Cognitive Psychology, 7, 573–605.
- Rosch, E., Mervis, C. B., Gray, W., Johnson, D., & Boyes-Braem, P. (1976). Basic objects in natural categories. Cognitive Psychology, 8, 382–439.
- Rosch, E., Simpson, C., & Miller, R. S. (1976). Structural bases of typicality effects. Journal of Experimental Psychology: Human Perception and Performance, 2, 491–502.
- Rosch, E. H. (1973). On the internal structure of perceptual and semantic categories. In T. E. Moore (Ed.), Cognitive development and the acquisition of language (pp. 111–144). New York, NY: Academic Press.
- Smith, E. E., & Medin, D. L. (1981). Categories and concepts. Cambridge, MA: Harvard University Press.
- Smith, J. D., & Minda, J. P. (1998). Prototypes in the mist: The early epochs of category learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 24, 1411–1436.
- Tanaka, J. W., & Taylor, M. E. (1991). Object categories and expertise: Is the basic level in the eye of the beholder? Cognitive Psychology, 15, 121–149.
- Wisniewski, E. J., & Murphy, G. L. (1989). Superordinate and basic category names in discourse: A textual analysis. Discourse Processes, 12, 245–261.
Attributions
Authors

- Gregory Murphy is Professor of Psychology at New York University. He previously taught at the University of Illinois and Brown University. His research focuses on concepts and reasoning, and he is the author of The Big Book of Concepts (MIT Press, 2002).
Creative Commons License
Adapted by Kenneth Koenigshofer, PhD, from Categories and Concepts by Gregory Murphy, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. Permissions beyond the scope of this license may be available in our Licensing Agreement.
How to cite this Noba module using APA Style
Murphy, G. (2021). Categories and concepts. In R. Biswas-Diener & E. Diener (Eds), Noba textbook series: Psychology. Champaign, IL: DEF publishers. Retrieved from http://noba.to/6vu4cpkt






