4.3: Associations
- Page ID
- 21223
Classical cognitive science has been profoundly influenced by seventeenth-century Cartesian philosophy (Descartes, 1996, 2006). The Cartesian view that thinking is equivalent to performing mental logic—that it is a mental discourse of computation or calculation (Hobbes, 1967)—has inspired the logicism that serves as the foundation of the classical approach. Fundamental classical notions, such as the assumption that cognition is the result of rule-governed symbol manipulation (Craik, 1943) or that innate knowledge is required to solve problems of underdetermination (Chomsky, 1965, 1966), have resulted in the classical being viewed as a newer variant of Cartesian rationalism (Paivio, 1986). One key classical departure from Descartes is its rejection of dualism.
Classical cognitive science has appealed to recursive rules to permit finite devices to generate an infinite variety of potential behaviour. Classical cognitive science is the modern rationalism, and one of the key ideas that it employs is recursion. Connectionist cognitive science has very different philosophical roots. Connectionism is the modern form of empiricist philosophy (Berkeley, 1710; Hume, 1952; Locke, 1977), where knowledge is not innate, but is instead provided by sensing the world. “No man’s knowledge here can go beyond his experience” (Locke, 1977, p. 83). If recursion is fundamental to the classical approach’s rationalism, then what notion is fundamental to connectionism’s empiricism? The key idea is association: different ideas can be linked together, so that if one arises, then the association between them causes the other to arise as well.
For centuries, philosophers and psychologists have studied associations empirically, through introspection (Warren, 1921). These introspections have revealed the existence of sequences of thought that occur during thinking. Associationism attempted to determine the laws that would account for these sequences of thought.
The earliest detailed introspective account of such sequences of thought can be found in the 350 BC writings of Aristotle (Sorabji, 2006, p. 54): “Acts of recollection happen because one change is of a nature to occur after another.” For Aristotle, ideas were images (Cummins, 1989). He argued that a particular sequence of images occurs either because this sequence is a natural consequence of the images, or because the sequence has been learned by habit. Recall of a particular memory, then, is achieved by cuing that memory with the appropriate prior images, which initiate the desired sequence of images. “Whenever we recollect, then, we undergo one of the earlier changes, until we undergo the one after which the change in question habitually occurs” (Sorabji, 2006, p. 54). Aristotle’s analysis of sequences of thought is central to modern mnemonic techniques for remembering ordered lists (Lorayne, 2007; Lorayne & Lucas, 1974).
Aristotle noted that recollection via initiating a sequence of mental images could be a deliberate and systematic process. This was because the first image in the sequence could be selected so that it would be recollected fairly easily. Recall of the sequence, or of the target image at the end of the sequence, was then dictated by lawful relationships between adjacent ideas. Thus Aristotle invented laws of association.
Aristotle considered three different kinds of relationships between the starting image and its successor: similarity, opposition, and (temporal) contiguity:
And this is exactly why we hunt for the successor, starting in our thoughts from the present or from something else, and from something similar, or opposite, or neighbouring. By this means recollection occurs. (Sorabji, 2006, p. 54)
In more modern associationist theories, Aristotle’s laws would be called the law of similarity, the law of contrast, and the law of contiguity or the law of habit.
Aristotle’s theory of memory was essentially ignored for many centuries (Warren, 1921). Instead, pre-Renaissance and Renaissance Europe were more interested in the artificial memory—mnemonics—that was the foundation of Greek oratory. These techniques were rediscovered during the Middle Ages in the form of Ad Herennium, a circa 86 BC text on rhetoric that included a section on enhancing the artificial memory (Yates, 1966). Ad Herennium described the mnemonic techniques invented by Simonides circa 500 BC. While the practice of mnemonics flourished during the Middle Ages, it was not until the seventeenth century that advances in associationist theories of memory and thought began to flourish.
The rise of modern associationism begins with Thomas Hobbes (Warren, 1921). Hobbes’ (1967) notion of thought as mental discourse was based on his observation that thinking involved an orderly sequence of ideas. Hobbes was interested in explaining how such sequences occurred. While Hobbes’ own work was very preliminary, it inspired more detailed analyses carried out by the British empiricists who followed him.
Empiricist philosopher John Locke coined the phrase association of ideas, which first appeared as a chapter title in the fourth edition of An Essay Concerning Human Understanding (Locke, 1977). Locke’s work was an explicit reaction against Cartesian philosophy (Thilly, 1900); his goal was to establish experience as the foundation of all thought. He noted that connections between simple ideas might not reflect a natural order. Locke explained this by appealing to experience: Ideas that in themselves are not at all of kin, come to be so united in some men’s minds that it is very hard to separate them, they always keep in company, and the one no sooner at any time comes into the understanding but its associate appears with it. (Locke, 1977, p. 122) Eighteenth-century British empiricists expanded Locke’s approach by exploring and debating possible laws of association. George Berkeley (1710) reiterated Aristotle’s law of contiguity and extended it to account for associations involving different modes of sensation. David Hume (1852) proposed three different laws of association: resemblance, contiguity in time or place, and cause or effect. David Hartley, one of the first philosophers to link associative laws to brain function, saw contiguity as the primary source of associations and ignored Hume’s law of resemblance (Warren, 1921).
Debates about the laws of association continued into the nineteenth century. James Mill (1829) only endorsed the law of contiguity, and explicitly denied Hume’s laws of cause and effect or resemblance. Mill’s ideas were challenged and modified by his son, John Stuart Mill. In his revised version of his father’s book (Mill & Mill, 1869), Mill posited a completely different set of associative laws, which included a reintroduction of Hume’s law of similarity. He also replaced his father’s linear, mechanistic account of complex ideas with a “mental chemistry” that endorsed nonlinear emergence. This is because in this mental chemistry, when complex ideas were created via association, the resulting whole was more than just the sum of its parts. Alexander Bain (1855) refined the associationism of John Stuart Mill, proposing four different laws of association and attempting to reduce all intellectual processes to these laws. Two of these were the familiar laws of contiguity and of similarity.
Bain was the bridge between philosophical and psychological associationism (Boring, 1950). He stood,
exactly at a corner in the development of psychology, with philosophical psychology stretching out behind, and experimental physiological psychology lying ahead, in a new direction. The psychologists of the twentieth century can read much of Bain with hearty approval; perhaps John Locke could have done the same. (Boring, 1950, p. 240)
One psychologist who approved of Bain was William James; he frequently cited Bain in his Principles of Psychology (James, 1890a). Chapter 14 of this work provided James’ own treatment of associationism. James criticized philosophical associationism’s emphasis on associations between mental contents. James proposed a mechanistic, biological theory of associationism instead, claiming that associations were made between brain states:
We ought to talk of the association of objects, not of the association of ideas. And so far as association stands for a cause, it is between processes in the brain—it is these which, by being associated in certain ways, determine what successive objects shall be thought. (James, 1890a, p. 554, original italics)
James (1890a) attempted to reduce other laws of association to the law of contiguity, which he called the law of habit and expressed as follows: “When two elementary brain-processes have been active together or in immediate succession, one of them, on reoccurring, tends to propagate its excitement into the other” (p. 566). He illustrated the action of this law with a figure (James, 1890a, p. 570, Figure 40), a version of which is presented as Figure 4-1.
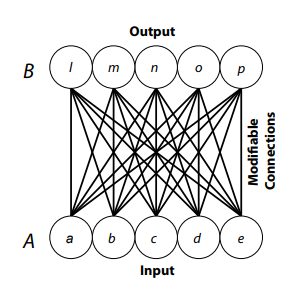
Figure 4-1. A distributed memory, initially described by James (1890a) but also part of modern connectionism.
Figure 4-1 illustrates two ideas, A and B, each represented as a pattern of activity in its own set of neurons. A is represented by activity in neurons a, b, c, d, and e; B is represented by activity in neurons l, m, n, o, and p. The assumption is that A represents an experience that occurred immediately before B. When B occurs, activating its neurons, residual activity in the neurons representing A permits the two patterns to be associated by the law of habit. That is, the “tracts” connecting the neurons (the “modifiable connections” in Figure 4-1) have their strengths modified.
The ability of A’s later activity to reproduce B is due to these modified connections between the two sets of neurons.
The thought of A must awaken that of B, because a, b, c, d, e, will each and all discharge into l through the paths by which their original discharge took place. Similarly they will discharge into m, n, o, and p; and these latter tracts will also each reinforce the other’s action because, in the experience B, they have already vibrated in unison. (James, 1890a, p. 569)
James’ (1890a) biological account of association reveals three properties that are common to modern connectionist networks. First, his system is parallel: more than one neuron can be operating at the same time. Second, his system is convergent: the activity of one of the output neurons depends upon receiving or summing the signals sent by multiple input neurons. Third, his system is distributed: the association between A and B is the set of states of the many “tracts” illustrated in Figure 4-1; there is not just a single associative link.
James’s (1890a) law of habit was central to the basic mechanism proposed by neuroscientist Donald Hebb (1949) for the development of cell assemblies. Hebb provided a famous modern statement of James’ law of habit:
When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased. (Hebb, 1949, p. 62)
This makes explicit the modern connectionist idea that learning is modifying the strength of connections between processors. Hebb’s theory inspired the earliest computer simulations of memory systems akin to the one proposed by James (Milner, 1957; Rochester et al., 1956). These simulations revealed a critical role for inhibition that led Hebb (1959) to revise his theory. Modern neuroscience has discovered a phenomenon called long-term potentiation that is often cited as a biologically plausible instantiation of Hebb’s theory (Brown, 1990; Gerstner & Kistler, 2002; Martinez & Derrick, 1996; van Hemmen & Senn, 2002).
The journey from James through Hebb to the first simulations of memory (Milner, 1957; Rochester et al., 1956) produced a modern associative memory system called the standard pattern associator (McClelland, 1986). The standard pattern associator, which is structurally identical to Figure 4-1, is a memory capable of learning associations between pairs of input patterns (Steinbuch, 1961; Taylor, 1956) or learning to associate an input pattern with a categorizing response (Rosenblatt, 1962; Selfridge, 1956; Widrow & Hoff, 1960).
The standard pattern associator is empiricist in the sense that its knowledge is acquired by experience. Usually the memory begins as a blank slate: all of the connections between processors start with weights equal to zero. During a learning phase, pairs of to-be-associated patterns simultaneously activate the input and output units in Figure 4-1. With each presented pair, all of the connection weights— the strength of each connection between an input and an output processor—are modified by adding a value to them. This value is determined in accordance with some version of Hebb’s (1949) learning rule. Usually, the value added to a weight is equal to the activity of the processor at the input end of the connection, multiplied by the activity of the processor at the output end of the connection, and multiplied by some fractional value called a learning rate. The mathematical details of such learning are provided in Chapter 9 of Dawson (2004).
The standard pattern associator is called a distributed memory because its knowledge is stored throughout all the connections in the network, and because this one set of connections can store several different associations. During a recall phase, a cue pattern is used to activate the input units. This causes signals to be sent through the connections in the network. These signals are equal to the activation value of an input unit multiplied by the weight of the connection through which the activity is being transmitted. Signals received by the output processors are used to compute net input, which is simply the sum of all of the incoming signals. In the standard pattern associator, an output unit’s activity is equal to its net input. If the memory is functioning properly, then the pattern of activation in the output units will be the pattern that was originally associated with the cue pattern.
The standard pattern associator is the cornerstone of many models of memory created after the cognitive revolution (Anderson, 1972; Anderson et al., 1977; Eich, 1982; Hinton & Anderson, 1981; Murdock, 1982; Pike, 1984; Steinbuch, 1961; Taylor, 1956). These models are important, because they use a simple principle—James’ (1890a, 1890b) law of habit—to model many subtle regularities of human memory, including errors in recall. In other words, the standard pattern associator is a kind of memory that has been evaluated with the different kinds of evidence cited in Chapters 2 and 3, in an attempt to establish strong equivalence.
The standard pattern associator also demonstrates another property crucial to modern connectionism, graceful degradation. How does this distributed model behave if it is presented with a noisy cue, or with some other cue that was never tested during training? It generates a response that has the same degree of noise as its input (Dawson, 1998, Table 3-1). That is, there is a match between the quality of the memory’s input and the quality of its output.
The graceful degradation of the standard pattern associator reveals that it is sensitive to the similarity of noisy cues to other cues that were presented during training. Thus modern pattern associators provide some evidence for James’ (1890a) attempt to reduce other associative laws, such as the law of similarity, to the basic law of habit or contiguity.
In spite of the popularity and success of distributed associative memories as models of human learning and recall (Hinton & Anderson, 1981), they are extremely limited in power. When networks learn via the Hebb rule, they produce errors when they are overtrained, are easily confused by correlated training patterns, and do not learn from their errors (Dawson, 2004). An error-correcting rule called the delta rule (Dawson, 2004; Rosenblatt, 1962; Stone, 1986; Widrow & Hoff, 1960) can alleviate some of these problems, but it does not eliminate them. While association is a fundamental notion in connectionist models, other notions are required by modern connectionist cognitive science. One of these additional ideas is nonlinear processing.


