Four teenagers live on your street. Each is willing to shovel snow from one driveway each day. Their "willingness to shovel" valuations (supply) are: Jean, $10; Kevin, $9; Liam, $7; Margaret, $5. Several households are interested in having their driveways shoveled, and their willingness to pay values (demand) are: Jones, $8; Kirpinsky, $4; Lafleur, $7.50; Murray, $6.
- Draw the implied supply and demand curves as step functions.
- How many driveways will be shoveled in equilibrium?
- Compute the maximum possible sum for the consumer and supplier surpluses.
- If a new (wealthy) family arrives on the block, that is willing to pay $12 to have their driveway cleared, recompute the answers to parts (a), (b), and (c).
Consider a market where supply curve is horizontal at P=10 and the demand curve has intercepts 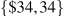 , and is defined by the relation P=34–Q.
, and is defined by the relation P=34–Q.
- Illustrate the market geometrically.
- Impose a tax of $2 per unit on the good so that the supply curve is now P=12. Illustrate the new equilibrium quantity.
- Illustrate in your diagram the tax revenue generated.
- Illustrate the deadweight loss of the tax.
Next, consider an example of DWL in the labour market. Suppose the demand for labour is given by the fixed gross wage 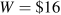 . The supply is given by W=0.8L, indicating that the supply curve goes through the origin with a slope of 0.8.
. The supply is given by W=0.8L, indicating that the supply curve goes through the origin with a slope of 0.8.
- Illustrate the market geometrically.
- Calculate the supplier surplus, knowing that the equilibrium is L=20.
- Optional: Suppose a wage tax is imposed that produces a net-of-tax wage equal to
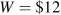 . This can be seen as a downward shift in the demand curve. Illustrate the new quantity supplied and the new supplier's surplus.
. This can be seen as a downward shift in the demand curve. Illustrate the new quantity supplied and the new supplier's surplus.
Governments are in the business of providing information to potential buyers. The first serious provision of information on the health consequences of tobacco use appeared in the United States Report of the Surgeon General in 1964.
- How would you represent this intervention in a supply and demand for tobacco diagram?
- Did this intervention "correct" the existing market demand?
In deciding to drive a car in the rush hour, you think about the cost of gas and the time of the trip.
- Do you slow down other people by driving?
- Is this an externality, given that you yourself are suffering from slow traffic?
Suppose that our local power station burns coal to generate electricity. The demand and supply functions for electricity are given by P=12–0.5Q and P=2+0.5Q, respectively. The demand curve has intercepts 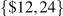 and the supply curve intercept is at $2 with a slope of one half. However, for each unit of electricity generated, there is an externality. When we factor this into the supply side of the market, the real social cost is increased by $1 per unit. That is, the supply curve shifts upwards by $1, and now takes the form P=3+0.5Q.
and the supply curve intercept is at $2 with a slope of one half. However, for each unit of electricity generated, there is an externality. When we factor this into the supply side of the market, the real social cost is increased by $1 per unit. That is, the supply curve shifts upwards by $1, and now takes the form P=3+0.5Q.
- Illustrate the free-market equilibrium.
- Illustrate the efficient (i.e. socially optimal) level of production.
Your local dry cleaner, Bleached Brite, is willing to launder shirts at its cost of $1.00 per shirt. The neighbourhood demand for this service is P=5–0.005Q, knowing that the demand intercepts are 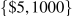 .
.
- Illustrate the market equilibrium.
- Suppose that, for each shirt, Bleached Brite emits chemicals into the local environment that cause $0.25 damage per shirt. This means the full cost of each shirt is $1.25. Illustrate graphically the socially optimal number of shirts to be cleaned.
- Optional: Calculate the socially optimal number of shirts to be cleaned.
The supply curve for agricultural labour is given by W=6+0.1L, where W is the wage (price per unit) and L the quantity traded. Employers are willing to pay a wage of $12 to all workers who are willing to work at that wage; hence the demand curve is W=12.
- Illustrate the market equilibrium, if you are told that the equilibrium occurs where L=60.
- Compute the supplier surplus at this equilibrium.
Optional: The market demand for vaccine XYZ is given by P=36–Q and the supply conditions are P=20; so $20 represents the true cost of supplying a unit of vaccine. There is a positive externality associated with being vaccinated, and the real societal value is known and given by P=36–(1/2)Q. This new demand curve represents the true value to society of each vaccination. This is reflected in the private value demand curve rotating upward around the price intercept of $36.
- Illustrate the private and social demand curves on a diagram, with intercept values calculated.
- What is the market solution to this supply and demand problem?
- What is the socially optimal number of vaccinations?


