Exercise \(\PageIndex{1}\)
Consider the use of the word web for the World-Wide Web and the use of the word root to mean 'source' (as in the root of all evil). What is the basis for these semantic extensions? What do they have in common?
So far we've looked at how the meanings of words can be extended, both by adult speakers and by babies learning the language, in ways that make them more or less general. In this section we'll consider two other general kinds of conceptual relations that permit word meanings to be extended: similarity and various kinds of close association.
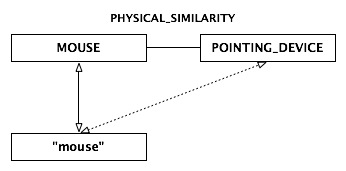
First consider the situation that arose when computers were first outfitted with pointing devices to be manipulated in one hand by moving them across a pad and pushing one of their buttons. The noun that came to be used for these devices, mouse, was based on the resemblance of the devices to the animal: the general size and shape and the tail-like cable. Thus the meaning of the word mouse was extended on the basis of the physical similarity between one category (the animal) and another (the pointing device). Extension of a word's meaning on the basis of similarity is known as metaphoric extension. This figure illustrates the process.
Here is another computer-related example. When computer software started providing users with sets of choices that they could select from, the word that emerged for these lists was menu. The metaphoric extension was based on the similarity between a restaurant menu, a list of food and drink choices, and the list of choices that the computer user was to select from.
One frequent use of metaphor is the application of a word referring to an object category to a more abstract semantic category, something not physical at all. Consider the structure of taxonomies as in this example from the last section. If we turn the figure illustrating the taxonomy over, it resembles a tree, with the most general category as the root and the most specific categories the leaves. This is in fact how cognitive scientists refer to structures like this; tree is applied to the whole structure, root is applied to the point where all of thebranches begin, and leaf is applied to the point beyond which there are no more branches. Note that a taxonomy is not a physical thing at all, so with metaphoric extension we have now taken common nouns such as tree and leaf outside of the realm of the physical entirely.
This example also illustrates how metaphor often operates on two entire domains, each with its own elements and internal structure. The source domain is the one that is being used to understand the (usually more complex) target domain. In this example, the source domain is tree, the target domain taxonomy. The metaphor is based on multiple similarities between the domains: correspondences (or mappings) between the elements (leaves and specific concepts, for example) and the relations between the elements (branches join the root to the leaves; generalization links join the most general concept to the more specific ones).
Metonymy
The word for 'language' may be related to other, less abstract words, for example, the word for 'tongue' (as in Spanish), the word for 'mouth' (as in Oromo), the word for 'voice' (as in Tzeltal). Assuming that the 'language' sense is an extension of the more basic sense in each case, what's the basis of this extension?
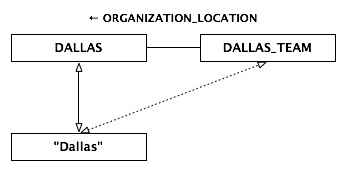
A somewhat more complicated possibility for extending a word meaning is based on a quite different conceptual relation, not similarity between the instances of the two categories but a strong association between them. This is referred to as metonymic extension. Consider the association between an organization (an abstract concept), such as a sports team or a government, and its base location. While we can refer to the organization directly using its name, we often find it convenient to use the name of the location to refer to the organization.
- Dallas won yesterday's game.
- No one is sure what Moscow's response will be.
This figure illustrates the first example of metonymy.
Another conceptual relation that permits metonymy is that between a document and the content of the document. Thus the word bookrefers to a physical object: a collection of sheets with printing or pictures on them that is bound together. But we can also use the word to refer to the informational content of the physical book. Compare the uses of the word in these two sentences.
- This book is almost too heavy to lift.
- I don't understand this book at all.
In the first example, the speaker is clearly referring to the physical object, in the second example to the information contained in the physical object. In a case like this, metonymic extension allows a noun referring to a physical object to refer to something more abstract.
Insulting with Metonymy
Metonymy may also be used in situations where an alternative to an existing noun is called for, perhaps as a very informal or insulting term. Examples are the use of wheels to mean 'car', brain to mean 'intelligent person', and asshole to mean 'person' in an insulting context. In these examples the relevant conceptual relation is between a whole and a part. (There is much more going on than just this, especially in the last example, because the choice of the particular part is obviously also relevant!)
Metonymy may also come into play "on the fly", when a speaker is using language creatively. Here's an example from Fauconnier (1985). One waitress in a restaurant is speaking to another.
- The omelet left without paying.
Of course the speaker doesn't mean that some cooked eggs left the restaurant; she is referring to a customer. The conceptual relation that is the basis for the metonymic extension in this case is the relation between a customer and the customer's order. Note that omelet would only be expected to get this interpretation in the appropriate context; that same person would not normally be called the omelet.
Metonymy in Children's Nouns?
Finally we see apparent examples of metonymy in the speech of young children. Andrés, who was learning both English and Spanish, used the Spanish word luna ('moon' in adult Spanish) during his second year to refer not only to the moon and crescent shapes but also to the pens or pencils used to draw crescent shapes. It appears that he has extended the word on the basis of the relation between an image and the instrument used to produce the image. But, as always, we must be careful in interpreting children's utterances. Most of Andrés' utterances during this period consisted of a single word. When he said "luna" apparently referring to a pen, did he really mean something more like "use this to draw a crescent"? We have no simple way of knowing.




