4.2: Theory Constrution
- Last updated
- Save as PDF
- Page ID
- 76192
Learning Objectives
By the end of this section, you will be able to:
- Remember the definition of theory
- Understand how a theory is generated
- Apply a model theory
- Analyze increasingly complex theories
- Evaluate statements to determine if they are theories or not
- Create a theory
Remembering the Definition of Theory
In its simplest form, a theory is an explanation of how the world works. Now, there are many ways in which the world works: natural, physical, chemical, biological, social, political, historical and the list can go on. For example, political scientists are interested in how elected officials behave during campaigns (Warren 2008). One theory is that elected officials are more responsive to voters during campaigns. A reason an elected official is more likely to spend time in their communities, host town halls, and meet with stakeholders during campaigns is because they want to demonstrate how they are proactively serving their constituents.
In addition to suggesting how some aspect of the world works, theories also lead us to explore possibilities. For example, what happens if an elected official spends less time or more time with their constituents during campaigns? One could argue that by spending less time with constituents during the campaign, an elected official is less likely to earn their support. On the other hand, if an elected official spends more time with constituents, support for their campaigns will increase.
In constructing a theory, we are engaging in a process of observing the world and proposing how the world works.
A theory is a set of assumptions about constants, variables, and the relationship between variables. In other words, a theory is a statement about the relationship between two objects with all other objects held constant. In a complex world with a multitude of objects surrounding us, it can be difficult to focus on just two objects. Thus, for a theory to be useful, we need to be able to focus on at least two objects and the relationship between those objects. So, how can we focus on just two objects and their relationship? To help us focus, we can hold all other objects constant. Constant means that all other objects, except for the two objects we are interested in, are held still.
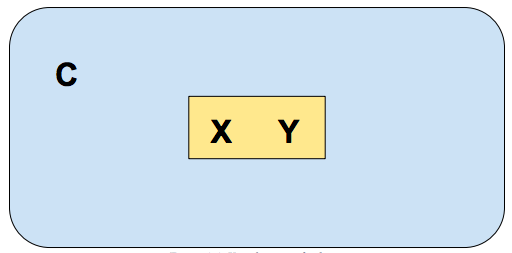
Figure \(\PageIndex{1}\): Visualization of a theory
The letter X and the letter Y represent the two objects of interest, while the yellow box symbolizes that a relationship exists between the two objects. The reason a theory needs to have at least two objects is because a theory is an explanation of how one object relates to another object. If we are just focused on one object, then we do not have a theory. Rather, we are observing an object for its own sake.
Understanding How a Theory is Generated
A theory can be generated in three ways. First, a theory can be generated without reference to any existing theory. This is very rare since a theory requires two objects. These two objects exist because theories have attempted to explain the objects. Second, a theory can be an extension to an existing theory. Given the multitude of theories that already exist, it is common for someone to rely on and extend an existing theory. Third, a theory can be the contradiction of an existing theory. While it is common to build on an existing theory, it can be just as common to use contradiction to generate a theory.
Applying a Model Theory
A model theory is a statement that two objects, X and Y, exists and that a relationship exists between X and Y. With this model theory, how can we apply it to topics or subjects we are interested in? Let’s consider three examples.
First, we may be interested in the relationship between political actors in a democracy. The two political actors we are interested in is the government and the media. We could argue that the media is represented by object X while the government represented by object Y. A theory should explain why and how there is a relationship between the media and the government. Additionally, the theory should assume that other political actors are held constant, so we can focus on the relationship between the media and the government.
Our next example is the relationship between information and voters in a representative democracy. In this example, information is represented by X while voters are represented by Y. Why would a voter have a relationship with information? One reason this relationship would exist is because voters use information to make decisions on how to vote. Another reason is that information is sent to voters from candidates and campaigns in order to influence a voter’s decision.
Analyzing Increasingly Complex Theories
The core of any theory is the relationship between a minimum of two objects of interest. However, theories can be more complex by having additional variables that can serve different roles in a theory. For example, imagine we have a theory that states a relationship between three variables: X, Y, and Z. The relationship between these three objects could be described in a multitude of ways, but let’s focus on three potential relationships: X and Y, Y and Z, and X and Z.
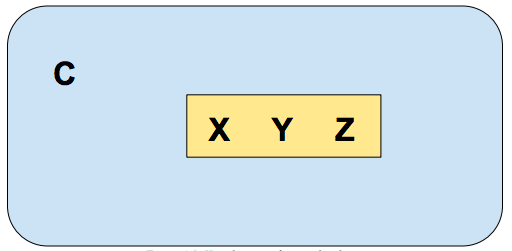
Figure \(\PageIndex{2}\): Visualization of a complex theory
Creating a Theory
Theories are statements of relationships between two concepts. There are three characteristics of theories that we should seek to achieve when proposing a theory. First, a theory should be general, meaning that it can include a variety of operationalizations and geographic contexts. Let’s compare a specific theory to a general theory. A specific theory may be focused on how voters in a midwestern U.S. state decide to support a presidential candidate. A researcher would then propose hypotheses, collect evidence, analyze the data, and make some findings. The knowledge generated from this process would be useful for future researchers want to better understand the Midwestern voter, to political campaigns that try to reach these voters, and to news outlets that want to provide background information to a new story at the written. The question is: How can this theory be extended beyond the voter living in the Midwest of the United States?
To answer this question, we need to propose a more general theory. A general theory can explore how voters respond to national-level candidates. A researcher would again propose hypotheses, collect evidence, analyze the data, and generate some results. Given that there are voters in Europe, South America, Africa, Asia, Oceania, as well as North America, we can collect evidence from voters living in countries in these regions of the world. In analyzing the data, research and a fine a lot of differences but they also might find a lot of similarities between voters responding to national level candidates in their countries. The similarities and differences can help us better understand the relationship declared by the theory. So, by using a more general theory we could subsume the more specific theory that was originally discussed.
It’s not to say that a specific theory is less useful than a general theory, because you can see how the two ideas intertwine. By starting with the general theory, we can think more broadly about how it applies in different times, places, and subjects. From here, we can narrow down to specific places that are of greater interest to us knowing that we are feeding into the broader exploration and knowledge creation process.
The second characteristic of theories is to try to make them parsimonious. Parsimonious means frugal or to use something sparingly. When generating a theory, the point is to keep it simple because when you make a theory too complicated it’s more difficult to see its generality and, as will discuss momentarily, it’s falsifiability. Let’s walk through two examples of theories from the most parsimonious to the least parsimonious so we can fix in our mind the utility of maintaining simplicity. Consider that I have a theory about gender and representation. My hypothesis is that gender has an influence on who runs and who wins elected office. Therefore, in a study of voters, male candidates are more likely than female candidates to be elected to office. To explore this hypothesis, I would collect data, analyze it, and reach some initial findings that either support or do not support my hypothesis. This is a relatively straightforward theory in the sense that an attribute of a candidate influences a voter support for that candidate.
Now, let’s make our original theory more complicated. Let’s consider a theory about candidate attributes, voter behavior, campaign strategies, election processes, and policy outcomes. What should strike you is that we have more than two concepts; here we have five concepts. In proposing this theory, it could be argued that these concepts are linearly related: candidates attributes affect voter behavior, which influences campaign strategies, which then shapes electoral processes, and finally then alters policy outcomes. A well-reasoned explanation for these connections may be convincing to some. However, the length of the theoretical chain makes it susceptible to criticism. For example, are candidate attributes the only thing that influences voting behavior? Moreover, does voter behavior influence campaign strategies or is the relationship the other way around? Therefore, given the complexity of the theory, it can be difficult to discern the nature of the relationships between different concepts. Hence, parsimony is an important characteristic to consider when developing a theory to make clear and bring into relationships within a theory.
Falsifiability is the third characteristic of theories we want to explain. Falsifiability is the ability of a theory to be shown as false. Why should a theory be falsifiable? A theory that is not falsifiable means that no amount of reason or evidence can lead a researcher to suggest that their original theory is incorrect. If reason or evidence cannot be presented, then a theory cannot be scrutinized. Thus, the scientific method process is broken because new information cannot be brought to challenge a theory and suggest a new theory for us to be considered. At some point, enough reason and evidence are brought to bear to suggest a theory is now a law. But the law is not ironclad, it just becomes accepted by the scientific community for the time being. Establishing a theory as a law does not preclude it from being falsified in the future when new times, places, and contexts may challenge the findings from theories.
Together, generality, parsimoniousness, and falsifiability work together to make theories integral parts of the scientific method and the discovery and creation of new knowledge.


