1.2: The Spatial Perspective

At the heart of the spatial perspective is the question of “where,” but there are a number of different ways to answer this question. Relative location refers to the location of a place relative to other places, and we commonly use relative location when giving directions to people. We might instruct them to turn “by the gas station on the corner,” or say that we live “in the dorm across from the fountain.” Another way to describe a place is by referring to its absolute location. Absolute location references an exact point on Earth and commonly uses specific coordinates like latitude and longitude. Lines of latitude and longitude are imaginary lines that circle the globe and form the geographic coordinate system (Figure \(\PageIndex{1}\)). Lines of latitude run laterally, parallel to the equator, and measure distances north or south of the equator. Lines of longitude, on the other hand, converge at the poles and measure distances east and west of the prime meridian.

Figure \(\PageIndex{1}\): Lines of Latitude and Longitude (© Djexplo, Wikipedia Commons, CC0 1.0)

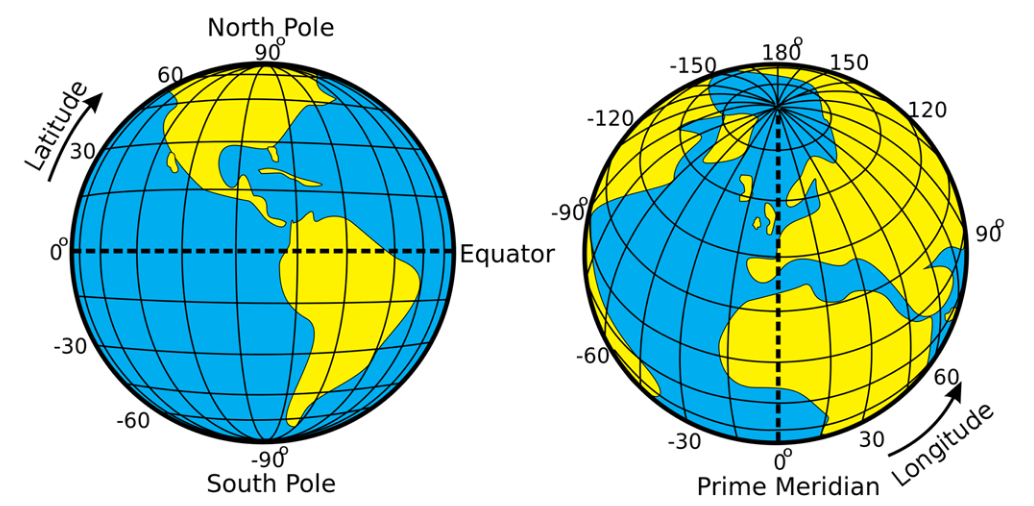
Every place on Earth has a precise location that can be measured with latitude and longitude. The location of the White House in Washington, DC, for example, is located at latitude 38.8977 °N and longitude 77.0365°W. Absolute location might also refer to details like elevation. The Dead Sea, located on the border of Jordan and Israel, is the lowest location on land, dipping down to 1,378 feet below sea level.

Historically, most maps were hand-drawn, but with the advent of computer technology came more advanced maps created with the aid of satellite technology. Geographical Information Service (GIS), sometimes also referred to as geographic information systems,uses computers and satellite imagery to capture, store, manipulate, analyze,manage, and present spatial data. GIS essentially uses layers of information and is often used to make decisions in a wide variety of contexts. An urban planner might use GIS to determine the best location for a new fire station, while a biologist might use GIS to map the migratory paths of birds. You might use GIS to get navigation directions from one place to another, layering place names, buildings, and roads.

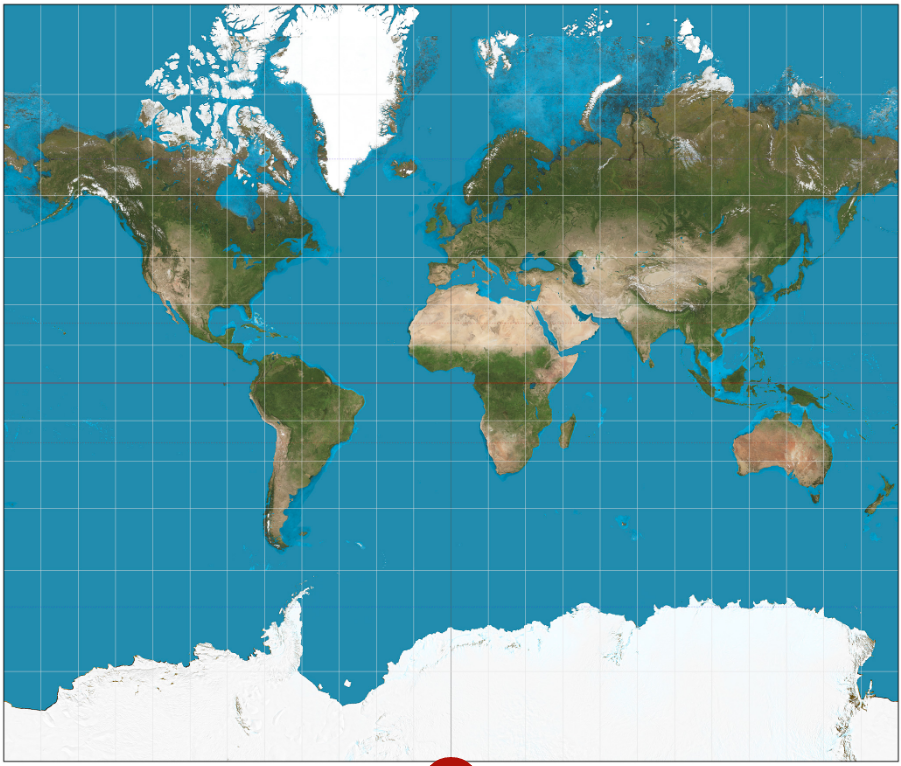
One difficulty with map-making, even when using advanced technology, is that the earth is roughly a sphere while maps are generally flat. When converting the spherical Earth to a flat map, some distortion always occurs. A map projection , or a representation of Earth’s surface on a flat plane, always distorts at least one of these four properties: area, shape, distance, and direction. Some maps preserve three of these properties, while significantly distorting another, while other maps seek to minimize overall distortion but distort each property somewhat. So which map projection is best? That depends on the purpose of the map. The Mercator projection, while significantly distorting the size of places near the poles, preserves angles and shapes, making it ideal for navigation (Figure \(\PageIndex{2}\)).

Figure \(\PageIndex{2}\): Mercator Projection (© Daniel R. Strebe, Wikimedia Commons, CC BY-SA 3.0

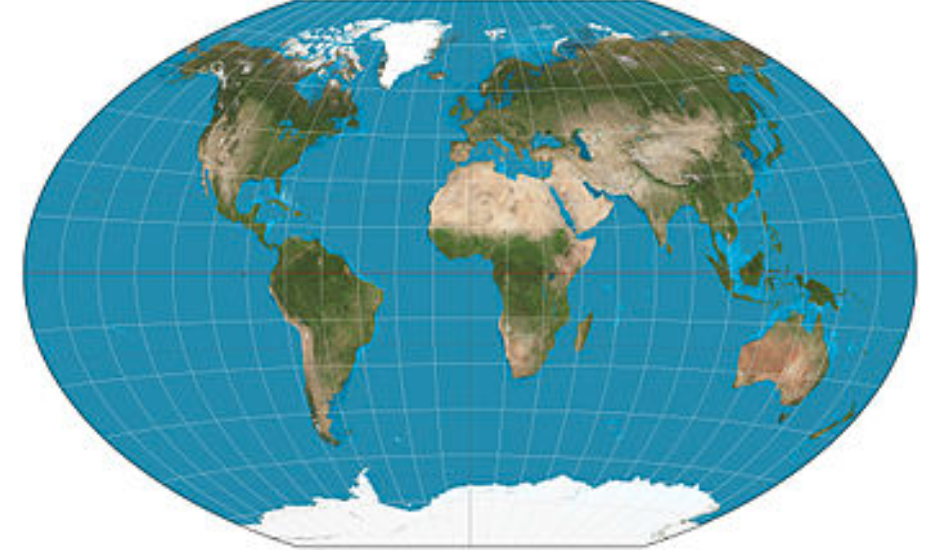
The Winkel tripel projection is so-named because its creator, Oswald Winkel, sought to minimize three kinds of distortion: area, direction, and distance (Figure \(\PageIndex{3}\)). It has been used by the National Geographic Society since 1998 as the standard projection of world maps.

Figure \(\PageIndex{3}\): Winkel Tripel Projection (© Daniel R. Strebe, Wikimedia Commons, CC BY-SA 3.0)

When representing the Earth on a manageable-sized map, the actual size of location is reduced. Scale is the ratio between the distance between two locations on a map and the corresponding distance on Earth’s surface. A 1:1000 scale map, for example, would mean that 1 meters on the map equals 1000 meters, or 1 kilometer, on Earth’s surface. Scale can sometimes be a confusing concept for students, so it’s important to remember that it refers to a ratio. It doesn’t refer to the size of the map itself, but rather, how zoomed in or out the map is. A 1:1 scale map of your room would be the exact same size of your room – plenty of room for significant detail, but hard to fit into your glove compartment. As with map projections, the “best” scale for a map depends on what it’s used for. If you’re going on a walking tour of a historic town, a 1:5,000 scale map is commonly used. If you’re a geography student looking at a map of the entire world, a 1:50,000,000 scale map would be appropriate. “Large” scale and “small” scale refer to the ratio, not to the size of the landmass on the map. 1 divided by 5,000 is 0.0002, which is a larger number than 1 divided by 50,000,000 (which is 0.00000002). Thus, a 1:5,000 scale map is considered “large” scale while 1:50,000,000 is considered “small” scale.

All maps have a purpose, whether it’s to guide sailing ships, help students create a more accurate mental map of the world, or tell a story. The map projection, color scheme, scale, and labels are all decisions made by the mapmaker. Some argued that the widespread use of the Mercator projection, which made Africa look smaller relative to North America and Eurasia, led people to minimize the importance of Africa’s political and economic issues. Just as texts can be critiqued for their style, message, and purpose, so too can maps be critiqued for the information and message they present.

The spatial perspective, and answering the question of “where,” encompasses more than just static locations on a map. Often, answering the question of “where” relates to movement across space. Diffusion refers to the spreading of something from one place to another, and might relate to the physical movement of people or the spread of disease, or the diffusion of ideas, technology, or other intangible phenomena. Diffusion occurs for different reasons and at different rates. Just as static features of culture and the physical landscape can be mapped, geographers can also map the spread of various characteristics or ideas to study how they interact and change.

Relative Location:

the location of a place relative to other places

Absolute Location:

references an exact point on Earth and commonly uses specific coordinates like latitude and longitude

Latitude:

imaginary lines that run laterally, parallel to the equator, around the earth and measure distances north or south of the equator

Longitude:

imaginary lines that circle the earth and converge at the poles, measuring distances east and west of the equator

Geographical Information Science:

also referred to as geographic information systems, or GIS; a program that uses computers and satellite imagery to capture, store, manipulate, analyze, manage, and present spatial data.

Distortion:

changes that occur in area, shape, distance, and/or direction when representing a spherical Earth on the flat surface of a map

Scale:

the ratio between the distance between two locations on a map and the corresponding distance on Earth’s surface

Diffusion:

refers to the spreading of an idea, object, or feature from one place to another